前言
由于个人目前对于计算机视觉有比较大的兴趣,想写一篇关于CNN的文章总结学到的东西,参考花书,以及一些比较权威的视频课。
基本概念
- 卷积 :是对两个实变函数的一种算术运算。
- 卷积神经网络一般是用来处理具有类似网格结构的数据的神经网络,例如时间序列,和图像素数据。
关于时间序列一般公式:
s ( t ) = ( x ∗ w ) ( t ) s(t) = (x*w)(t) s(t)=(x∗w)(t)
星号表示卷积运算。
x:输入,w:核函数,两者会随着t的怪变而改变。
对于二维图像数据:
S ( i , j ) = ( I ∗ K ) ( i , j ) = ∑ m ∑ n I ( m , n ) K ( i − m , j − n ) S(i, j) = (I*K)(i,j) = sum_m sum_nI(m,n)K(i-m, j-n) S(i,j)=(I∗K)(i,j)=m∑n∑I(m,n)K(i−m,j−n)
不同于机器学习系统
- 稀疏交互
- 参数共享
- 等变表示
- 稀疏交互
可以通过使用相对与输入较小的核函数减少参数的数量,从而提高了训练模型的效率。 - 参数共享
一个模型的多个函数使用想用的参数。
传统神经网络:

其中每一个权重都只使用一次。
而卷积运算往往会多次使用权重元素。
3. 等变表示
含义: 如果一个函数满足输入改变,输出也以同样的方式改变这一性质,我们就说他是等变的。
等变表示可以理解为是参数共享引起的。特点是:如果图像a经过函数g向右移动了一个单位变化为b,则那么这种边变换和卷积运算的先后顺序是没有影响的。
- 影响输出单元s的输入单元x1, x2, x3称为s的接受域。
attention: 处在卷积网络更深层中的单元,它们的接受域要比处在浅层的单元的接受域更大。如归网络中还包含池化之类的结构特征,这种效应会加强。(处在更深层中的单元可以间接地链接到全部或大部分输入图像)
池化
- 池化函数使用某一位置的输出总体统计特征来代替网络在该位置的输出,例如最大池化,平均池化,最小池化等等。
- 假设在机器博弈中,一般在训练决策函数的时候,往往会对当天的器具做旋转,翻转操作,当使用pooling层时,棋局真正的进行到了模型匹配状态的时候过滤器会匹配它并在探测单元中引起大的激活,然后无论哪个探测单元激活,最大池化单元都具有大的激活,这样便提高了统计效率。
RGB图像中的垂直边缘和横向边缘
在RGB三维图像中使用卷积核函数。
- 在卷积核的第一层(对应R通道)使用[1, 0 ,-1], [0 ,0 ,0], [0, 0, 0]的卷积核可以得到垂直边缘.
- 可以使用另一个卷积核来计算图像的水平边缘
- 这样输出就会变为 n* n* filter。
单层卷积网络
进行卷积运算之后往往还要加上偏置项,这里的偏置项会加上卷积运算之后结果的每一项,也就是说会进行广播操作。输出的层数决定于卷积核的数量。
- 可以通过过滤器检测图像的不同特征,例如水平边缘线,垂直边缘线等等。
- 关于卷积运算的一些简易的标识符:
假设l层是卷积层则:- f [ l ] = f i l t e r s i z e f^{[l]} = filter space size f[l]=filter size
- p [ l ] = p a d d i n g p^{[l]} = padding p[l]=padding
- s [ l ] = s t r i d e s^{[l]} = stride s[l]=stride
- n c [ l ] = n u m b e r o f f i l t e r s n_c^{[l]} = number space of space filters nc[l]=number of filters 卷积核的数量
- I n p u t : n H [ l − 1 ] ∗ n w [ l − 1 ] ∗ n c [ l − 1 ] Input: n_H^{[l-1]}*n_w^{[l-1]}*n_c^{[l-1]} Input:nH[l−1]∗nw[l−1]∗nc[l−1] 输入的维数
- O u t p u t : n H [ l ] ∗ n w [ l ] ∗ n c [ l ] Output: n_H^{[l]}*n_w^{[l]}*n_c^{[l]} Output:nH[l]∗nw[l]∗nc[l] 输出结果的维数
- n H [ l ] = [ n w [ l − 1 ] + 2 p [ l ] − f [ l ] s [ l ] + 1 ] n_H^{[l]} = [frac{n_w^{[l-1]} + 2p^{[l]} - f^{[l]}}{s^{[l]}}+1] nH[l]=[s[l]nw[l−1]+2p[l]−f[l]+1] 输出的高、宽
- E a c h f i l t e r i s : f [ l ] ∗ f [ l ] ∗ n c [ l − 1 ] Eachspace filter is: f^{[l]}*f{[l]}*n_c^{[l-1]} Each filteris:f[l]∗f[l]∗nc[l−1] 每个卷积核函数
- A c t i v a t i o n s : a [ l ] − > n H [ l ] ∗ n W [ l ] ∗ n c [ l ] Activations: a^{[l]} -> n_H^{[l]}*n_W^{[l]}*n_c^{[l]} Activations:a[l]−>nH[l]∗nW[l]∗nc[l] 激活函数
- A [ l ] − > m ∗ n H [ l ] ∗ n w [ l ] ∗ n c [ l ] A^{[l]}->m*n_H^{[l]}*n_w^{[l]}*n_c^{[l]} A[l]−>m∗nH[l]∗nw[l]∗nc[l]
- 上述:当使用批量梯度下降法求解参数时,假设输入数量是m则由上述式子,也即是说要求m组参数矩阵, 输出即为A[l]
- Weights: f [ l ] ∗ f [ l ] ∗ n c [ l − 1 ] ∗ n c [ l ] f^{[l]}*f^{[l]}*n_c^{[l-1]}*n_c^{[l]} f[l]∗f[l]∗nc[l−1]∗nc[l]
- bias: n c [ l ] n_c^{[l]} nc[l]
深层卷积网络
需要注意的是在卷积层之间,应该注意参数的顺序和大小,这些都可以通过计算而得到。最后的一层输出可以展开为一维向量,同过激活函数得到我们想要的结果。
在构建深层卷积网络的时候需要注意的是:一般每一层卷积过后的宽和高都是减少的,卷积核的数量都是在不断增加的。
CovNet 一般组成为:
- Convluation
- Pooling
- Fully connected
- 池化层
池化层
- Max pooling: 与卷积计算方式十分的相似。
- pooling层可以理解为是采样层,pooling是一个确定的函数,在训练的过程中没有参数是需要学习的,该层更加的偏向于进行采样。
卷积神经网络样例
LeNet -5:(注意神经网络中的层数指的是哪些有权重有参数的网络成数量)
32 * 32 * 5 - > 28 * 28 * 6 (conv1) - > 14 * 14 * 6 (pooling1) (可以将前面看做是一层) - > 10 * 10 * 16 (conv2) - > 5* 5 * 16 (maxpooling) - > 400(fully layer3) - 120 (400个输入,120个输出)需要一个(120, 400)的权重矩阵 - > 84 (fully4) - > softmax得到一个(10 ,outputs)去判断是哪一个数字。
注意:超参数的选择可以参考文献,
the params:
| Activation shape | Activation Size | # parameters | |
|---|---|---|---|
| Input | (32, 32, 3) | 3072 | 0 |
| CONV1 | (28, 28, 8) | 6272 | 208 |
| POOL1 | (14, 14, 8) | 1568 | 0 |
| CONV2 | (10, 10 , 16) | 1600 | 416 |
| FC3 | (120, 1) | 120 | 48001(bias 会以广播的形式加上去) |
| FC4 | (84, 1) | 84 | 10081 |
| Softmax | (10, 1) | 10 | 841 |
通常情况下 : Activation Size 应该缓慢的减少,不应该减的太快。
构建一个好的卷积网络往往需要通过阅读大量的实例积累经验。并不是随意想象出来的,自己构建的效果往往并没有那么好的效果。
为什么使用卷积(优点)
- 相对于传统网络会使用很少的参数。
- parameter sharing
- Sparsity of connections 稀疏连接
- 通过卷积函数的上述性质可以大大的减少参数的使用
卷积神经网络实例
- LeNet - 5(文献)
- AlexNet 使用了relu激活函数
- VGG -16(优点:简化了神经网络模型)过滤器数量倍数增加
ResNet 残差网络
使用残差网络的原因是,当神经网络模型的层数越深的时候往往,训练误差不会减少,而残差网络网可以决绝这一问题。
- 当采用深层神经网络的时候,使用训练集训练神经网络的能力下降,而当采用的残差网络的时候就不必太担心这个问题了。
- a [ l + 2 ] = g ( z [ l + 2 ] + a [ l ] ) = g ( w [ l + 2 ] a [ l + 1 ] + b [ l + 2 ] + a [ l ] ) = ( 当 w , b 为 0 时 ) = g ( a [ l ] ) a^{[l+2]} = g(z^{[l+2]}+a^{[l]})=g(w^{[l+2]}a^{[l+1]}+b^{[l+2]}+a^{[l]})=(当w,b为0时)=g(a^{[l]}) a[l+2]=g(z[l+2]+a[l])=g(w[l+2]a[l+1]+b[l+2]+a[l])=(当w,b为0时)=g(a[l]) 即便中间右额外的两层但和没有这两层是一样的。
1x1的卷积核能够做什么
- 对于二维图像来说使用一个人1*1的卷积核,相当于是将该卷积核上的值分别乘以输入,
- 对于一个多通道的图像来说就是将一个卷积核上的所有值乘以输入,这其实相当于是一个全连接网络,结果可以通过relu函数计算结果,作为输出。输出可以作为和输入相同宽和高的一个过滤器。
- 这种结构也被称为是网中网结构

- 用途:1.通道数太大 用来减少计算量, 2. 用来为输入增加非线性性。
inception network

上述便是一个简单地inception network 实例。
- 计算成本(考虑5*5)

计算该输出需要进行的乘法次数为: (28 * 28 * 32) * (5 * 5 * 192),前者是输出单元数,后者是每个卷积核的大小。
上述结果为1.2亿通过,通过1 * 1的卷积核可以缩小计算量。 - Using 1x1 convolution

该神经网络的中间层可以称作为是瓶颈层(中间小两头大),总的计算层本也大大的减少了。
- inception network的用途就是,当你不知道在网络结构中使用哪种构件时,就可以用这种方式,他会采用所有的方式。
- 总结: 1x1函数怎么生成瓶颈层的,减少计算成本。
使用开源的实现方案
可以通过开源网站,使用别人已经成熟的论文,比如GitHub里面。一方面可以节省时间,另一面可以通过别人已经比较成熟的代码快速的学习到新的知识。
- cmd命令:clone git +url.
- 另一个好处是一般开源程序都是训练好,为我们的二次开发节省了时间。可以直接的对这些网络进行迁移学习。
- 而对于研究者-> github.
迁移学习
- 概述,在别人已经训练好的神经网络的权重作为自己训练的初始数据。
- 当自己的训练的数据比较少的时候,可以采用冻结部分的网络层结构构建新的网络。
- 改变网络输出部分,改用我们想要的那种结果。
- 当数据量很多的时候,可以在原本网络的基础上,以训练好的权重作为随机初始化数据,改变输出为我们想要的,然后继续进行训练。
- 这就是所谓的迁移学习。
数据增强
对于计算机视觉来讲数据量太少往往会成为一个大问题。
数据增强的一些操作。
- 镜像翻转
- 随机裁剪
- 旋转
第二类:
- 色彩变化
- 可以通过增加某些通道值,或减少某些通道的值,带来色彩上的变化。
 引述:PCA色彩增强。
引述:PCA色彩增强。 - 一般情况下可以使用计算机的部分线程去做图像的失真处理(数据增强),另一部分线程用于深度学习的训练。
目标定位
目标定位首先需要了解的是将图像内对象的匪类问题,
- 分类:输入一张图像,经过卷积操作之后获得一个特征向量,与我们想要得到的结果构成成本函数,经过梯度下降法训练权重。
- 假设一张图片上有行人,汽车,自行车,背景四个对象那么上面的输出也应该为四位。
假设现在需要让网络具有定位功能需要做的是改变神经网络结构,需要在输出结果加上四个结果,bx, by, bw, bh.用来确定检测对象的边框。
网络的输出结果可以定义为:
y
=
[
p
c
b
x
b
y
b
h
b
w
c
1
c
2
c
3
]
y = left[ begin{matrix} p_c \ b_x\ b_y \ b_h\ b_w \ c_1 \ c_2 \ c_3 \ end{matrix} right]
y=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡pcbxbybhbwc1c2c3⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤
pc:是否检测到了除背景外的对象,b_x:是用来检测图像边框的坐标位置。
(b_x, b_y)中心坐标,b_w,b_h为边框的长宽。
c_1, c_2, c_3用来标记是哪个对象,对象标记到的用1表示,否则用0。
需要注意的是当pc=0时,也就是说没检测到对象,计算cost function时需要忽略后面所有的结果。
- 如果是一张人脸图像需要做的是检测要眼角的位置,需要做的是修改神经网络的输出结果为眼角的位置。
Sliding windows decection
选择适当大小的边框作为滑动窗口,用方框标记的图像作为卷积网络的输入,判断结果是否有想要的对象,经过一次查找后,没有找到,再换用跟大的边框继续上述操作。
缺点:计算成本过高,因为裁剪了很多的正方形,并且需要将每个正方形单独的通过卷积神经网络的运算,
- 步长的选择:步长太长容易忽略要检查的对象,步长太小的话将会面对很大的数据,将他们再通过卷积神经网络以为着很高的计算成本。
通过卷积的方式减少计算成

如上图:中第一层要原本卷积之后通过两个全连接层输出一个y。现在假设是需要将输出改为每个对象的概率,那么需要对第一层的网络做修改。
而,第二层中使用400个卷积核获取1x1x400的输出,其实相当于是在原本的输出的基础上对每个点做线性变换。
个人理解:第一层的网络中有16通道的特征每一层对应一种线性变换,直接将他们拉平的话旨在突出图像的某个区域对于分类的贡献。
而第二层使用的是图像的不同函数映射,旨在突出图像的主导作用,而这正是我们需要的。
卷积实现滑动窗口

假设14x14是要识别的边框,经过卷积运算可以知道他是什么对象的概率。
28x28可以当做是原始图像那么经过相同的操作输出的结果可以看做和平滑的结果是一样的。
存在问题:窗口边框的定位不精确。
如何更精确的确定边框的位置
YOLO算法:可以解决边框不精确的问题。(you only look once)
方法:
- 给出一个图片
- 将图片以网格的形式划分成若干个块。
- 将分块将分块图像分别应用之前分类和定位算法。
- Labels for training
For each grid cell:
y = [ p c b x b y b h b w c 1 c 2 c 3 ] y = left[ begin{matrix} p_c \ b_x\ b_y \ b_h\ b_w \ c_1 \ c_2 \ c_3 \ end{matrix} right] y=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡pcbxbybhbwc1c2c3⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤
与 y ^ hat{y} y^构成成本函数。
100 * 100 * 3 - > convnet - > 3 * 3 * 8(取决于想要分成的块数)
对于一个网格中只含有一个对象的图像是没有问题的。对于每个目标物,会先判断他的中心坐标点是属于哪个网格,所以即使目标物包含在多个网格中也不会产生冲突。
注意: - 该算法与之前学习的目标定位算法很相似,它的输出结果会变得更加的精确,而不会受限于窗口的步长。
- 这个算法是通过卷积实现的而不是对每个网格分别使用定位算法,将会有大量的参数共享解决计算成本。
个人理解:YOLO可以看做使用卷积的方法实现一种滑动(输入数据无重叠滑动)。并且以目标物中心坐标为准则判断是否含有目标对象。
对比之前讲的用卷积的方式实现滑动有如下不同 - 之前讲的滑动方法是以整个图像都在图像中为基础的,也就是说方块选取的大小,以及步长对图像识别的准确率有很大影响。
- yolo降低了这种因素,以目标中心坐标为主导依据。
- yolo的优点就是计算速度非常的快,可以应用于实时的图像上去。
关于yolo的细节处理
- 如何指定边界框,以左上角为原点,向右为x轴,向下为y轴,bx用来表示目标物中心占据x轴的比例,by用俩表示中心点占y轴的比例。bh表示目标物的高度占方格总高度的比例,bw表示目标物的宽度占方格宽度的比例。
- 也就是说这些坐标是相对于方格来表示的。值得注意的是bh,bw是可以大于1的也就是说宽度或则高度大于一个方格。
交并比
对边框的选择做出评分。 如图所示正方形为目标物包含的边框,长方形为尝试给出的边框,用他们的交集比上并集就可以最为一个评估函数。可以设置一个阀值,一般在计算机视觉中Lou的值为0.5,显然Lou设置的越高精确度就越高。
如图所示正方形为目标物包含的边框,长方形为尝试给出的边框,用他们的交集比上并集就可以最为一个评估函数。可以设置一个阀值,一般在计算机视觉中Lou的值为0.5,显然Lou设置的越高精确度就越高。
Lou的设置初衷:是作为一个评估方法来判断定位算法是否准确,也可以认为是两个边界框重叠度的一个度量。
非极大值抑制(Non-max suppression example)
选择lou值最大边框为我们想要的边框。
算法细节:
输出结果:Each output prediction is:
[
p
c
b
x
b
y
b
h
b
w
]
left[ begin{matrix} p_c \ b_x\ b_y \ b_h\ b_w \ end{matrix} right]
⎣⎢⎢⎢⎢⎡pcbxbybhbw⎦⎥⎥⎥⎥⎤
设置pc的值为:value,小于value的值将被抛弃。
当有一些剩余的方框。
- 选择pc值最大的那个结果作为预测值。
- 使用上一步的预测值,丢弃所有与上一步结果有多层叠的边框。
Face verification and face recognition
Verification
- input image, name/ID
- Output whether the input image is that of the claimed person
Recognition
- Has a database of K Persons
- Get an input image
- Output ID if the image is any of th any K persons (or no recognized)
- 一对多问题,数据库越多,要求验证的结果就越精确。
Learning a ‘similarity’ function
- d(img1, img2) = degree of differnece between images
- if d(img1, img2) <= τ tau τ same
- else: different

如果没有人足够相似就会判断他不再数据库中。
另外一个好处是当数据库中新加入一个成员之后,程序还是可以正常的进行下去。
Siamese network
x
(
1
)
=
>
c
o
n
v
1
=
>
c
o
n
v
2
=
>
c
o
n
v
3
=
>
F
C
=
=
>
y
(
1
)
x^{(1)}=>conv1 =>conv2 =>conv3 => FC == >y^{(1)}
x(1)=>conv1=>conv2=>conv3=>FC==>y(1)
y
(
1
)
=
f
(
x
(
1
)
)
y^{(1)} = f(x^{(1)})
y(1)=f(x(1)), we can consider this as “encoding” of x(1)
- we can also get y ( 2 ) = f ( x ( 2 ) ) y^{(2)} = f(x^{(2)}) y(2)=f(x(2))
- so degree of difference os image is d ( x ( 1 ) , x ( 2 ) ) = ∣ ∣ f ( x ( 1 ) ) − f ( x ( 2 ) ) ∣ ∣ d(x^{(1)}, x^{(2)}) = ||f(x^{(1)}) - f(x^{(2)})|| d(x(1),x(2))=∣∣f(x(1))−f(x(2))∣∣
How to train this network?
- the parameters of neuro network is same
- Parameters of NN define an encoding f ( x ( i ) ) f(x^{(i)}) f(x(i))
- Learn parameters so that:
- if x ( i ) , x ( j ) x^{(i)}, x^{(j)} x(i),x(j)are the same person, ∣ ∣ f ( x ( i ) ) − f ( x ( j ) ) ∣ ∣ 2 ||f(x^{(i)}) - f(x^{(j)})||^2 ∣∣f(x(i))−f(x(j))∣∣2 is small
- if x ( i ) , x ( j ) x^{(i)}, x^{(j)} x(i),x(j)are the different person, ∣ ∣ f ( x ( i ) ) − f ( x ( j ) ) ∣ ∣ 2 ||f(x^{(i)}) - f(x^{(j)})||^2 ∣∣f(x(i))−f(x(j))∣∣2 is large
- by BP algorithm adjust parameters
Detail: How to get cost function?
picture:
- we want ∣ ∣ f ( A ) − f ( P ) ∣ ∣ 2 < = ∣ ∣ f ( A ) − f ( N ) ∣ ∣ 2 ||f(A) - f(P)||^2<=||f(A)-f(N)||^2 ∣∣f(A)−f(P)∣∣2<=∣∣f(A)−f(N)∣∣2
- be equivalent to ∣ ∣ f ( A ) − f ( P ) ∣ ∣ 2 − ∣ ∣ f ( A ) − f ( N ) ∣ ∣ 2 ||f(A)-f(P)||^2 - ||f(A)-f(N)||^2 ∣∣f(A)−f(P)∣∣2−∣∣f(A)−f(N)∣∣2
通过上述表达式可以发现是两个方程式相减的结果为了防止网络结果退化,需要加入一个超参数使网络结构学习的更好。
Summary:
∣
∣
f
(
A
)
−
f
(
p
)
∣
∣
2
−
∣
∣
f
(
A
)
−
f
(
w
)
∣
∣
2
+
m
a
r
g
i
n
<
=
0
||f(A)-f(p)||^2-||f(A)-f(w)||^2+margin<=0
∣∣f(A)−f(p)∣∣2−∣∣f(A)−f(w)∣∣2+margin<=0
前者要远小于后者的结果。
Loss Function:
- given 3 image A,P,N。
- ζ ( A , P , N ) = m a x ( ∣ ∣ f ( A ) − f ( p ) ∣ ∣ 2 − ∣ ∣ f ( A ) − f ( w ) ∣ ∣ 2 + m a r g i n , 0 ) zeta(A,P,N) = max(||f(A)-f(p)||^2-||f(A)-f(w)||^2+margin, 0) ζ(A,P,N)=max(∣∣f(A)−f(p)∣∣2−∣∣f(A)−f(w)∣∣2+margin,0)
- 当方程式是小于的时候不用在意它是负的多少。
推广:
J
=
∑
i
=
1
m
ζ
(
A
(
i
)
,
P
(
i
)
,
N
(
i
)
)
J=sum_{i=1}^{m}zeta(A^{(i)}, P^{(i)}, N^{(i)})
J=i=1∑mζ(A(i),P(i),N(i))
Traing set: 10k pictures of 1k persons
for A,P we need get same picture.
Choosing the triplets A,P,N
During training if A,P,N are chosen randomly
d(A,P) +
α
alpha
α <= d(A, N) is easily satisfied.
- so by this equation we will learn small knowledge.
- Choose triplets that’re ‘hard’ to train on.
- while ζ ( A , P ) i s v e r y s i m m e r w i t h ζ ( A , N ) zeta(A,P) is very simmer with zeta(A,N) ζ(A,P)isverysimmerwithζ(A,N) so the NN will change parameters obviously.
Face verification and binary classification
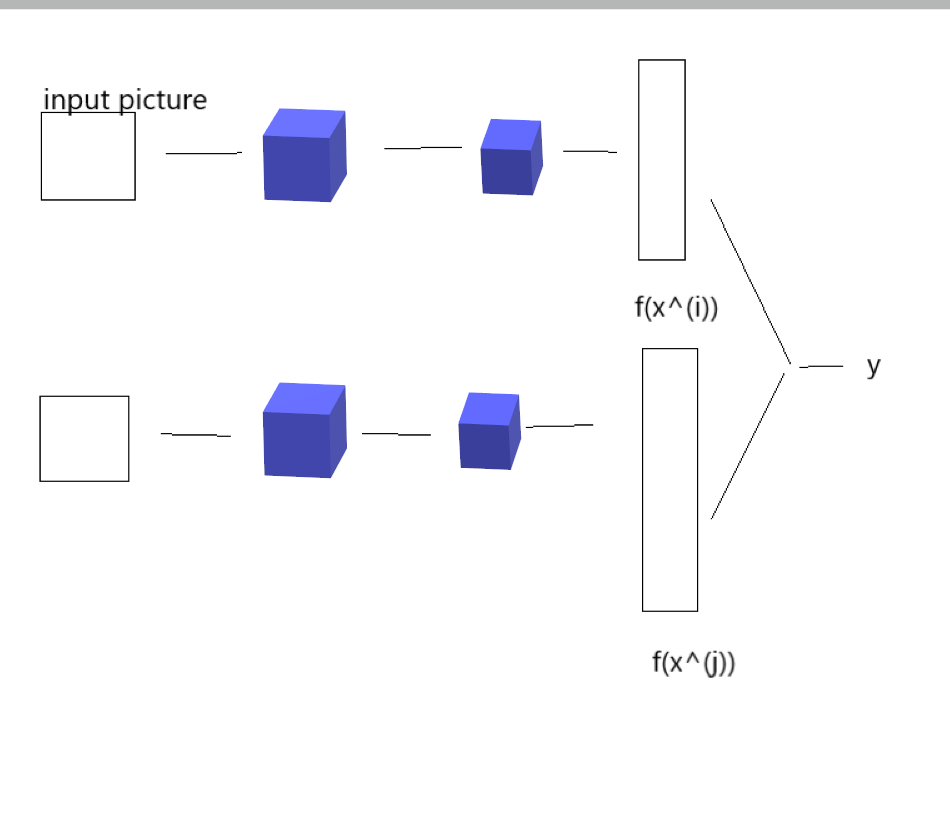
-
if
x
(
i
)
x^{(i)}
x(i) and x^{(j)} is same people y = 1, else y= 0。
y
^
=
σ
(
∑
k
=
1
n
∣
f
(
x
k
(
i
)
)
−
f
(
x
k
(
j
)
)
∣
+
b
)
hat{y} = sigma(sum_{k=1}^{n}|f(x^{(i)}_k) -f(x^{(j)}_k)| + b)
y^=σ(k=1∑n∣f(xk(i))−f(xk(j))∣+b)
下标k为向量的第k个元素。也就是两种编码逐个元素的差的绝对值的和。
最后
以上就是爱笑眼睛最近收集整理的关于计算机视觉基础RGB图像中的垂直边缘和横向边缘的全部内容,更多相关计算机视觉基础RGB图像中内容请搜索靠谱客的其他文章。








发表评论 取消回复