关于DFT变换含义、公式和具体形式

原文地址：http://blog.sina.com.cn/s/blog_7853c3910102v9wd.html

这篇文章从实际工程应用的角度，记录一下如何计算，关于公式、变形和应用。

维基百科上的DFT公式：
对于N点序列，它的离散傅里叶变换（DFT）为

有时候也能见到等式右边的系数不是1，而是1/N或者1/√N，最常用的还是系数为1的，只要保持“DFT变换”和“IDFT（DFT反变换）变换”系数一致就好。

我们知道：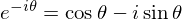

假设 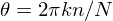, 那么公式变形为：

进一步：

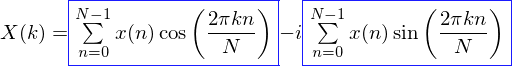
所以其实DFT变换就是两个“相关（correlation）”操作，一个是与频率为K的COS序列相关，一个是与频率为K的SIN序列相关，然后两者叠加就是与频率K的正弦波相关的结果，如果赋值很大，就表明信号包含频率为K的能量很大。

这里简单举个简单例子，假设序列x(n)=[1 0 -1 0],N=4。

k=0，那么：

X(0)=[1 0 -1 0]*[1 1 1 1]’-i[1 0 -1 0]*[0 0 0 0]’

=0+i*0

也就是说其直流（DC）分量为0

k=1,那么：

X(1)= [1 0 -1 0]*[1 0 -1 0]’-i[1 0 -1 0]*[0 1 0 -1]’

      = 2-i*0

也就是说其一次谐波分量值很大，并且是和COS波形最相似（SIN分量能量为0）

k=2那么：

X(2)= [1 0 -1 0]*[1 -1 1 -1]’-i[1 0 -1 0]*[0 0 0 0]’

      = 0-i*0

也就是说其二次谐波分量值为0.

X(3)= [1 0 -1 0]*[1 0 -1 0]’-i[1 0 -1 0]*[0 -1 0 -1]’

      = 2+i

嗯？？怎么三次谐波分量居然那么大，哦，原来是采样频率不够大，其三次谐波根本就恢复不出来。

这里我要专门研究一下关于角度的问题，还是和上面类似的例子，假设序列x(n)=[ √2/2  -√2/2  -√2/2  √2/2],N=4 ，k=1,那么：

X(1)= [ √2/2  -√2/2  -√2/2  √2/2 ]*[1 0 -1 0]’-i[ √2/2  0 -√2/2 0]*[0 1 0 -1]’

      = √2+i*√2

也就是说一次谐波的相位是PI/4，而不是-PI/4。有时候应用DFT的时候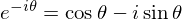 里面第二项的”-“号容易被忽略。另外函数ATAN2的含义是：

 ATAN2（Y坐标,X坐标）

但是”-“号被忽略其实也不是大问题，只是计算出来的虚部符号相反，并不影响幅值（magnitude），而相位会相反，只要保证后续处理一致，那么相位和标准DFT定义相反也没关系。我们的设计当中就是定义的和标准DFT相位相反。

最后

以上就是清爽蜻蜓为你收集整理的关于DFT变换含义、公式和具体形式的全部内容，希望文章能够帮你解决关于DFT变换含义、公式和具体形式所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。