5GNR漫谈17：OFDM载波频偏估计（CFO）

发射机的载波Ftx和接收机的载波Frx，是由各自射频硬件电路上的晶振源提供，由于是两个独立的物理器件，不可避免的存在频率上的偏差。频率偏差，会造成调制数据相位上的旋转，在接收端必须对频偏进行纠正。
在漫谈15中，我们已经介绍了OFDM调制的本质，是两级的IQ调制，第二级IQ调制，将第一级得到的复信号，实部和虚部分别在I路和Q路上发射出去。基带的IQ两路序列为x(n)的实部和虚部：

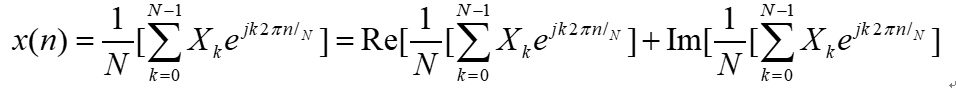
为方便表达，通常将第二级IQ调制发射出去的射频信号表达为复等效形式：

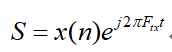
Ftx为发射载波频率，相当于把基带的x(n)信号，搬到Ftx频点上发射出去。在接收端，采用与Ftx相同的载波频率将x(n)搬到基带，于是有

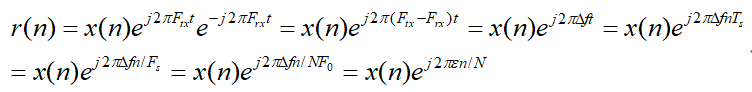
上式推导过程中Fs为采样频率，F0为子载波间隔，ε为归一化频偏误差。许多文献只给出上式中的最终结果，没有给出推导过程，让人摸不着头脑。ε通常又再细化为整数部分和小数部分，整数部分相当于调制数据受频偏影响，跑到了附近的子载波位置上，此时调制数据还保持正交性，只是相位旋转到别的星座图上，小数部分则会破坏调制数据的正交性。
先来估计小数倍频偏，补偿数据，根据补偿小数倍频偏后的数据，再估计整数倍频偏，再补偿整数倍频偏，消除所有频偏影响。
观察上式，我们发现，接收序列相位会随着单位时间增加偏转2πε/N的角度。如果发送一组序列在时间上有前后部分相同，那么根据后一部分的数据相对于前一部分数据的旋转角度大小，再除于时间上的距离，不就求得ε了吗？正是如此。OFDM符号可以采用重复的循环前缀CP来求频偏，也可以在协议设计时，在时域上发送相同的OFDM符号训练序列，用来估计频偏，比如wifi协议的长preamble和短preamble，会重复发送。
假如两段重复样点间的距离为D，重复样点长度为L，则有延时相关：

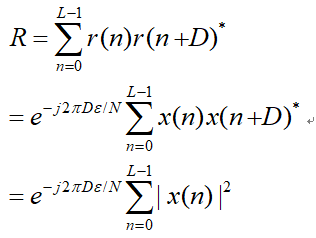
从而得到归一化载波频率偏差的估计值为：

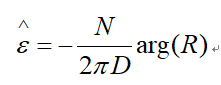
其中arg()为求角度。通常D的长度等于一个OFDM符号的长度N，所以有：

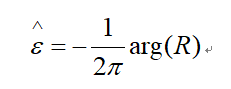
而arg()运算的角度范围为（-π, π）,所以ε范围为（-0.5，0.5），也即，采用一个OFDM符号长度的重复距离估计的频偏只能是小数倍频偏。而如果令N=KD,K>2的正整数，则估计的范围为（-0.5K，0.5K），此时，不仅可以估计小数倍频偏大小，还可以估计整数倍频偏大小。N=KD的意义，在OFDM符号长度为N的距离内，有K个长度为D的重复序列。这正是WiFi协议采用OFDM调制时preamble设计的思想。下图中WiFi short preamble重复了10次发射，long preamble重复了2次发射，都是为了更好的对频偏进行估计。

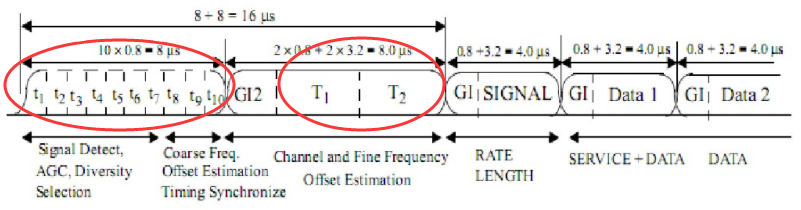
我们发现，采用训练序列的方法，训练符号会占用所有时间和频域上的资源。这种方法只会在系统初始接入的时候采用，所以训练序列只会在帧头位置发射。
我们来看看另一种频偏估计的方法，这种方法在OFDM符号payload频域数据里面插入导频，根据导频数据来估计频偏大小，这样既可以提高系统的资源利用率，又可以跟踪频偏的变化。因为频偏误差是估计出来的，不可能与真实的频偏大小刚好一致，总是会残留一定的大小。而随着时间的积累，残留频偏会使得调制数据发生足够大的相位误差，造成解调误码。
这种方法首先是捕获阶段，然后是跟踪阶段。
记归一化的载波频率为

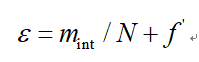
则有对接收到数据补偿小数倍频偏后的FFT:

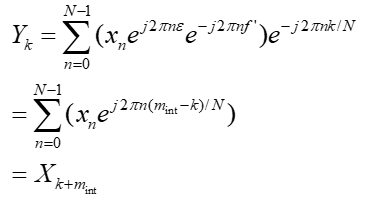
即，整数倍频偏对数据的影响，相当于频域数据位移了整数位，又因为OFDM符号首尾是CP循环前缀的，因此这种频域数据的位移是循环的。
通常导频数据是确定的，会利用相关性很好的序列来充当导频，插入到OFDM频域paylaod数据位置。当存在整数倍频偏大小时，接收频域数据会整体循环移位。此时，我们采用本地生成的导频序列，与接收频域序列滑动后提取的导频数据做相关，取得最大相关峰值的序列所滑动的距离，即为归一化整数倍频偏大小。
用公式来表示为：

而我们知道，定时误差，会给频域数据带来相位偏转，所以如果采用定时有误差的频域数据和本地导频数据做滑动相关求峰值，必然会带来峰值的偏移，所以，首要的前提是要对OFDM符号的起始做到精确的定时。
一种消除定时误差而引起相关峰值移位的方法，是采用差分检测法。这种方法不直接采用本地导频序列与接收到的频域数据滑动找导频序列做相关，而是先采用同一个OFDM符号内两个相邻导频位置上的数据取共轭乘，消除了定时相位偏差，再与本地相同位置的导频共轭乘的结果做滑动相关，求峰值。其理论依据很简单，根据傅立叶变换的性质我们知道，假如有定时误差影响，相当于傅立叶变换有个时延t的影响，对于同一个OFDM符号频域数据，其影响是相同的，两个导频数据取共轭乘，可以消除这个共同的时延影响。差分检测表达式为：

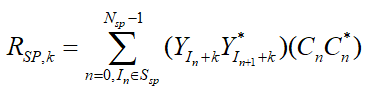
然后用相同的方法求角弧度再求取归一化整数频偏值。
求得整数倍频偏后，补偿数据，然后再对残余频偏进行跟踪。残余频偏通常很小，只有在足够长的时间内积累，调制数据才会形成明显的相位误差。通常会采用残余频偏造成的导频在时长间隔D个OFDM符号周期内相位旋转大小来估计残余频偏。如果仅用两个相邻的OFDM符号，此时相位旋转的角度很小，同时系统又有噪声的存在，在角度没有拉开的情况下，估计的残余频偏会不准确。

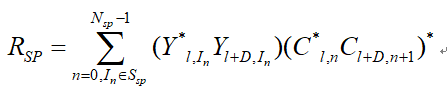
再由上式求取相位偏移值，求取归一化残余频偏大小。
将求取的残余频偏值补偿接收数据，获得更精码的解调数据。

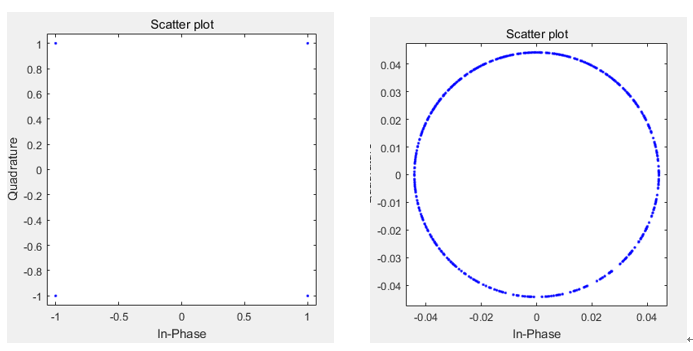
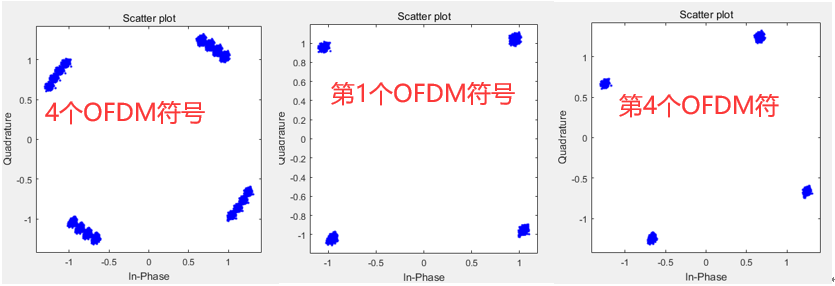
下图是残余归一化频偏为0.0267时的接收数据相信旋转图，从图中可以看到，虽残余频偏很小，但是随着时间的积累，数据的相位旋转影响还是挺大的。

上面介绍了频偏估计的方法，对于LTE或者NR来说，都可以用到以上的各种方法，或者对以上的方法稍微加以改进。比如在小区搜索阶段，可以采用本地PSS时域序列与接收到的PSS时域序列做相关得到相关序列，如果存在频偏，则相关序列的相位误差是随着时间逐点累加的。此时可以把相关序列平均分为前后两份，将前后两个序列取共轭乘，并求取平均相位差，即可知道频偏在半个OFDM符号的时间内累积了多少相位差，进而根据这个相位误差值和时长求得频偏值大小。这是粗频偏。而对于细频偏，可以对SSS序列在频域上求相关，获取更精确的频偏误差。
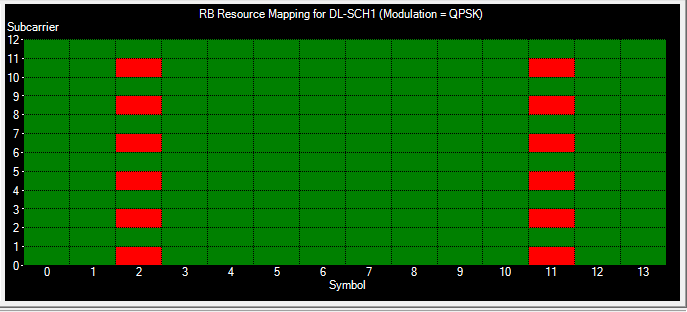
而在解调数据阶段，可以采用导频序列，采用上述的方法，对频偏进行估计和跟踪。NR有多种导频的发送方式，下图是其中一种。

以上介绍了OFDM调制系统频偏估计方法，对于非OFDM调制系统，比如单载波的MSK、DPSK、QAM等调频或者调相系统，频偏估计的方法是不一样的，后面再介绍。

喜欢文章，请加公众号，获得代码、资料：

最后

以上就是舒服鸵鸟为你收集整理的5GNR漫谈17：OFDM载波频偏估计（CFO）的全部内容，希望文章能够帮你解决5GNR漫谈17：OFDM载波频偏估计（CFO）所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。