图之最短路径之迪杰斯特拉算法

104 阅读 0 评论 69 点赞

我是靠谱客的博主虚拟马里奥，最近开发中收集的这篇文章主要介绍图之最短路径之迪杰斯特拉算法，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

一般最短路径算法有迪杰斯特拉算法和弗洛伊德算法，对于有负权值的需要使用弗洛伊德算法，这里主要讲解迪杰斯特拉算法

1.算法思想

设G=(V,E)是一个带权有向图，把图中顶点集合V分成两组，第一组为已求出最短路径的顶点集合（用S表示，初始时S中只有一个源点，以后每求得一条最短路径 , 就将加入到集合S中，直到全部顶点都加入到S中，算法就结束了），第二组为其余未确定最短路径的顶点集合（用U表示），按最短路径长度的递增次序依次把第二组的顶点加入S中。在加入的过程中，总保持从源点v到S中各顶点的最短路径长度不大于从源点v到U中任何顶点的最短路径长度。此外，每个顶点对应一个距离，S中的顶点的距离就是从v到此顶点的最短路径长度，U中的顶点的距离，是从v到此顶点只包括S中的顶点为中间顶点的当前最短路径长度。

应用场景：我们时常会面临着对路径选择的决策问题，例如在中国的一些一线城市如北京、上海、广州、深圳等，一般从A点到到达B点都要通过几次地铁、公交的换乘才可以到达。

2.例子详解

资料摘自：http://www.cnblogs.com/biyeymyhjob/archive/2012/07/31/2615833.html

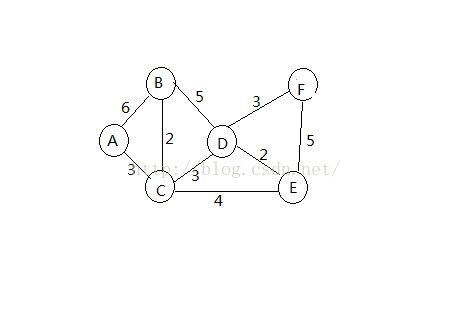
3.迪杰斯特拉算法代码

思路：从某个顶点开始，找其相邻顶点的最短边，将其相邻顶点加入到已访问顶点中，还要从前边已经访问顶点中看是否存在到当前顶点的更短路径，这样就找到当前顶点的最短路径，当当前顶点走到尽头，要进行检查，是否还有未被访问的顶点，找到其与相邻的已被访问顶点T的最小边，则从起点经T到当前顶点即为其最短路径

代码：

import java.util.ArrayList;
import java.util.Scanner;

public class Main {

	public static void main(String[] args) {
		Scanner sc=new Scanner(System.in);
		String line=sc.nextLine();
		String[] str=line.split(" ");
		int n=str.length;
		int[][] matrix=new int[n][n];
		for(int i=0;i
   
   
    
    "+str[row];
		ArrayList
    
    
     
      list=new ArrayList<>();//用于保存访问过的顶点
		list.add(row);
		for(int i=1;i
     
     
      
      ");
					if(k==pre)break;
				}
				sb.append(str[row]);
				visited[row]=1;
				list.add(row);
				path[row]=sb.toString();
				
		}
		//找出未被访问的顶点，寻找其最短路径
		for(int x=1;x
      
      
       
       "+str[x];
			}
		}
		//输出起始顶点到每一个顶点的最短路径以及路径长度
		for(int z=0;z
       
        
 
 
 
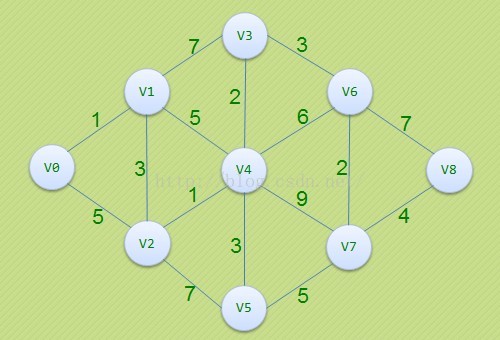
 输入：
 v0 v1 v2 v3 v4 v5 v6 v7 v8
 0 1 5 65535 65535 65535 65535 65535 65535
 1 0 3 7 5 65535 65535 65535 65535
 5 3 0 65535 1 7 65535 65535 65535
 65535 7 65535 0 2 65535 3 65535 65535
 65535 5 1 2 0 3 6 9 65535
 65535 65535 7 65535 3 0 65535 5 65535
 65535 65535 65535 3 6 65535 0 2 7
 65535 65535 65535 65535 9 5 2 0 4
 65535 65535 65535 65535 65535 65535 7 4 0
 输出：
 v0->v0 0
 v0->v1 1
 v0->v1->v2 4
 v0->v1->v2->v4->v3 7
 v0->v1->v2->v4 5
 v0->v1->v2->v4->v5 8
 v0->v1->v2->v4->v3->v6 10
 v0->v1->v2->v4->v3->v6->v7 12
 v0->v1->v2->v4->v3->v6->v7->v8 16