[数字技巧]子集问题（寻找给定集合的所有子集）

　　我们定义该问题如下：

　　给定一个集合C，找出所有的集合C'，使得C'包含于C。

一、无重复元素的集合

　　我们首先来考虑一种简单的情形，C中的数都是各不相同的，这就意味着所产生的子集不会有重复的。

　　直观来说，求一个集合的子集，无非就是对每个元素进行枚举，枚举两种状态”选“还是”不选“。例如，对一个集合C，当对cur这个位置的元素进行枚举时，对剩余的元素可以递归调用这个枚举的过程，当cur为数组长度n时，代表枚举结束。

　　子集的解空间又叫子集树，其叶子节点所代表的状态即为所有的子集。例如，集合{1,3,5}，其子集树如下所示：

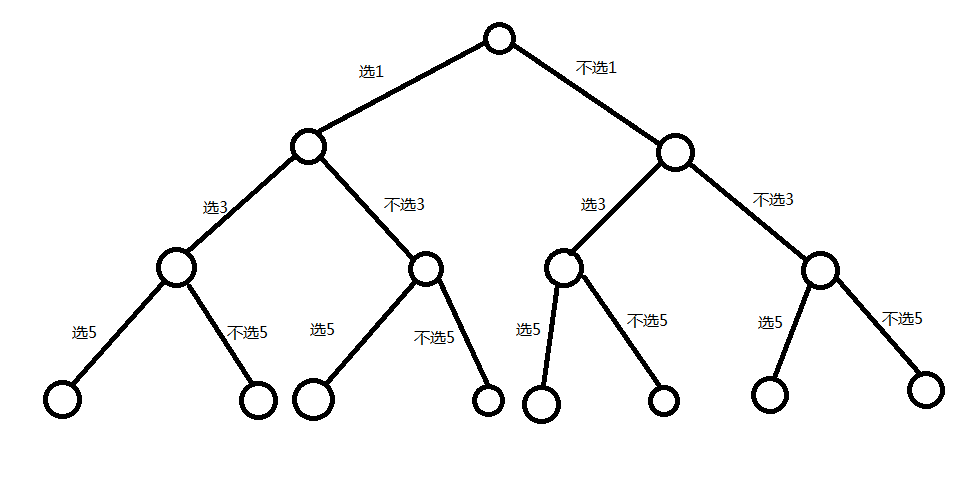
　　如上图所示，共有8个叶子节点，代表8个子集，有了子集树，要求出所有的子集，显然就是一个二叉树的先序遍历问题了，这里我们要设置一个与原数组一样大的标志数组，来标志当前位置”选“还是”不选“，因此，这种方法又叫”位向量法“，代码如下：

#include <stdio.h>
#include <stdlib.h>

int n;
int A[20];
int B[20];

void print_subset(int n, int* B, int cur)
{
    if(cur == n)
    {
        for(int i = 0; i < cur; i++)
            if(B[i]) printf("%d ", A[i]);        // 打印当前集合
        printf("n");
        return;
    }
    B[cur] = 1;                                // 选第 cur 个元素
    print_subset(n, B, cur+1);
    B[cur] = 0;                                // 不选第 cur 个元素
    print_subset(n, B, cur+1);
}

int main()
{
    scanf("%d",&n);
    for(int i=0; i<n; i++)
        scanf("%d",&A[i]);

    print_subset(n,B,0);
    system("Pause");
    
    return 0;    
}

　　另一种有趣的构造子集的方法叫”增量构造法“，顾名思义，这种做法是一种增量式的做法，例如，对集合{1,3,5}，首先确定第一个元素为1，这就是一个子集，然后再这个基础上决定是不是增加3，或者5，形成另外两个子集{1,3},{1,5}，{1,3}再可以决定是不是要继续增加5，而{1,5}中5已经到了最后，因此不能再添加，同样，可以确定第一个元素为2，重复上述步骤。注意，这里集合是定序的，以防止重复。下图给出了使用”增量构造法“对{1,3,5}进行子集搜索的子集树。

　　

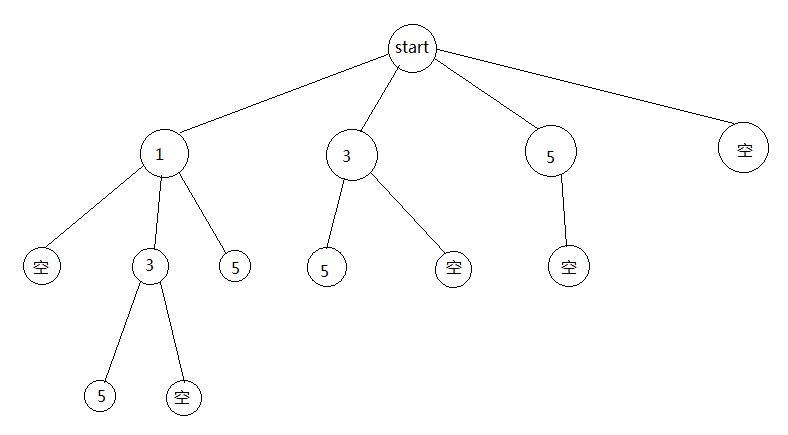
　　下面我们给出使用”增量构造法“的子集生成代码：

//增量构造法

#include <stdio.h>
#include <stdlib.h>

int n;
int A[20];
int B[20];

void print_subset(int n, int* A, int cur);

int main()
{
    scanf("%d",&n);
    for(int i=0; i<n; i++)
        scanf("%d",&A[i]);

    print_subset(n,B,0);
    system("Pause");
    
    return 0;    
}

void print_subset(int n, int* B, int cur)
{
    int i;
    for(i= 0; i < cur; i++)    printf("%d ",A[B[i]]);
    printf("n");
    int s = cur ? B[cur-1]+1 : 0;//确定当前元素的最小可能位置 
    for(i = s; i < n; i++)
    {
        B[cur] = i;
        print_subset(n, B, cur+1);//递归构造子集 
    }
}

　　增量构造法可以很容易构造出指定大小的子集，只需要控制cur的大小指定输出即可，比如要输出长度不超过的3的子集，只要在程序一开始加上 if(cur>3) return; ，要输出长度为3的，只需要在for循环外加一个if就行了。

练习题：

　　1、http://www.cnblogs.com/codershell/p/3619928.html

二、含有重复元素的集合

　　如果原数组中存在重复的元素，那么用上述方法在子集生成时就会产生重复的子集，这里我是采用最简单的查重方法。代码如下：

bool isExist(vector<vector<int> > &vv,vector<int> v){
        for(int i=0; i<vv.size(); i++)
            if(vv[i] == v)
                return true;
                
        return false;
}

　　不知道有没有什么巧妙的方法来解决这个问题。

练习题：

　　http://www.cnblogs.com/codershell/p/3621687.html