目录

一、学习背景

二、简绍

三、线性表

一、什么是线性表

二、操作

1、插入

2、删除

3、查询

三、数组应用案例中源码分析

1、插入

2、删除

3、get与set

4、扩容

二、单向链表

单向链表结构

循环链表

三、数组和链表比较

1、时间复杂度角度

2、其他维度

3、灵活性/大小

重点总结

四、双向链表

1、插入

2、删除

3、查询

五、总结数据结构应用场景

数组

集合

List

Set

Map

分类总结

时间复杂度

  List

  Set

  Map

总结

---

一、学习背景

通过我们面试，算法学习，以及开发出高性能代码。

二、简绍

数据结构是计算机中存储和组织数据的一种特定方式, 常用的数据结构有数组, 字符串, 链表, 栈, 队列, 树和图等。

根据元素的组织方式, 可以分为两种， 线性结构 非线性结构。

三、线性表

一、什么是线性表

线性表就是数据排成一条线一样的结构。

比如：

数组、栈、队列、链表等等

那么有线性，就有非线性，比如：

树（二叉树）、图、堆等等

那么他们的时间复杂度到底是多少呢？

二、操作

以数组为例：int[] arr=new int[10];

数组常规操作有：插入、删除、查询

那么这些操作你会怎么做？比如：

1、插入

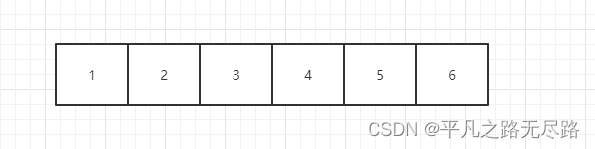
假入我们插入一个数，从下面接种场景去看

他们的时间复杂度是什么样的呢？

1、插入第一个位置

我们如果在第一个位置进行插入，这样每次都要把当前往后移动，有多少个元素移多少次，

如图：

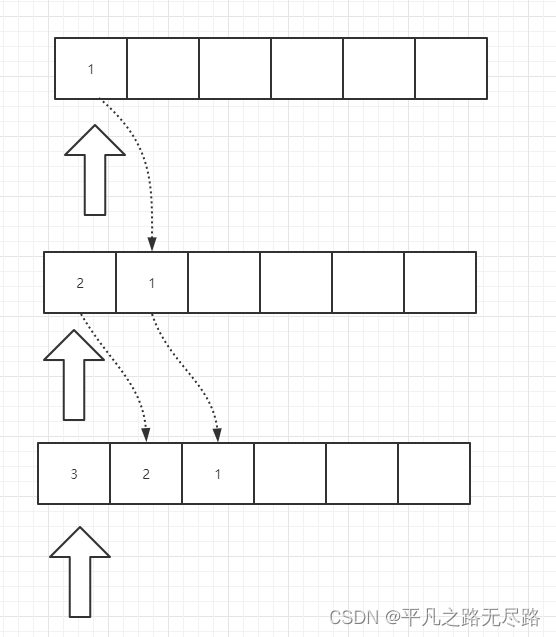
这样他的平均移动次数就是：

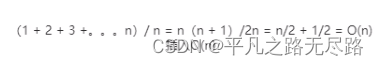
2、插入中间

我们发现插入中间和第一个位置，效果都差不多，都需要移动后面的元素，所以移动的平均值还是O(n),所以时间复杂度是O(n)。

3、插入末尾

我们指插入末尾，所以他的时间复杂度是O(1)。

2、删除

时间复杂度是什么样的？

1、删除第一个元素

这个跟插入的原理是不是一样，我每次删除第一个，元素都要往前移动一位。所以他的时间复杂度是一样的，都是O(n).

2、删除中间的元素

与插入原理一样O(n)

3、删除最后一个元素

与插入原理一样O(1)

3、查询

时间复杂度是什么样的？

查询有两种：一种根据下标查，一种根据数据查

1、根据下标查

我们直接去数组下标的某个指针下的值，他的时间复杂度是不是就是O(1).

2、根据数据查

比如我们要去找一个等于6的数。我们最好的情况就是第一次就找到了，但最坏的就是遍历一个一个查找。

所以平均来看他的算法跟上面是一样的，都是O(n)。

知识点：数组为什么是从0开始？

1、0编号的写法他可以节省编译的时间

2、Python的作者，他认为在现在语言中，0可以更优雅的表示数组字符串，

3、在支持指针的语言中，标示为偏移量，更符合逻辑

三、数组应用案例中源码分析

比如ArrayList

可以看他的插入，删除。查询对应实现，可验证时间复杂度。

1、插入

首先是扩容。后面可以看到indx都是偏移一位，每一次都是复制当前为后一个位置的值。

public void add(int index, E element) {
    rangeCheckForAdd(index);


    ensureCapacityInternal(size + 1);  // Increments modCount!!
    System.arraycopy(elementData, index, elementData, index + 1,
                     size - index);
    elementData[index] = element;
    size++;
}

显然，插入一个元素，牵连后面所有元素，这样效率就低了。

2、删除

同样可以看到他把inde元素向前移动一位。

private void fastRemove(int index) {
    modCount++;
    int numMoved = size - index - 1;
    if (numMoved > 0)
        System.arraycopy(elementData, index+1, elementData, index,
                         numMoved);
    elementData[--size] = null; // clear to let GC do its work
}

3、get与set

//get
public E get(int index) {
    rangeCheck(index);


    return elementData(index);
}
//set
public E set(int index, E element) {
    rangeCheck(index);


    E oldValue = elementData(index);
    elementData[index] = element;
    return oldValue;
}

都是根据索引进行操作的，所以他的时间复杂度是O(1).

由此可见数组的时间复杂度，就是看他有没有循环，循环几次。没有循环就是O(1)

4、扩容

我们知道所谓的扩容就是创建一个长度更大的数组。旧的的数组的元素全部复制到新的数组里面。所以显然他的效率也是比较低的。

private static final Object[] DEFAULTCAPACITY_EMPTY_ELEMENTDATA = {};


public ArrayList() {
    this.elementData = DEFAULTCAPACITY_EMPTY_ELEMENTDATA;
}

我们可以看到，我们不指定大小他会指定一个空的数组，然后在初始化为一个默认为10大小的数组。

可能我们并不需要这个大的数组，可能就是3，所以我们为何不一开始就指定他的容量呢。这样容量就省了。

所以我们一般要对ArraryList进行指定大小，这样我们就避免他扩容，以及可以只使用指定大小的容量而不浪费资源。

所以对应ArrayList初始化需要注意：

1、能不使用就不要使用默认构造函数

2、当你知道你的类表容量的时候，最好用指定的容量来创建实例。

3、如果不知道容量，预估一下，指定稍大与预估值的容量

默认容量为10.

目的：能够保证我们写出更好性能的代码。（附带面试）

二、单向链表

一、定义：

链表是一种物理存储单元上非连续，非顺序的存储结构，数据元素的逻辑顺序是通过链表中的指针链接次序实现的。

首先我们知道数据声明，他是需要一块连续的内存空间的，而链表他不需要一块连续的内存空间，它是由零散的内存创建起来的。

所以链表他是通过指针把零散的内存串联在一起，其中每一块内存就叫做链表的节点。

单向链表结构

所以从单向链表来看，每一个节点是有这些内容组成的，

有这个链表可看，它是由一个头结点和尾结点的，有了头结点我们就可以去遍历，我们可以不断的next遍历，就能找到。

而尾结点的下个节点，他其实指向的是一个null。所以当我们查询下个指向为null，则说明没有节点了。

同样我们的链表也支持，插入，删除，和查询

1、插入

我们插入是不是把上个节点指针是向需要插入的节点，插入的指向上个指针的指向节点

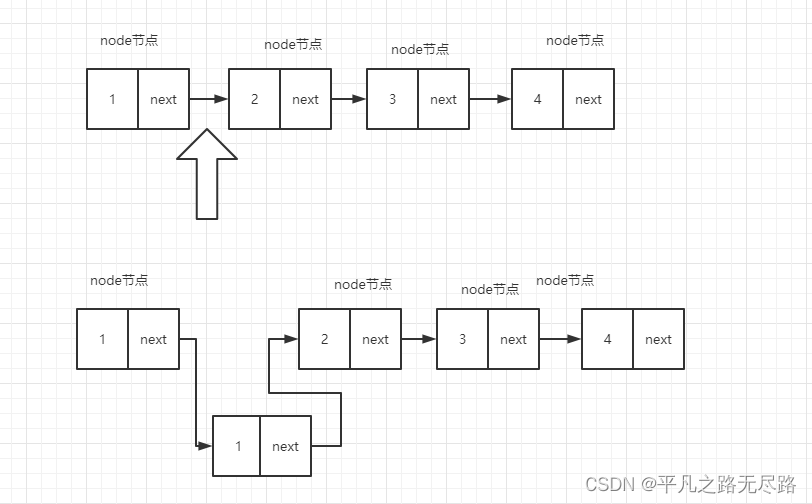
那么他的时间复杂度是不是O(1)。看上去是不是很美好，但是呢，有利就有弊。我们想一下，数组的随机访问，是不是可以指定下标，访问指定的元素。而链表可以吗？

我们即使是说，我们要第三个元素，或者第四个元素，我们是不是都要从链表的头进行取遍历。

一个个的遍历知道我们想找到的节点。

所以还是之前的逻辑 他的时间复杂度是不是就是O(n)了。

总结:插入是O(1),查询O(N).但是插入伴随着查询。

循环链表

他是一种特殊的单链表，特殊之处就是他的尾结点不在指向为一个null了。而是指向了头结点。

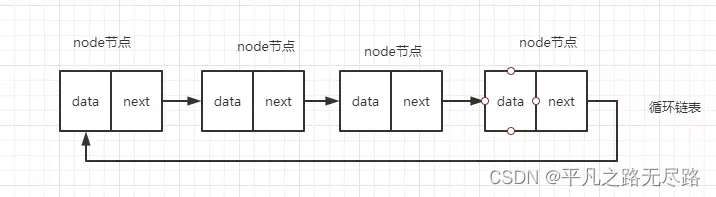
他的优点就是尾到头比较方便。

比较著名的场景就是约瑟夫环， 就是指定环中某个节点，每次遍历到他就把他从队列中剔除的一个场景。比如：排除数据，时间轮等等

三、数组和链表比较

那么什么时候使用哪一种比较好呢？

答案就是看使用场景。

1、时间复杂度角度

插入：数组O（n）、链表O(1)

随机访问：数组O(1)、链表O(n)

由此可分析出以他们为基础实现的存储结构的性能，以及使用场景。

2、其他维度

时间复杂度只是一个维度，实际中还需要看其他方面

可以看他的易用，内存连续性。

比如数组他的内存就是连续的。所以可以借助cpu的缓存机制，来预读数据，来提高数据的访问效率，所以访问速度比较快。所以他们的缺点既是优点。

3、灵活性/大小

还有就是数组的内存是固定的，你申请多少就是多少，当不够用了，你是不是要在创建一个更大的数组，然后把数据复制过去，这样是不是很耗费时间。

而链表他是没有大小限制的，他是可以动态的扩容的。就是我指针动态往后加呗，所哟他是非常灵活的。

重点总结

链表使用小建议：

1. 时刻要记住next指向的位置，指针你弄丢了他的指向，就不知道下一个是谁。
2. 有必要的取设置一个：哨兵节点，也叫dummy节点。什么场景呢？就是我们在做删除操作的时候，你能保证删除的不是这个头节点吗？如果是这个头你怎么保证返回下一个头。所以你加一个哨兵节点，你也就能保证他的一个头。
3. 写完最好进行test,对场景测试，是不是没问题。
4. 画图，进行理解
5. 多练习

四、双向链表

定义：

双向链表：是在单链表的每一个节点中，在设置一个指向其前驱节点的指针。

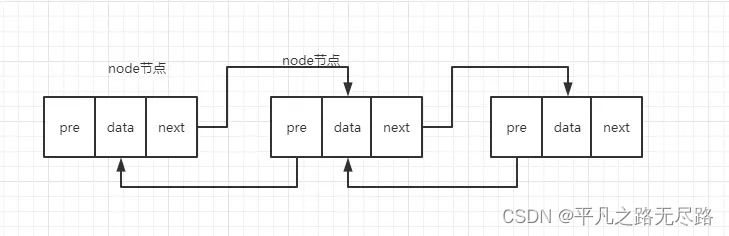
由图看，他是不是比单向链多占用一个空间。多了一个pre节点。

既然这样，她有什好处呢？

从结构上看，我们是不是可以通过O(1)的时间操作节点来找到他的前驱节点？显然不可以，

首先，还是从操作来分析：

1、插入

1. 插入指定节点前驱节点，我们是不是也要遍历一遍进行查找，然后找该节点，前驱进行插入，是不是也是O(1)。
2. 单向插入是不是要遍历查找该节点前驱，而双向则不需要遍历。直接找到了。所以时间复杂度还是O(n)和O(1)的关系。

2、删除

1. 删除某个给定的值，这个跟单向是没有区别的，不管怎么样，你都要从头遍历吧。然后在删除，所以尽管链表他的删除节点是O(1).但他掺杂了查找的操作，所以是O(n)。
2. 单向链表他要删除某一个节点的时候，是不是要找到他的前驱，因为是单向，要找到他的前驱是不是只能遍历取找。直到找到这个前驱是不是。而双向链表则不然，可以直接获取前驱结点

3、查询

1. 同样，查询的时候，同样是双向链表效率高一点。你可以记录上次查找的位置。每次要查询的时候，可以根据要找的值跟当前的值作比较，然后决定向前还是向后。所以就是虽然双向比较耗内存，但是还是比较受欢迎的地方。

就像java中LinkHashMap容器，他就是双向链表的结构。所以这个就是空间换时间概念。

所以针对执行较慢的程序，可以通过消耗更多的内存来优化，就是所谓的空间换时间，反之亦然。

五、总结数据结构应用场景

数组

与集合简单区别

• 数组固定
• 集合可变

集合

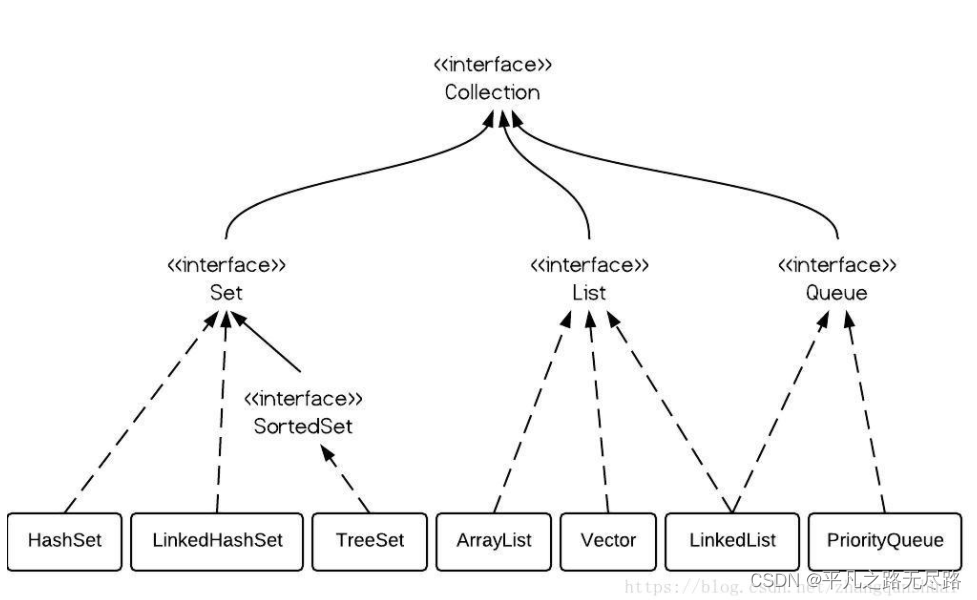
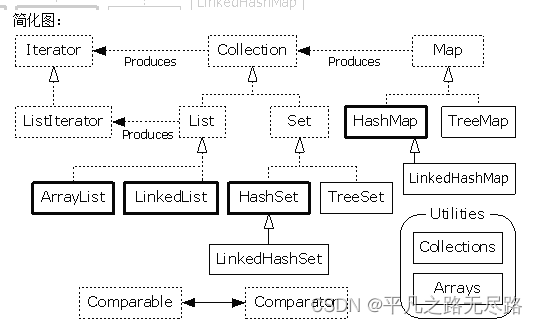
（网络图片）

List

List 有序,可重复

• ArrayList
  优点: 底层数据结构是数组，查询快，增删慢。
  缺点: 线程不安全，效率高

应用场景：是一个数组队列，相当于动态数组。它由数组实现，随机访问效率高，随机插入、随机删除效率低。

• Vector矢量队列

结构跟arrayList差不多，因效率慢，被arrayList替代
优点: 底层数据结构是数组，查询快，增删慢。
缺点: 线程安全，效率低

应用场景：是矢量队列，和ArrayList一样，它也是一个动态数组，由数组实现。但是ArrayList是非线程安全的，而Vector是线程安全的。（过时）

• LinkedList
  优点: 底层数据结构是链表，查询慢，增删快。
  缺点: 线程不安全，效率高

应用场景：是一个双向链表。它也可以被当作堆栈、队列或双端队列进行操作，随机访问效率低，但随机插入、随机删除效率低。

Set

无序,唯一

• HashSet
  底层数据结构是哈希表。(无序,唯一)
  如何来保证元素唯一性?
  1.依赖两个方法：hashCode()和equals()
• LinkedHashSet
  底层数据结构是链表和哈希表。(FIFO插入有序,唯一)
  1.由链表保证元素有序
  2.由哈希表保证元素唯一
• TreeSet
  底层数据结构是红黑树。(唯一，有序)
  1. 如何保证元素排序的呢?
  自然排序
  比较器排序
  2.如何保证元素唯一性的呢?
  根据比较的返回值是否是0来决定

应用场景：

这个如何根据场景去选择使用哪一种集合是让人头疼的问题. 简而言之,如何你需要的是一个快速的集合，建议你使用HashSet，如果你需要的是一个排序集合，请选择TreeSet，如果你需要一套能够存储插入顺序的集合,请使用LinkedHashSet。

性能对比：

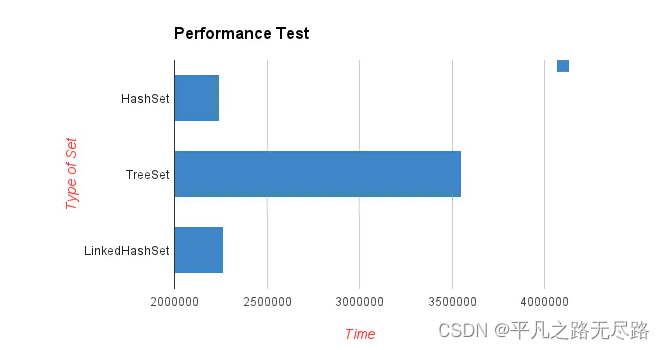
Map

• Hashtable 

接口实现类， 同步， 线程安全 是有序的

应用场景： hashTable是线程安全的一个map实现类，它实现线程安全的方法是在各个方法上添加了synchronized关键字。但是现在已经不再推荐使用HashTable了，因为现在有了ConcurrentHashMap这个专门用于多线程场景下的map实现类，其大大优化了多线程下的性能。

• HashMap 

接口实现类 ，没有同步， 线程不安全- 是无序的

 -----LinkedHashMap 双向链表和哈希表实现

应用场景：可以保存kv形式的数据，key不可重复且无序，但是查找的效率很高

• TreeMap 

红黑树对所有的key进行排序 是无序的（严格意义：TreeMap所谓的有序并不是按照数字顺序，而是字典顺序。数量key排序后看似有序，字符串排序后，就看似无序）

应用场景：TreeMap 实现了 SortMap 接口，其能够根据键排序，默认是按键的升序排序，也可以指定排序的比较器，当用 Iterator 遍历 TreeMap 时得到的记录是排过序的，所以在插入和删除操作上会有些性能损耗，TreeMap 的键不能为空，其为非并发安全 Map，此外 TreeMap 基于红黑树实现。

注意：Vector与Hashtable是旧的，是java一诞生就提供了的。

分类总结

Collection 接口的接口 对象的集合（单列集合）

├——-List 接口：元素按进入先后有序保存，可重复

│—————-├ LinkedList 接口实现类， 链表， 插入删除， 没有同步， 线程不安全

│—————-├ ArrayList 接口实现类， 数组， 随机访问， 没有同步， 线程不安全

│—————-└ Vector 接口实现类 数组， 同步， 线程安全

│ ———————-└ Stack 是Vector类的实现类

└——-Set 接口： 仅接收一次，不可重复，并做内部排序

├—————-└HashSet 使用hash表（数组）存储元素

│————————└ LinkedHashSet 链表维护元素的插入次序

└ —————-TreeSet 底层实现为二叉树，元素排好序

Map 接口 键值对的集合 （双列集合）

├———Hashtable 接口实现类， 同步， 线程安全

├———HashMap 接口实现类 ，没有同步， 线程不安全-

│—————–├ LinkedHashMap 双向链表和哈希表实现

│—————–└ WeakHashMap

├ ——–TreeMap 红黑树对所有的key进行排序

└———IdentifyHashMap

时间复杂度

  List

ArrayList

ArrayList 是线性表（数组）

get() 直接读取第几个下标，复杂度 O(1)

add(E) 添加元素，直接在后面添加，复杂度O（1）

add(index, E) 添加元素，在第几个元素后面插入，后面的元素需要向后移动，复杂度O（n）

remove（）删除元素，后面的元素需要逐个移动，复杂度O（n）

LinkedList

LinkedList 是链表的操作

get() 获取第几个元素，依次遍历，复杂度O(n)

add(E) 添加到末尾，复杂度O(1)

add(index, E) 添加第几个元素后，需要先查找到第几个元素，直接指针指向操作，复杂度O(n)

remove（）删除元素，直接指针指向操作，复杂度O(1)

Vector矢量队列

结构与ArraryList差不多

随机访问：O(1)

插入 ：  O（n）

  Set

Hashtable 

hashSet,hashtable,hashMap 都是基于散列函数， 时间复杂度 O(1) 但是如果太差的话是O(n)

HashSet

HashSet是基于散列表实现的，元素没有顺序；add、remove、contains方法的时间复杂度为O(1)。(contains为false时，就直接往集合里存)

总结：查 0（1） 增 0（1） 删0（1）

add() 复杂度为 O(1)

remove() 复杂度为 O(1)

contains() 复杂度为 O(1)

TreeSet（基于红黑树）

TreeSet是基于树实现的（红黑树），元素是有序的；add、remove、contains方法的时间复杂度为O(log (n))(contains为false时，插入前需要重新排序)。

总结：查 0（log n） 增 0（log n） 删0（log n）

add() 复杂度为 O(log (n))

remove() 复杂度为 O(log (n))

contains() 复杂度为 O(log (n))

  Map

TreeMap（基于红黑树）

平均时间复杂度 O(log n)

TreeMap基于红黑树（一种自平衡二叉查找树）实现的，时间复杂度平均能达到O(log n)。

HashMap

正常时间复杂度 O(1)~O(n)

红黑树后 O(log n)

HashMap是基于散列表实现的，时间复杂度平均能达到O(1)。正常是0(1)到0（n） jdk1.8添加了 红黑树 是 0（log n）

TreeMap的get操作的时间复杂度是O(log(n))的，相比于HashMap的O(1)还是差不少的。

LinkedHashMap

能以时间复杂度 O(1) 查找元素，又能够保证key的有序性

LinkedHashMap的出现就是为了平衡这些因素，能以O(1)时间复杂度查找元素，又能够保证key的有序性

总结

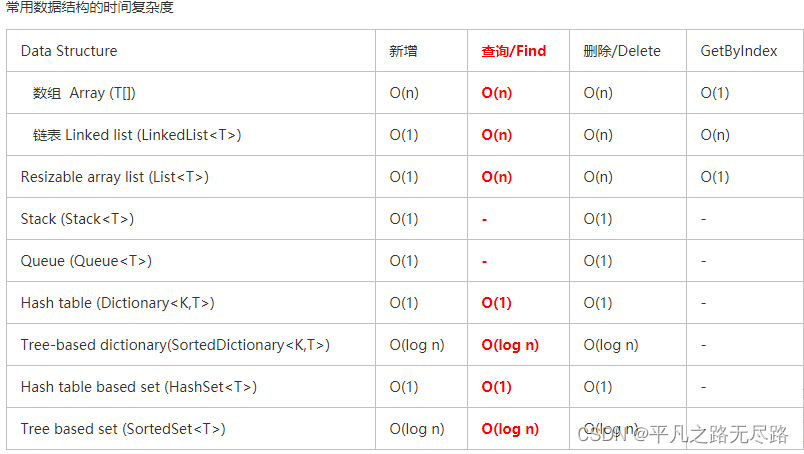
结构

Array (T[])

• 当元素的数量是固定的，并且需要使用下标时。

Linked list (LinkedList<T>)

• 当元素需要能够在列表的两端添加时。否则使用 List<T>。

Resizable array list (List<T>)

• 当元素的数量不是固定的，并且需要使用下标时。

Stack (Stack<T>)

• 当需要实现 LIFO（Last In First Out）时。

Queue (Queue<T>)

• 当需要实现 FIFO（First In First Out）时。

Hash table (Dictionary<K,T>)

• 当需要使用键值对（Key-Value）来快速添加和查找，并且元素没有特定的顺序时。

Tree-based dictionary (SortedDictionary<K,T>)

• 当需要使用价值对（Key-Value）来快速添加和查找，并且元素根据 Key 来排序时。

Hash table based set (HashSet<T>)

• 当需要保存一组唯一的值，并且元素没有特定顺序时。

Tree based set (SortedSet<T>)

• 当需要保存一组唯一的值，并且元素需要排序时。

数据结构-复杂度（一）

最后

以上就是想人陪饼干为你收集整理的数据结构-线性表与链性表（二）一、学习背景二、简绍三、线性表三、数组应用案例中源码分析二、单向链表三、数组和链表比较四、双向链表五、总结数据结构应用场景的全部内容，希望文章能够帮你解决数据结构-线性表与链性表（二）一、学习背景二、简绍三、线性表三、数组应用案例中源码分析二、单向链表三、数组和链表比较四、双向链表五、总结数据结构应用场景所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。