hdu 4629 计算几何 扫描线 (2013多校联合)

题意：给你n个三角形,可能三点共线，问覆盖1~n次的面积各是多少，n < 50

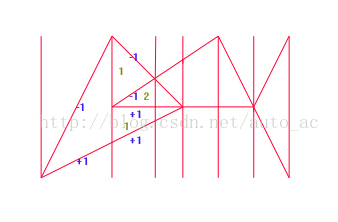
思路： 把所有线段的端点和所有的交点都放到一个数组中，并从小到大排序，然后对于每个x都画一条从下往上的垂直线，

我们枚举每两个相邻的x，单独计算它们之间的面积，这里我们从下往上扫过去。

那么我们如何知道哪块面积计算了几次呢，我们用一个 ”度“ 来表示这块面积被覆盖了几次。

以图中第二条和第三条竖线之间的面积为例， 最下面的一块一定是计算0次的，度为0， 那么当它从下往上经过第一条边时，度加1，那么上面一块的梯形就是覆盖一次，再网上穿过一条线段，度再加1，所以这块三角形的被覆盖了两次，接下来都是类似的情况， 知道扫完所有两条竖线之间的线段为止。

如何处理度呢？我们把度的信息放在线段上， 对于输入的三角形 ABC， 如何我们要取线段AB， 那么如果C在AB上方让这条线段的度为1，在下方就是-1(可以用叉积)，当然要排除AB与x轴垂直的情况。

代码注释的很详细：

#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <vector>
using namespace std;
const double eps = 1e-8;
#define pb push_back
inline int dcmp(double x) {
    if (fabs(x) < eps)
        return 0;
    return x > eps ? 1 : -1;
}
struct point {
    double x, y;
    point() {
    }
    point(const double &x, const double &y) :
            x(x), y(y) {
    }
    inline void in() {
        scanf("%lf%lf", &x, &y);
    }
    bool operator <(const point &t) const {
        return x + eps < t.x || (fabs(x - t.x) < eps && y + eps < t.y);
    }
    bool operator ==(const point &t) const {
        return !dcmp(x - t.x) && !dcmp(y - t.y);
    }
};
struct Line {
    point a, b;
    int tp;
    Line(const point &a, const point &b, const int &tp) :
            a(a), b(b), tp(tp) {
    }
    Line() {
    }
    bool operator <(const Line &t) const {
        return a < t.a || (a == t.a && b < t.b);
    }
};
double cross(const point &o, const point &a, const point &b) {
    return (a.x - o.x) * (b.y - o.y) - (a.y - o.y) * (b.x - o.x);
}
bool segSegIntersect(const point &a, const point &b, const point &l, const point &r) { // 判两线段是否相交
    if (cross(a, b, l) * cross(a, b, r) < eps
            && cross(l, r, a) * cross(l, r, b) < eps)
        return 1; // 规范相交
    return 0;
}
//********两直线求交点， 先必须判是否相交(注意排除共线)
point intersect(const point &a, const point &b, const point &l, const point &r) {
    point ret = a;
    double t = ((a.x - l.x) * (l.y - r.y) - (a.y - l.y) * (l.x - r.x))
            / ((a.x - b.x) * (l.y - r.y) - (a.y - b.y) * (l.x - r.x));
    ret.x += (b.x - a.x) * t;
    ret.y += (b.y - a.y) * t;
    return ret;
}
int n;

Line line[22504], res[22504]; //line记录所有三角形的线段，   res记录夹在相邻两个x竖线之间的线段
double X[22504];			//记录所有端点和交点的X
int c1, c2, c3;				//   line的个数，     res的个数    X的个数

double ans[55];

int main() {
    int i, j, k, cas;
    scanf("%d", &cas);
    while (cas--) {
        c1 = c2 = c3 = 0;
        scanf("%d", &n);
        for (i = 0; i < n; i++) {
            point a, b, c, tp[5];
            for (j = 0; j < 3; j++) {
                tp[j].in();
                X[c3++] = tp[j].x;
            }
            if (!dcmp(cross(tp[0], tp[1], tp[2])))		//三点共线特判掉，不特判也没关系的
                continue;
            for (j = 0; j < 3; j++)					//两两枚举三角形的边
                for (k = j + 1; k < 3; k++) {
                    a = tp[j];
                    b = tp[k];
                    if (a.x == b.x)					//排除与x轴垂直的线段
                        continue;
                    if (b < a)
                        swap(a, b);
                    c = tp[3 - j - k];
                    line[c1++] = Line(a, b, dcmp(cross(a, b, c)));    //叉积判上下方非常方便
                }
        }
		//得到所有线段的交点
        for (i = 0; i < c1; i++)	
            for (j = i + 1; j < c1; j++) {
                if (!segSegIntersect(line[i].a, line[i].b, line[j].a,
                        line[j].b))
                    continue;
                point tp = intersect(line[i].a, line[i].b, line[j].a,
                        line[j].b);
                X[c3++] = tp.x;
            }
        sort(X, X + c3);		//X排序去重
		c3 = unique(X, X+c3)-X;
        for (i = 0; i <= n; i++)
            ans[i] = 0.0;
        for (i = 1; i < c3; i++) {    //枚举相邻的X  即  X[i-1] 与X[i]
            c2 = 0;
            for (j = 0; j < c1; j++)		//枚举所有三角形的边
                if (line[j].a.x <= X[i - 1] && X[i] <= line[j].b.x) {			//线段在该区域里面，确保有交点
                    point a = intersect(line[j].a, line[j].b, point(X[i-1], 0),
                            point(X[i-1], 1));
                    point b = intersect(line[j].a, line[j].b, point(X[i], 0),
                            point(X[i], 1));
                    res[c2++] = Line(a, b, line[j].tp);		//把夹在 X[i-1] 与X[i]这两条竖线之间的线段保存下来
                }
            sort(res, res + c2);			
            if (c2) {
                int deep = res[0].tp;
                for (j = 1; j < c2; j++) { //从下往上遍历所有线段并计算面积
                    double h = res[j].b.x - res[j].a.x;
                    double b = fabs(res[j - 1].a.y - res[j].a.y)
                            + fabs(res[j - 1].b.y - res[j].b.y);
                    if (deep)
                        ans[deep] += b * h / 2;	
                    deep += res[j].tp;		//修改度
                }
            }
        }

        for (i = 1; i <= n; i++)
            printf("%.10fn", ans[i]);
    }
    return 0;
}

最后

以上就是敏感冬瓜为你收集整理的hdu 4629 计算几何 扫描线 (2013多校联合)的全部内容，希望文章能够帮你解决hdu 4629 计算几何 扫描线 (2013多校联合)所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。