题目大意:在整个范围内给出若干个矩形,在给出一个数字d,要让我们找到一个坐标(x,y),使得(x+0.5+kd,y+0.5+kd)(k取任意值)不会落入任何一个矩形里.如果有就输出任意一个坐标,没有就输出no
本题的关键点是(x+0.5+kd,y+0.5+kd),如果我们把整张图分成许多d*d的小正方形,就会出现如图的情况
(本图来源于题解的ppt)
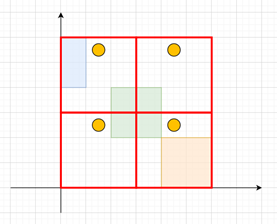
其中的黄色圆点就是我们想要找的点,我们可以看到如果我们将每个dd小块中被矩形占据的位置"移动"到左下角的小块中,就会出现如图的情况
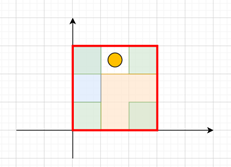
也就是说我们只需要在dd的小正方形中要到一个这样的"空隙"那么这个地方就是答案
根据这个图的特征,我们很容易想到用线段树+扫描线来解决.
(本图来源于acwing)
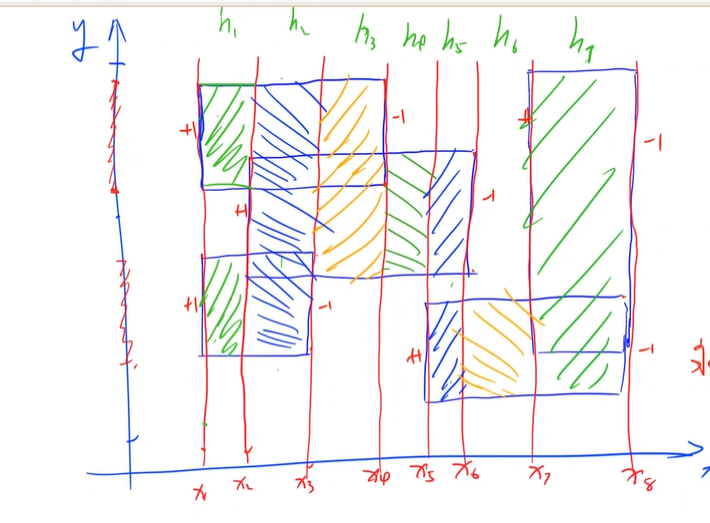
对于其中一个矩形而言,我们平行x轴做一条穿过该矩形的线,线接触到矩形的第一个的边赋值为1,第二个接触矩形第二个边赋值为-1
我们先记录图中好x1,x2,x3……xn的位置,对于每个分块里矩形的边,我们又以L,R记录好其在Y轴上的坐标
以一个邻接表来储存这些信息
struct node2 {
int l, r, x;
};
vector<node2>vt[N];
vt[i]的表示横坐标在i上的所有边,x代表这个边是1还是-1(开始边,结束边) L,R代表其在Y轴上的坐标
以y轴做一个线段树,树的每个节点维护两个值
struct node1 {
int cnt;//当前区间整个被覆盖多少次(对应图中的1,-1)
int len;//当前区间cnt>0的区间总长和
} tr[N * 4];
随后按从左到右的顺序逐步加入边,直到某一次加入后tr[1]的len要<d,这就说明在当前[Xn,Xn+1]区间中必定有一个"空隙",由此确定答案的X轴坐标,然后就用线段树找出其Y坐标
以下是完整代码
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
int n, d, ql, qr, x;
struct node1 {
int cnt;//当前区间整个被覆盖多少次(对应图中的1,-1)
int len;//当前区间cnt>0的区间总长和
} tr[N * 4];
struct node2 {
int l, r, x;//扫描线,x=1是开始边,x=-1是结束边
};
vector<node2>vt[N];//记录扫描线
void mod(int &x) {//取模
x %= d;
while (x < 0)
x += d;
}
void add(int x1, int x2, int y1, int y2) {
vt[x1].push_back({y1, y2, 1});//覆盖开始
vt[x2 + 1].push_back({y1, y2, -1});//覆盖结束
}
void pushup(int u, int l, int r) {
if (tr[u].cnt)
tr[u].len = r - l + 1;
else if (l == r)
tr[u].len = 0;
else
tr[u].len = tr[u << 1].len + tr[u << 1 | 1].len;
}
void change(int u, int l, int r) {
if (ql <= l && r <= qr) {//完全覆盖在一个开始/结束边中
tr[u].cnt += x;//cnt 覆盖次数
pushup(u, l, r);
return;
}
int mid = l + r >> 1;
if (ql <= mid)
change(u << 1, l, mid);
if (mid < qr)
change(u << 1 | 1, mid + 1, r);
pushup(u, l, r);
}
void get(int u, int l, int r) {
if (tr[u].len == 0) {//当前节点没有覆盖面积
cout << l << endl;
return ;
}
int mid = l + r >> 1;
if (tr[u << 1].len < mid - l + 1)//只要左半边的覆盖面积小于总面积的一半,说明左边必定有空隙
get( u << 1, l, mid);
else
get(u << 1 | 1, mid + 1, r );
}
int main() {
cin >> n >> d;
for (int i = 1; i <= n; i++) {
int x1, y1, x2, y2;
cin >> x1 >> y1 >> x2 >> y2;
x2--, y2--;
if (x2 - x1 + 1 >= d)
x1 = 0, x2 = d - 1;
if (y2 - y1 + 1 >= d)
y1 = 0, y2 = d - 1;
mod(x1), mod(x2), mod(y1), mod(y2);
if (x1 <= x2) {
if (y1 <= y2)
add(x1, x2, y1, y2);
else//y1比y2大,在投影到d*d时y2比y1小
add(x1, x2, 0, y2), add(x1, x2, y1, d - 1);
} else {
if (y1 <= y2)
add(0, x2, y1, y2), add(x1, d - 1, y1, y2);
else
add(0, x2, 0, y2), add(x1, d - 1, 0, y2), add(0, x2, y1, d - 1), add(x1, d - 1, y1, d - 1);
}
}
for (int i = 0; i < d; i++) {
int sz = vt[i].size();
for (int j = 0; j < sz; j++) {
ql = vt[i][j].l, qr = vt[i][j].r;
x = vt[i][j].x;
change(1, 0, d - 1); //源点 左边界 右边界
}
if (tr[1].len < d) {//如果在当前区块中总覆盖面积小于d,说明必定有空隙
cout << "YES" << endl << i << " ";
get(1, 0, d - 1);
return 0;
}
}
cout<<"NO"<<endl;
return 0;
}
最后
以上就是傻傻春天最近收集整理的关于2021牛客多校6H Hopping Rabbit (线段树+扫描线)的全部内容,更多相关2021牛客多校6H内容请搜索靠谱客的其他文章。








发表评论 取消回复