Snowy Smile【扫描线】【2019 杭电多校6】

65 阅读 0 评论 43 点赞

我是靠谱客的博主糊涂钢笔，最近开发中收集的这篇文章主要介绍Snowy Smile【扫描线】【2019 杭电多校6】，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

HDU-6638 题目链接

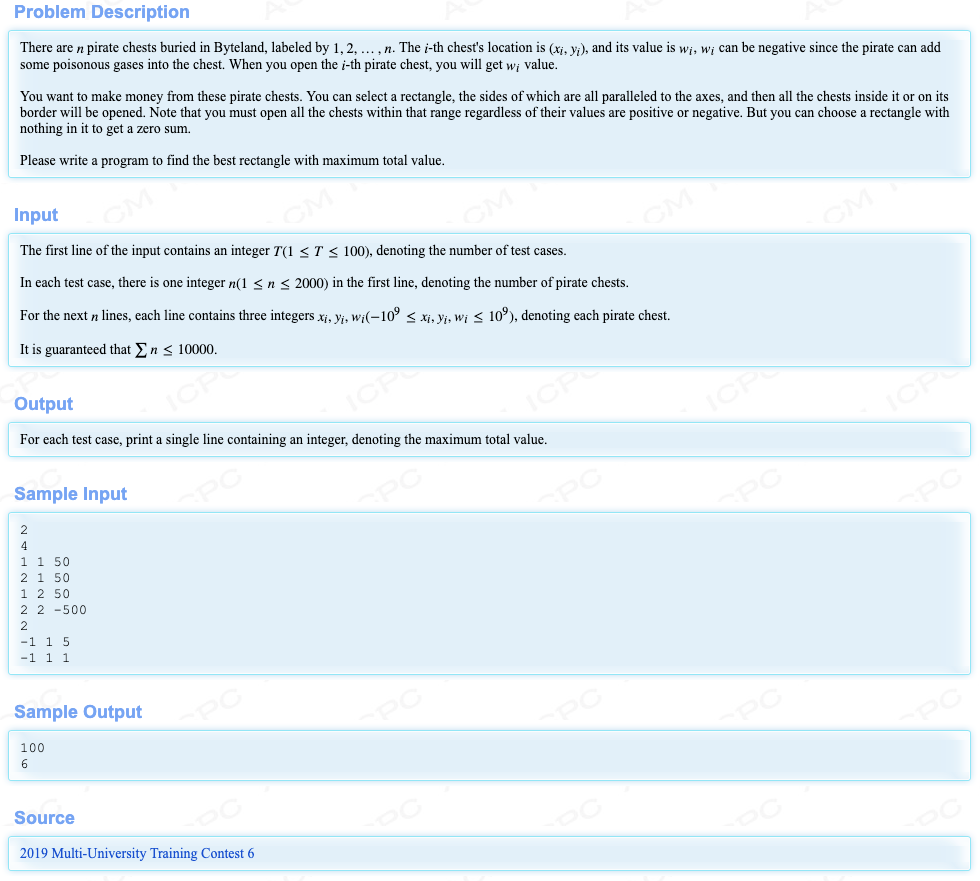
比赛的时候只在拼命的想怎么去优化O(N^3)的那个之前所认为的标准解法，没想到，这就是一道O(N^2 * logN)的扫描线。

我们可以固定上下两个区间，然后在固定的区域中，就是一维的空间了，我们直接在这一维里去查询即可，然后去寻找区间最大连续子段即可，很方便的。

区间最大连续子段：

我们要查最大左端点，最大右端点，还有整个区间段的和，以及该区间段内的最大值。

然后维护左右段最大连续，都是去比较，子区间的端点最大连续和子区间整个和加上另一个子区间的该方向最大连续。

然后区间最大值，就是去比较左右最大值，左右连续，左子区间的右连续和右子区间的左连续之和，这几个的最大值。

#include <iostream>
#include <cstdio>
#include <cmath>
#include <string>
#include <cstring>
#include <algorithm>
#include <limits>
#include <vector>
#include <stack>
#include <queue>
#include <set>
#include <map>
#define lowbit(x) ( x&(-x) )
#define pi 3.141592653589793
#define e 2.718281828459045
#define INF 0x3f3f3f3f
#define HalF (l + r)>>1
#define lsn rt<<1
#define rsn rt<<1|1
#define Lson lsn, l, mid
#define Rson rsn, mid+1, r
#define QL Lson, ql, qr
#define QR Rson, ql, qr
#define myself rt, l, r
#define MAX_3(x, y, z) max(x, max(y, z))
#define MAX_6(a, b, c, d, f, g) max(max(a, b), max(max(c, d), max(f, g)))
using namespace std;
typedef unsigned long long ull;
typedef long long ll;
const int maxN = 2007;
int N, lsan_x[maxN], lsan_y[maxN], len_x, len_y;
vector<int> vt[maxN];
struct node
{
    int x, y; ll val;
    node(int a=0, int b=0, ll c=0):x(a), y(b), val(c) {}
}a[maxN];
bool cmp(node e1, node e2) { return e1.x == e2.x ? e1.y < e2.y : e1.x < e2.x; }
struct make_Tree
{
    ll mx, lm, rm, all;
    make_Tree(ll a=0, ll b=0, ll c=0, ll d=0):mx(a), lm(b), rm(c), all(d) {}
}tree[maxN<<2];
void buildTree(int rt, int l, int r)
{
    tree[rt] = make_Tree();
    if(l == r) return;
    int mid = HalF;
    buildTree(Lson); buildTree(Rson);
}
inline void pushup(int rt)
{
    if(tree[lsn].lm > tree[lsn].all + tree[rsn].lm) tree[rt].lm = tree[lsn].lm;
    else tree[rt].lm = tree[lsn].all + tree[rsn].lm;
    
    if(tree[rsn].rm > tree[rsn].all + tree[lsn].rm) tree[rt].rm = tree[rsn].rm;
    else tree[rt].rm = tree[rsn].all + tree[lsn].rm;
    
    tree[rt].all = tree[lsn].all + tree[rsn].all;
    tree[rt].mx = MAX_6(tree[rt].lm, tree[rt].rm, tree[lsn].mx, tree[rsn].mx, tree[lsn].rm + tree[rsn].lm, tree[rt].all);
}
void update(int rt, int l, int r, int qx, ll val)
{
    if(l == r)
    {
        if(val >= 0) tree[rt] = make_Tree(val, val, val, val);
        else tree[rt] = make_Tree(0, 0, 0, val);
        return;
    }
    int mid = HalF;
    if(qx <= mid) update(Lson, qx, val);
    else update(Rson, qx, val);
    pushup(rt);
}
inline ll query(int rt, int l, int r, int ql, int qr)
{
    if(ql <= l && qr >= r) return tree[rt].mx;
    int mid = HalF;
    if(qr <= mid) return query(QL);
    else if(ql > mid) return query(QR);
    else
    {
        ll ans = tree[lsn].rm + tree[rsn].lm;
        ans = MAX_3(ans, query(QL), query(QR));
        return ans;
    }
}
int main()
{
    int Cas; scanf("%d", &Cas);
    while(Cas--)
    {
        scanf("%d", &N);
        for(int i=1; i<=N; i++) vt[i].clear();
        for(int i=1; i<=N; i++)
        {
            scanf("%d%d%lld", &a[i].x, &a[i].y, &a[i].val);
            lsan_x[i] = a[i].x; lsan_y[i] = a[i].y;
        }
        sort(lsan_x + 1, lsan_x + N + 1);
        sort(lsan_y + 1, lsan_y + N + 1);
        len_x = (int)(unique(lsan_x + 1, lsan_x + N + 1) - lsan_x - 1);
        len_y = (int)(unique(lsan_y + 1, lsan_y + N + 1) - lsan_y - 1);
        for(int i=1; i<=N; i++)
        {
            a[i].x = (int)(lower_bound(lsan_x + 1, lsan_x + len_x + 1, a[i].x) - lsan_x);
            a[i].y = (int)(lower_bound(lsan_y + 1, lsan_y + len_y + 1, a[i].y) - lsan_y);
        }
        sort(a + 1, a + N + 1, cmp);
        int tot = 0;
        for(int i=1, j=0; i<=N; )
        {
            j = i + 1;
            while(a[j].x == a[i].x && a[j].y == a[i].y)
            {
                a[i].val += a[j].val;
                j++;
            }
            a[++tot] = node(a[i].x, a[i].y, a[i].val);
            i = j;
        }
        for(int i=1; i<=tot; i++)
        {
            vt[a[i].x].push_back(i);
        }
        ll ans = 0;
        for(int i=1; i<=len_x; i++)
        {
            buildTree(1, 1, len_y);
            ll sum[maxN] = {0};
            for(int j=i; j<=len_x; j++)
            {
                int len = (int)vt[j].size();
                for(int k=0, pos; k<len; k++)
                {
                    pos = vt[j][k];
                    sum[a[pos].y] += a[pos].val;
                    update(1, 1, len_y, a[pos].y, sum[a[pos].y]);
                }
                ans = max(ans, query(1, 1, len_y, 1, len_y));
            }
        }
        printf("%lldn", ans);
    }
    return 0;
}