hdu541(树状数组）

这个名词不陌生然而到现在 我才发现我没有做过这类型的题。。一点概念都没有

                                                                                                                                                           天下烦心事之悠悠，独怆然而奋发向上

首先祭经典图

（来自http://www.cnblogs.com/zhangshu/archive/2011/08/16/2141396.html）

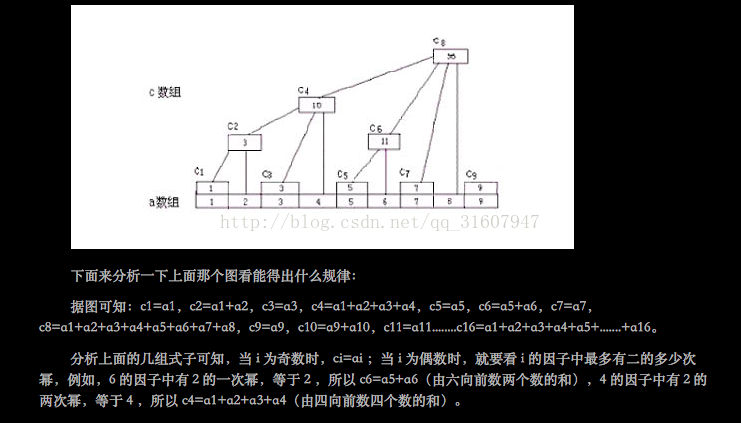
这样就把要列为树状数组的a转化为了c

int lowboy(int i)

   return i&(-i);

出来的值就是可喜可贺的i的因子中2的多少次方的个数，比如4为4，6为2，7为1之类

然后求这个数组的和（树状数组的作用就是为求和时省时）

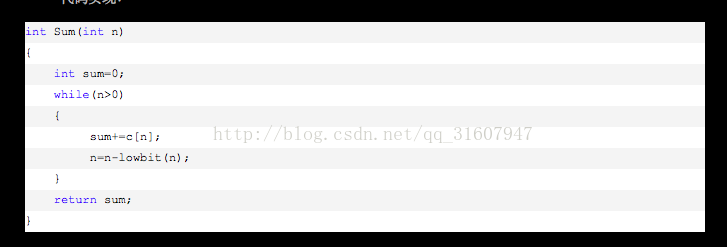
这个求和蛮巧妙，很省时

n=n-lowbit(n)就是减去了n这个值可以囊括的lowbit ，比如若是n为5，减去后n就为4了，因为c[5]只有a[5]一个值。当n为4时减去后为0，因为c[4]包含了a[1]~a[4]，然后就不用再加了

接下来是更新后再求和

把每一个包括了a[i]的c[i]跟新

题意：给n个星星，每个星星按y坐标从小到大，y一样x从小到大输入，然后每个星星的做下区域每包含一个星星（不包括自己），该星星就升一级；最后求等级0~n-1的星星的个数

a[i]表示坐标为i的点的level，

sum[i]为level为i的个数

#include <cstdio>

#include <cstring>

#include <cmath>

#include <algorithm>

using namespacestd;

#define MAXN 32010

int n,a[MAXN],sum[MAXN];

int lowbit(int x){return x&(-x);}

int Sum(int n)///前n项的和

{

    int s =0;

    while(n >0)

    {

        s += a[n];

        n -= lowbit(n);

    }

    return s;

}

void add(int x)///增加某个元素的大小

{

    while(x <=MAXN)

    {

        ++a[x];

        x += lowbit(x);

    }

}

int main()

{

    int x,y;

    while(~scanf("%d",&n))

    {

        memset(a,0,sizeof(a));

        memset(sum,0,sizeof(sum));

        for(int i=0; i<n; i++)

        {

            scanf("%d%d",&x,&y);

            x++;

            sum[Sum(x)]++;

            add(x);

        }

        for(int i=0; i<n; i++)

            printf("%dn",sum[i]);

    }

    return0;

}

最后

以上就是感性大门为你收集整理的hdu541(树状数组）的全部内容，希望文章能够帮你解决hdu541(树状数组）所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。