
相交线与平行线知识点(全)
平面内,点与直线之间的位置关系分为两种:① 点在线上 ② 点在线外
同一平面内,两条或多条不重合的直线之间的位置关系只有两种:① 相交 ② 平行
 一、相交线
一、相交线
1、两条直线相交,有且只有一个交点。(反之,若两条直线只有一个交点,则这两条直线相交。)
两条直线相交,产生邻补角和对顶角的概念:
邻补角:两角共一边,另一边互为反向延长线。邻补角互补。要注意区分互为邻补角与互为补角的异同。
对顶角:两角共顶点,一角两边分别为另一角两边的反向延长线。对顶角相等。
注:①、同角或等角的余角相等;同角或等角的补角相等;等角的对顶角相等。反过来亦成立。
②、表述邻补角、对顶角时,要注意相对性,即“互为”,要讲清谁是谁的邻补角或对顶角。例如:
判断对错:因为∠ABC +∠DBC = 180°,所以∠DBC是邻补角。
相等的两个角互为对顶角。
2、垂直是两直线相交的特殊情况。注意:两直线垂直,是互相垂直,即:若线a垂直线b,则线b垂直线a 。
垂足:两条互相垂直的直线的交点叫垂足。垂直时,一定要用直角符号表示出来。
过一点有且只有一条直线与已知直线垂直。(注:这一点可以在已知直线上,也可以在已知直线外)
3、点到直线的距离。
垂线段:过线外一点,作已知线的垂线,这点到垂足之间的线段叫垂线段。
垂线与垂线段:垂线是一条直线,而垂线段是一条线段,是垂线的一部分。
垂线段最短:连接直线外一点与直线上各点的所有线段中,垂线段最短。(或说直角三角形中,斜边大于直角边。)
点到直线的距离:直线外一点到这条直线的垂线段的长度,叫这点到直线的距离。注:距离指的是垂线段的长度,而不是这条垂线段的本身。所以,如果在判断时,若没有“长度”两字,则是错误的。
4、同位角、内错角、同旁内角
三线六面八角:平面内,两条直线被第三条直线所截,将平面分成了六个部分,形成八个角,其中有:4对同位角,2对内错角和2对同旁内角。注意:要熟练地认识并找出这三种角:① 根据三种角的概念来区分 ② 借助模型来区分,即:同位角——F型,内错角——Z型,同旁内角——U型。
特别注意:
① 三角形的三个内角均互为同旁内角;
② 同位角、内错角、同旁内角的称呼并不一定要建立在两条平行的直线被第三条直线所截的前提上才有的,这两条直线也可以不平行,也同样的有同位角、内错角、同旁内角。
5、几何计数:
① 平面内n条直线两两相交,共有n ( n – 1) 组对顶角。(或写成 n^2 – n 组)
② 平面内n条直线两两相交,最多有n(n–1)/2个交点。(或写成(n^2–n)/2个)
③ 平面内n条直线两两相交,最多把平面分割成[n(n+1)/2]+1个面。
④ 当平面内n个点中任意三点均不共线时,一共可以作n(n–1)/2 条直线。
回顾:
ⅰ、一条直线上n个点之间,一共有n(n–1)/2 条线段;
ⅱ、若从一个点引出n条射线,则一共有n(n–1)/2 个角。
 二、平行线
二、平行线
同一平面内,两条直线若没有公共点(即交点),那么这两条直线平行。注:平行线永不相交。
1、平行公理:过直线外一点,有且只有一条直线与已知直线平行。(注:这一点是在直线外)
推论:如果两条直线都与第三条直线平行,那么这两条直线也互相平行。(或叫平行线的传递性)
2、平行线的画法:借助三角板和直尺。具体略。(此基本作图方法一定要掌握,多练习。)
3、平行线的判定:
① 同位角相等,两直线平行;
② 内错角相等,两直线平行;
③ 同旁内角互补,两直线平行。
注意:是先看角如何,再判断两直线是否平行,前提是“角相等/ 互补”。
一个重要结论:同一平面内,垂直于同一直线的两条直线互相平行。
4、平行线的性质:
① 两直线平行,同位角相等;
② 两直线平行,内错角相等;
③ 两直线平行,同旁内角互补。
注意:是先有两直线平行,才有以上的性质,前提是“线平行”。
一个结论:平行线间的距离处处相等。例如:应用于 说明矩形(包括长方形、正方形)的对边相等,还有梯形的对角线把梯形分成分别以上底为底的两等面积的三角形,或 以下底为底的两等面积的三角形。(因为梯形的上底与下底平行,平行线间的高相等,所以,就有等底等高的三角形。)
※ 此章难度最大就在如何利用平行线的判定或性质来进行解析几何的初步推理,要在熟练掌握好基本知识点的基础上,学会逻辑推理,既要条理清晰,又要简洁明了。
5、命题
判断一件事情的语句叫命题。命题包括“题设”和“结论”两部分,可写成“如果……那么……”的形式。
例如:“明天可能下雨。”这句语句______命题,而“今天很热,明天可能下雨。”这句语句_____命题。(填“是”或“不是”)
① 命题分为真命题 与 假命题,真命题指题设成立,结论也成立的命题(或说正确的命题)。假命题指题设成立,但结论不一定或根本不成立的命题(或说错误的命题)。
② 逆命题:将一个命题的题设与结论互换位置之后,形成新的命题,就叫原命题的逆命题。
注:原命题是真命题,其逆命题不一定仍为真命题,同理,原命题为假命题,其逆命题也不一定为假命题。
例如:“对顶角相等”是个真命题,但其逆命题“______”却是个假命题。
不论是真命题还是假命题,都要学会能非常熟练地把一个命题写成“如果……那么……”的形式。例:把“等角的补角相等”写成“如果…… 那么……”的形式为:_________。
再例:把“三角形的内角和等于180度。”写成包含题设与结论的形式:______________________。
 三、平移
三、平移
1、 概念:把图形的整体沿着某一方向移动一定的距离,得到一个新的图形,这种图形的移动,叫平移。
确定平移,关键是要弄清平移的方向(并不一定是水平移动或垂直移动哦)与平移的距离。如果是斜着平移的,则需把由起始位置至最终位置拆分为先水平移动,再上下移动,或拆分为先上下移动,再水平移动。当然,如果是在格点图内平移,则可利用已知点的平移距离是某一矩形的对角线这一特点来对应完成其它顶点的平移。
2、 特征:
① 发生平移时,新图形与原图形的形状、大小完全相同(即:对应线段、对应角均相等);
② 对应点之间的线段互相平行(或在同一直线上)且相等,均等于平移距离。
3、画法:掌握平移方向与平移距离,利用对应点(一般指图形的顶点)之间连线段平行、连线段相等性质描出原图形顶点的对应点,再依次连接,就形成平移后的新图形。
矩形、菱形、正方形的5大考点及题型汇总
 一、矩形、菱形、正方形的性质
一、矩形、菱形、正方形的性质
1.矩形的性质
①具有平行四边形的一切性质;
②矩形的四个角都是直角;
③矩形的对角线相等;
④矩形是轴对称图形,它有两条对称轴;
⑤直角三角形斜边上的中线等于斜边的一半。
2.菱形的性质
①具有平行四边形的一切性质;
②菱形的四条边都相等;
③菱形的两条对角线互相垂直,并且每一条对角线平分一组对角;
④菱形是轴对称图形,每条对角线所在的直线都是它的对称轴;
⑤菱形的面积=底×高=对角线乘积的一半。
3.正方形的性质
正方形具有平行四边形,矩形,菱形的一切性质
①边:四边相等,对边平行;
②角:四个角都是直角;
③对角线:互相平分;相等;且垂直;每一条对角线平分一组对角,即正方形的对角线与边的夹角为45度;
④正方形是轴对称图形,有四条对称轴。
例1 矩形ABCD中,DE⊥AC于E,且∠ADE:∠EDC=3:2,则∠BDE的度数为 ( )
A.360 B.90
C.270 D.180
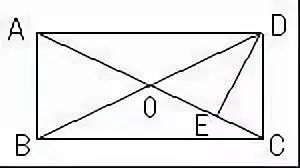
例2 如图,矩形ABCD中,AE⊥BD于点E,对角线AC与BD相交于点O,BE:ED=1:3,AB=6cm,求AC的长。
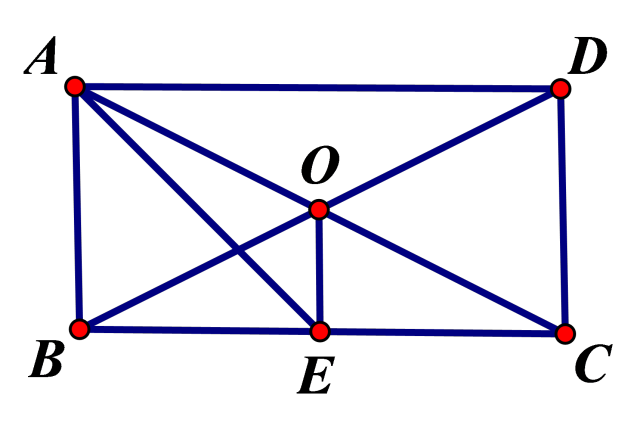
例3 如图, O是矩形ABCD 对角线的交点, AE平分 ∠BAD,∠AOD=120° ,求∠AEO 的度数。
例4 菱形的周长为40cm,两邻角的比为1:2,则较短对角线的长________ 。
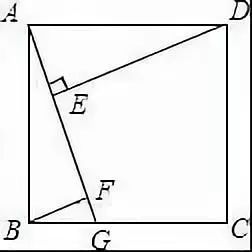
例5 如图,在正方形ABCD中,G是BC上任意一点,连接AG,DE⊥AG于E,BF∥DE交AG于F,探究线段AF、BF、EF三者之间的数量关系,并说明理由.
 二、矩形、菱形、正方形的判定
二、矩形、菱形、正方形的判定
1.矩形的判定
①有一个内角是直角的平行四边形是矩形;
②对角线相等的平行四边形是矩形;
③有三个角是直角的四边形是矩形;
④还有对角线相等且互相平分的四边形是矩形。
2.菱形的判定方法
①有一组邻边相等的平行四边形是菱形;
②对角线互相垂直的平行四边形是菱形;
③四条边都相等四边形是菱形;
④对角线垂直平分的四边形是菱形。
3.正方形的判定
①菱形+矩形的一条特征;
②菱形+矩形的一条特征;
③平行四边形+一个直角+一组邻边相等。
说明一个四边形是正方形的一般思路是:先判断它是矩形,在判断这个矩形也是菱形;或先判断它是菱形,再判断这个菱形也是矩形。
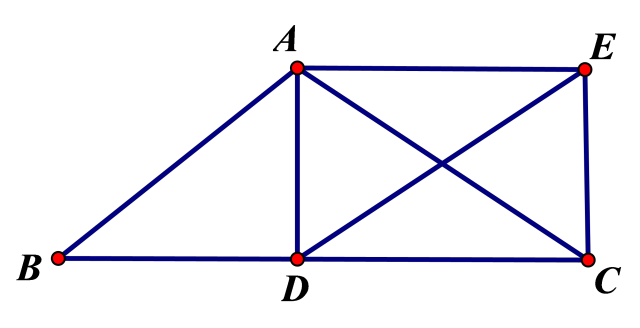
例1. 如图,在△ABC中,AB=AC,点D是边BC的中点,过点A、D分别作BC与AB的平行线,并交于点E,连续EC、AD。
求证:四边形ADCE是矩形。
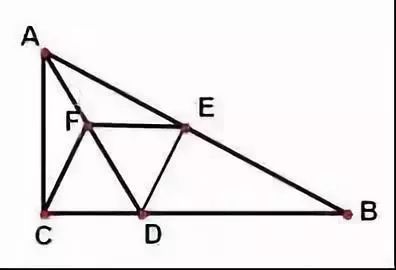
例2.如图,△ABC中,∠C=90°,AD平分∠BAC,ED⊥BC,DF//AB.
求证:AD与EF互相垂直平分。
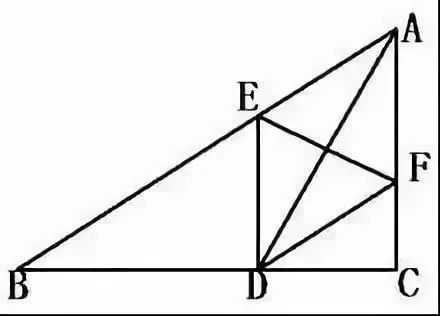
例3.已知如图,在△ABC,∠ACB=900,AD是角平分线,点E、F分别在AB、AD上,且AE=AC,EF∥BC。
求证:四边形CDEF是菱形。
 三、矩形、菱形、正方形与函数综合题
三、矩形、菱形、正方形与函数综合题
1.利用矩形、菱形、正方形的知识解决函数问题;
2.利用函数知识解决矩形、菱形、正方形的问题;
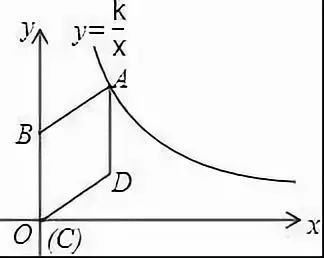
例1.如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数y=(k>0,x>0)的图象上,点D的坐标为(4,3).
(1)求k的值;
(2)若将菱形ABCD沿x轴正方向平移,当菱形的顶点D落在函数y=(k>0,x>0)的图象上时,求菱形ABCD沿x轴正方向平移的距离。
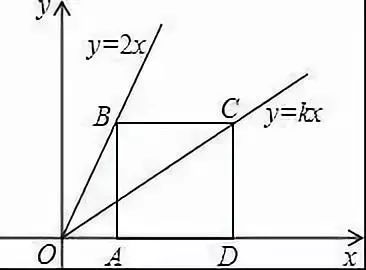
例2.如图,点B、C分别在两条直线y=2x和y=kx上,点A、D是x轴上两点,已知四边形ABCD是正方形,则k值为______.
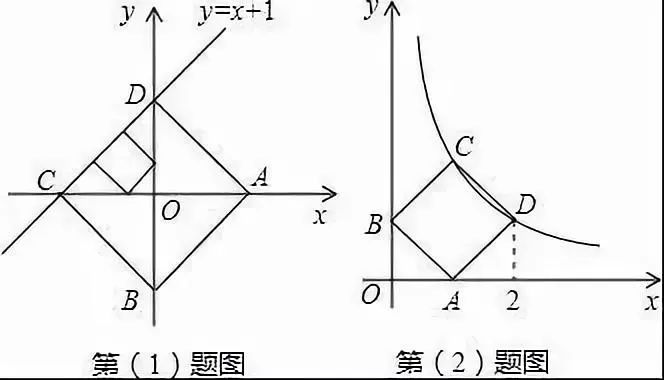
例3 已知点A、B分别是x轴、y轴上的动点,点C、D是某个函数图象上的点,当四边形ABCD(A、B、C、D各点依次排列)为正方形时,称这个正方形为此函数图象的伴侣正方形.例如:如图,正方形ABCD是一次函数y=x+1图象的其中一个伴侣正方形.
(1)若某函数是一次函数y=x+1,求它的图象的所有伴侣正方形的边长;
(2)若某函数是反比例函数,它的图象的伴侣正方形为ABCD,点D(2,m)(m<2)在反比例函数图象上,求m的值及反比例函数解析式。
 四、矩形、正方形的翻折
四、矩形、正方形的翻折
1.从翻折中找出对称轴,利用对称性找相等关系。
2.利用相等关系建立方程解决问题。
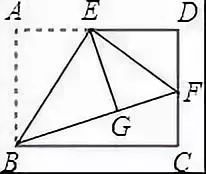
例1 如图,矩形ABCD中,E是AD的中点,将△ABE沿直线BE折叠后得到△GBE,延长BG交CD于点F.若CF=1,FD=2,则BC的长是( )
A.3√6 B.2√6
C.2√5 D.2√3
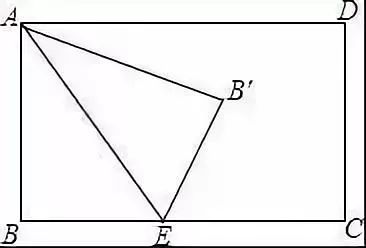
例2 如图,在矩形ABCD中,AB=5,BC=7,点E为BC上一动点,把△ABE沿AE折叠,当点B的对应点B′落在∠ADC的角平分线上时,则点B′到BC的距离为( )
A.1或2 B. 2或3
C.3或4 D. 4或5
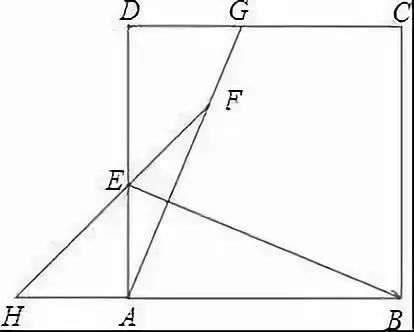
例3 如图,在边长为1的正方形ABCD中,E为AD边上一点,连接BE,将△ABE沿BE对折,A点恰好落在对角线BD上的点F处。延长AF,与CD边交于点G,延长FE,与BA的延长线交于点H,则下列说法:①△BFH为等腰直角三角形;②△ADF≌△FHA;③∠DFG=60°;④DE=2-√2;⑤S△AEF=S△DFG.其中正确的说法有( )
A.1个 B.2个
C.3个 D.4个
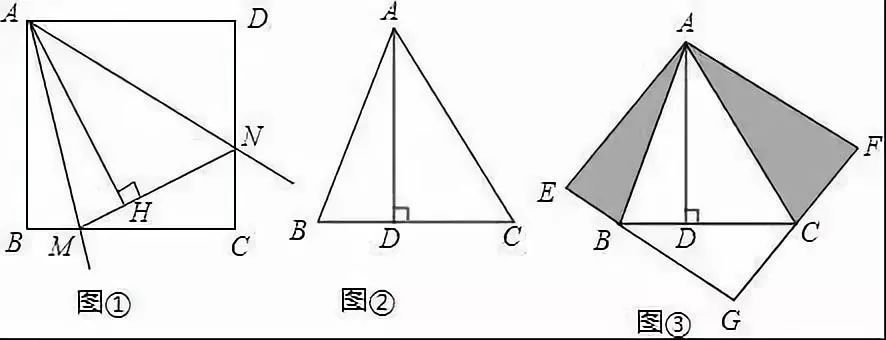
例4 四边形ABCD是正方形,∠MAN=45°,它的两边AM、AN分别交CB、DC与点M、N,连接MN,作AH⊥MN,垂足为点H。
(1)如图1,猜想AH与AB有什么数量关系?并证明。
(2)如图2,已知∠BAC=45°,AD⊥BC于点D,且BD=2,CD=3,求AD的长。
 五、综合运用
五、综合运用
1.计算。利用矩形、菱形、正方形中的等腰三角形和直角三角形进行计算。
2.证明。利用矩形、菱形、正方形的性质和判定,结合全等三角形、等腰三角形、等边三角形的知识展开证明。
3.探究。利用矩形、菱形、正方形等知识展开探究。
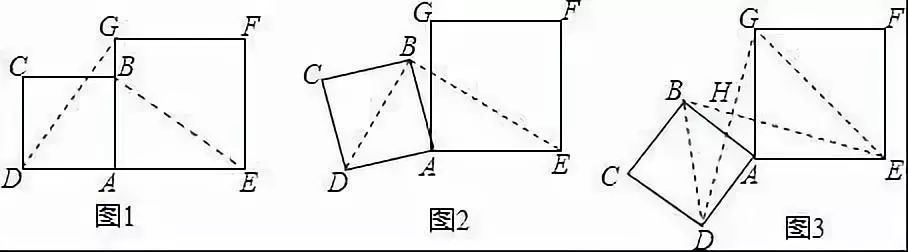
例1 在数学兴趣小组活动中,小明进行数学探究活动,将边长为2的正方形ABCD与边长为2的正方形AEFG按图1位置放置,AD与AE在同一直线上,AB与AG在同一直线上.
(1)小明发现DG⊥BE,请你帮他说明理由.
(2)如图2,小明将正方形ABCD绕点A逆时针旋转,当点B恰好落在线段DG上时,请你帮他求出此时BE的长.
(3)如图3,小明将正方形ABCD绕点A继续逆时针旋转,线段DG与线段BE将相交,交点为H,写出△GHE与△BHD面积之和的最大值,并简要说明理由。
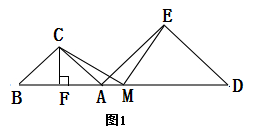
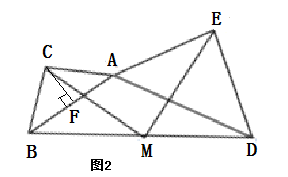
例2 现有两个具有一个公共顶点的等腰直角三角形△ADE和△ABC,其中∠ACB和∠AED=90°,且AC=BC,AE=DE,CF⊥AB于F,M为线段BD中点,连接CM,EM.
(1)如图1,当A、B、D在同一条直线上时,若AC=1,AE=2,求FM的长度;
(2)如图1,当A、B、D在同一条直线上时,求证:CM=EM;
(3)如图2,当A、B、D在同一条直线上时,请探究CM,EM的数量关系和位置关系,请先给出结论,然后证明。

连载 · 《新概念一》教程连载Lesson35-36(打印版)
片区学区确定后应在一段时期内保持相对稳定!
2018年沈阳市中小学学区划分方案
巴黎圣母院被大火严重损毁,这些家乡百年古迹也正在消失
奔驰事件给孩子最好的启示:做人,要有掀桌子的能力,更有不掀桌子的修养
视频 · 最新!奔驰对涉事4S店出手!和解协议达成
巴黎圣母院大火后,圆明园官方发声!网友:大国风范!
声明:本公众号所有文章均由壮壮爸爸编辑整理,部分资料来源于网络,版权归原作者所有。转载请申请授权并标明准确出处!否则,本公众号将使用媒体监督和法律诉讼的手段,追究一切侵权责任!

最后
以上就是善良树叶最近收集整理的关于n条直线相交最多有几个邻补角_初中数学 2019中考数学必备:相交线与平行线+矩形、菱形、正方形的5大考点及题型汇总(全)...的全部内容,更多相关n条直线相交最多有几个邻补角_初中数学内容请搜索靠谱客的其他文章。








发表评论 取消回复