【Matlab】信号的生成实验

57 阅读 0 评论 38 点赞

我是靠谱客的博主矮小凉面，最近开发中收集的这篇文章主要介绍【Matlab】信号的生成实验，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

前言

一个信号系统课程中使用Matlab产生实指数信号、正弦信号、复指数信号、阶跃信号、高斯函数的实验并简要分析。

一、函数表达式

实指数信号：
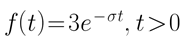
正弦信号：
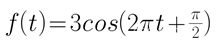
复指数信号：
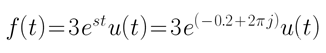
阶跃信号：
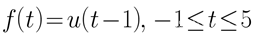
高斯函数：

二、Matlab实现及分析

2.1 实指数信号

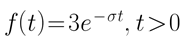
实指数信号表达式
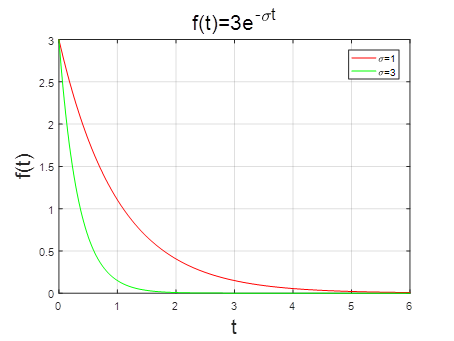
该信号为衰减信号，是时间t的函数，参数为sigma。

% f(t)=Aexp(-sigma*t),t>0
f=@(t,A,sigma)(A*exp(-sigma*t));  % 函数定义
t=0:0.01:6;
y0=f(t,3,1);
y1=f(t,3,3);
plot(t,y0,'r');
plot(t,y1,'g');
grid on;hold on;
xlabel('t','Fontsize',20);
ylabel('f(t)','Fontsize',20);
title('f(t)=3e^{-sigmat}','Fontsize',20);
legend('sigma=1','sigma=3');      % 曲线标注

如图1所示，衰减程度受sigma影响，sigma越大衰减越快。
图 1 实指数信号

2.2 正弦信号

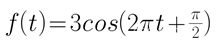
正弦信号表达式
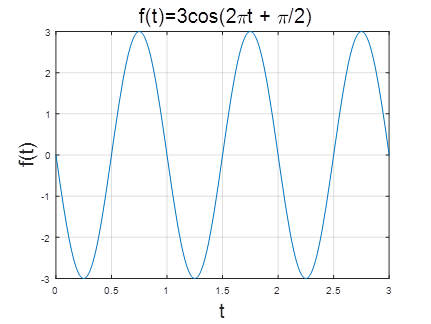
该信号为周期信号，是时间t的余弦函数，幅值为3，周期T为1，omega为2pi。

% f(t)=Acos(w*t+theta)
A=3;
omega=2 * pi;
theta=pi/2;
t=0:0.01:3 * 2 * pi / omega;
y=A*cos(omega*t+theta);
plot(t,y);
grid on;  % 网格
xlabel('t','Fontsize',20);
ylabel('f(t)','Fontsize',20);
title(' f(t)=3cos(2pit + pi/2)','Fontsize',20);

如图2所示，其震荡程度受omega影响，omega越大震荡的频率越高。
图 2 正弦信号

2.3 复指数信号

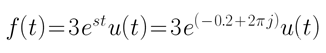
复指数信号表达式
该信号是一个复函数，由欧拉公式可得
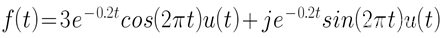
在这里插入图片描述
复指数信号在二维平面无法展示全部内容，故使用三维空间绘制，其在x-y平面的投影即是虚部，在x-z平面的投影就是实部。

%f(t)=Aexp(st)u(t)
%=Aexp(sigmat+jwt)u(t)
%=Aexp(sigma*t)cos(w*t)u(t)+jexp(sigma*t)sin(w*t)u(t)
A=3;
omega=2*pi;
sigma=-0.2;
s=sigma+1j*omega;
t=0:0.01:8*2*pi/omega;
f=A*exp(s*t);  
L=length(t);
x=t;y=imag(f);z=real(f);
y_0=zeros(size(t));     % 获取y=0的点集
y_1=ones(size(t));
z_0=zeros(size(t));
z_1=ones(size(t));
plot3(x,y,z,'b');  % 复指数函数图像的点
plot3(x,y_0,z_0,'k');       % x轴的线
hold on;grid on;
x1=[x;x];
y1=[y;y_0];
z1=[z;z_0];
for i=1:L   % 图像上的点对应的连线
    plot3(x1(:,i),y1(:,i),z1(:,i),'b');
end
% x-y
plot3(x,y,-A*z_1,'.y');     % x-y平面投影的点
y2=[y;y_0];
z2=[-A*z_1;-A*z_1];
for i=1:L   % x-y平面投影的线
    plot3(x1(:,i),y2(:,i),z2(:,i),'y');
end
plot3(x,A*y_1,z,'r');     % x-z平面投影的线
y3=[A*y_1;A*y_1];
z3=[z;z_0];
for i=1:L   % x-z平面投影的线
	plot3(x1(:,i),y3(:,i),z3(:,i),'r');
end
y_e=A*exp(sigma*x);
y_e2=-y_e;
plot(x,y_e,x,y_e2);    % 包络线
xlabel('自变量','Fontsize',16);
ylabel('虚部','Fontsize',16);
zlabel('实部','Fontsize',16);
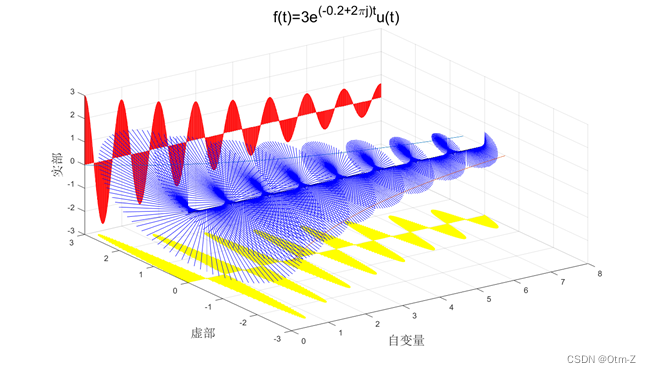
title('f(t)=3e^{(-0.2+2pij)t}u(t)','Fontsize',20);

如图3所示，在x-y和x-z的投影分别是虚部和实部。该信号是衰减的，随时间t的增大，幅值越小。
图 3 复指数信号

2.4 阶跃信号

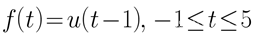
阶跃信号表达式
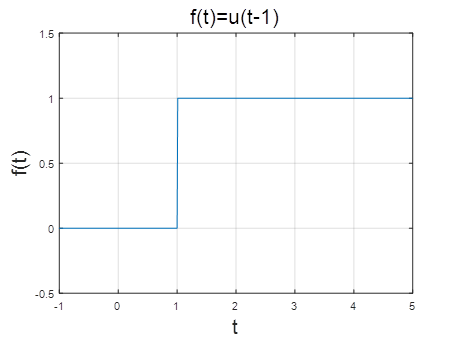
该函数一个跳变函数，定义域为[-1,5]。
阶跃信号u(t)表示当t > 0时f(x)为1，否则为0，根据条件不难绘制出u(t-1)的图像。

% f(t)=u(t-1), -1<=t<=5
t=-1:0.01:5;
y=(t>1);
plot(t,y);
grid on;
xlabel('t','Fontsize',20);
ylabel('f(t)','Fontsize',20);
title('f(t)=u(t-1)','Fontsize',20);
axis([-1 5 -0.5 1.5])    % 设置坐标轴

如图4所示，f(t)是u(t)向右时移1的阶跃信号，当t>1时为1，否则为0。
图 4 阶跃信号

2.5 高斯函数

高斯函数表达式
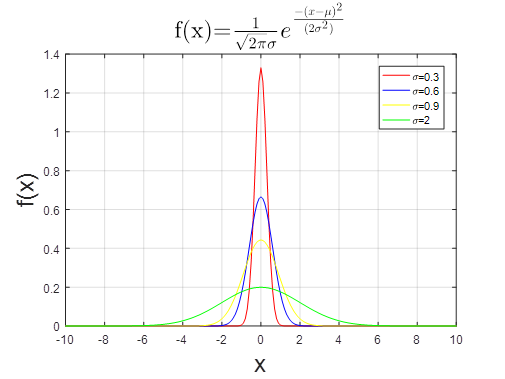
也是正态分布函数，定义域为(-∞<x<+∞)，均值为mu，方差为sigma

% f(t)=1/(sqrt(2*pi)*sigma)*exp(-(x-mu).^2/(2*sigma^2))
Gaussian=@(x,mu,sigma)(1/(sqrt(2*pi)*sigma)*exp(-(x-mu).^2/(2*sigma^2)));
x = -10:0.1:10;
y0 = Gaussian(x,0,0.3);
y1 = Gaussian(x,0,0.6);
y2 = Gaussian(x,0,0.9);
y3 = Gaussian(x,0,2);
plot(x,y0,'r');hold on;
plot(x,y1,'b');hold on;
plot(x,y2,'y');hold on;
plot(x,y3,'g');
grid on;    %网格
xlabel('x','Fontsize',20);
ylabel('f(x)','Fontsize',20);
title('f(x)=$frac{1}{sqrt{2pi}sigma}e^{frac{-(x-mu)^2}{(2sigma^2)}}$','interpreter','latex','Fontsize',20);
legend('sigma=0.3','sigma=0.6','sigma=0.9','sigma=2');  % 曲线标注

若令mu为0得到如图5所示的图像，x=mu就是函数图像的对称轴，该函数的方差sigma越大图像越“矮胖”，方差越小图像越“高瘦”，且定义域上函数的积分恒等于1，即
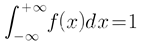
在这里插入图片描述
图 5 高斯函数