概述
离散时间基本信号
信号与系统的本科课程学习与考试主要涉及且应该掌握的离散时间基本信号为：复指数序列、单位阶跃序列、矩形序列、斜变序列、单位样值序列。
一、复指数序列
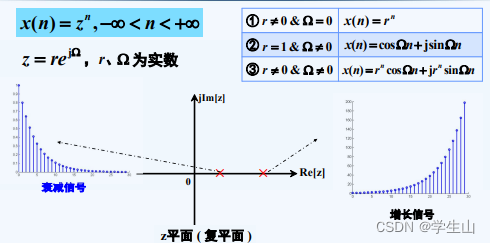
二、单位阶跃序列
性质与连续时间的单位阶跃信号一致。
1.单边特性
2.表示信号的作用区间
三、矩形序列
又名窗函数序列。
R
N
(
n
)
=
{
1
0
≤
n
≤
N
−
1
0
e
l
s
e
R_N(n)=left{begin{aligned} &1quad 0leq nleq N-1\&0quad else end{aligned}right.
RN(n)={10≤n≤N−10else
便于记忆，简而言之：是4就只到3。
四、斜变序列
n
u
(
n
)
=
{
n
n
≥
0
0
n
<
0
nu(n)=left{begin{aligned}nquad n geq 0\0quad n<0end{aligned}right.
nu(n)={nn≥00n<0
五、单位样值序列
δ
(
n
)
=
{
1
n
=
0
0
n
≠
0
delta(n)=left{begin{align*} &1quad n=0 \ &0quad n neq 0 end{align*}right.
δ(n)={1n=00n=0
又名单位脉冲序列。性质与连续时间的单位冲激信号一致。
1.筛选特性：
x
(
n
)
δ
(
n
−
n
0
）
=
x
(
n
0
)
δ
(
n
−
n
0
)
x(n) delta(n-n_{0}）= x(n_{0}) delta(n-n_0)
x(n)δ(n−n0）=x(n0)δ(n−n0)
2. 取样特性：
∑
n
=
−
∞
∞
x
(
n
)
δ
(
n
−
n
0
)
=
x
(
n
0
)
sum_{n = -infty}^{infty}x(n) delta(n-n_0)=x(n_0)
n=−∞∑∞x(n)δ(n−n0)=x(n0)
和矩形序列的差分累加关系：
δ
(
n
)
=
u
(
n
)
−
u
(
n
−
1
)
u
(
n
)
=
∑
k
=
−
∞
∞
δ
(
k
)
begin{align*} delta(n) &= u(n)-u(n-1)\ u(n) &= sum_{k = -infty}^{infty} delta(k) end{align*}
δ(n)u(n)=u(n)−u(n−1)=k=−∞∑∞δ(k)
最后
以上就是沉默大象为你收集整理的信号与系统_离散时间基本信号离散时间基本信号的全部内容，希望文章能够帮你解决信号与系统_离散时间基本信号离散时间基本信号所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
发表评论 取消回复