前言
就一个NN而言,包含梯度、偏置、参数更新,而前面第一篇博客学习了theano中符号变量的定义, 第二篇博客学习了变量的随机初始化, 变量之间的互相操作(类似于
sigmoid(w∗x+b)
), 但是参数更新还应涉及到损失函数的偏导计算,这一章节就是看看theano的梯度计算函数`tensor.grad(). 此外还有雅可比式(一阶导),海森矩阵(二阶导),雅克比乘以向量,海森矩阵乘以向量的操作
梯度计算
目前感觉这个函数没什么需要注意的, 使用方法直接就是 T.grad(y,x), 意思就是y对x求导,而且我们还能用function.marker.fgraph.outputs[0]把得到的导数公式输出出来,先导入模块,没什么好说的
import theano
import theano.tensor as T
from theano import pp#用于输出表达式拿
y=x^2+x^3+x^4试水x=T.dscalar('x')#定义一个变量 y=x**2+x**3+x**4#定义一个操作 gy=T.grad(y,x)#将y对x求导 f=theano.function([x],gy)# 执行这个求导函数 pp(f.maker.fgraph.outputs[0])输出是
Elemwise{Composite{((i0 * i1) + (i2 * sqr(i1)) + (i3 * Composite{(sqr(i0) * i0)}(i1)))}}(TensorConstant{2.0}, x, TensorConstant{3.0}, TensorConstant{4.0})然后怎么依据这个输出把导数表达式写出来呢?这里我们把
i0,i1,i2,i3分别用2,x,3,4替换(TensorConstant{2.0}意思就是常数张量2.0,’sqr’代表平方),然后带入到前面的Composite{((i0 * i1) + (i2 * sqr(i1)) + (i3 * Composite{(sqr(i0) * i0)}(i1)))}中, 注意遇到Composite{xxx}(xxx), 就用()中的xxx去替换{}中的xxx,然后我来分析一波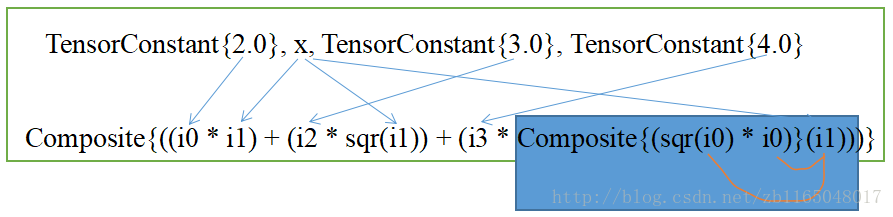
这样就能得到一个结果
2*x+3*x^2+4*(x^2)*x,刚好就是 y=x2+x3+x4 对 x 的偏导结果同样的例子套入到对率函数中去
y1=1/(1+T.exp(-x)) gy1=T.grad(y1,x) f2=theano.function([x],gy1) # pp(gy1) pp(f2.maker.fgraph.outputs[0])输出是
Elemwise{Composite{(scalar_sigmoid((-i0)) * scalar_sigmoid(i0))}}(x)按照上面的图画一下,然后可以写出来结果是
sigmoid(-x)*sigmoid(x),其实也就是
y∂y∂x=sigmoid(x)=11+e−x=sigmoid(−x)∗sigmoid(x)=11+e−x∗11+ex=y(1−y)
注意, T.grad()的第二个参数可以是一个列表,那么输出也就是列表了,意思应该就是损失函数可以对权重和偏置在一个函数中求导
计算雅克比矩阵
在theano中雅克比就是计算一个函数的输出相对于每个输入的一阶偏导数。theano中有两种方法去实现
间接(人工)方法
由于这需要使用到循环(对每个输入都要计算偏导数), 因而提前接触到了theano中用于创建循环的函数scan(), 如果想提前了解scan(), 可以去看这位博主的五个例子掌握theano.scan函数x=T.dvector('x') y=x**2 J,updates=theano.scan(lambda i,y,x : T.grad(y[i],x),sequences=T.arange(y.shape[0]),non_sequences=[y,x]) f=theano.function([x],J,updates=updates) f([4,4]) ``` array([[ 8., 0.], [ 0., 8.]]) ```这里稍微说一下用到的
scan内容:- 第一个参数默认就是定义的函数了,这里用了个
lambda表达式lambda i,y,x : T.grad(y[i],x)意思是我们要计算这个梯度, 而这i,y,x的来源就是后面的几个参数,赋值顺序一般是sequences中的变量,outputs_info的变量,non_sequences中的变量 , 这个顺序要记住 - 参数
sequences表示我们需要遍历的量,一般都是T.arange()创建的列表,把它丢给了i - 参数
non_sequences是其他两个输入量[y,x],把它丢给了lambda函数中的y,x - 返回值
J是输出变量列表,updates是字典,表示每个输出变量列表的更新规则
- 第一个参数默认就是定义的函数了,这里用了个
直接方法
theano中直接提供了一个函数来实现Jacobian矩阵的计算theano.gradient.jacobian(expression, wrt, consider_constant=None, disconnected_inputs='raise')#直接计算hessian矩阵 x=T.dvector('x') y=T.dvector('y') input=[x,y] s=T.sum(x**2+y**2) f=theano.gradient.jacobian(expression=s,wrt=input) h=theano.function(input,f) x=[1,2] y=[1,2] h(x,y) ''' [array([ 2., 4.]), array([ 2., 4.])] '''看样子计算的就是损失函数
expression关于input中变量的偏导数
计算海森矩阵
普遍接受的关于海森矩阵的数学说法是: 它是具有标量输出和向量输入的二阶偏导函数的矩阵。同样有间接和直接两种计算方法
间接(人工)计算方法
与间接计算Jacobian矩阵不同的是我们不是计算某个表达式的雅克比式,而是计算关于导数T.grad(cost,x)的雅可比式#间接计算Hessian矩阵 x=T.dvector('x') y=x**2 cost=y.sum() gy=T.grad(cost,x)#先计算损失关于x的梯度 H,updates=theano.scan(lambda i,gy,x : T.grad(gy[i],x),sequences=T.arange(gy.shape[0]),non_sequences=[gy,x]) f=theano.function([x],H,updates=updates) f([4,4]) ''' array([[ 2., 0.], [ 0., 2.]]) '''依旧是
theano.scan()的应用, 第一个参数是计算梯度的函数, 后面的先把sequences的列表丢给i, 然后将non_sequence中的gy,x分别丢给lambda表达式中的gy和x直接计算方法
theano中直接提供了一个函数来实现Hessian矩阵的计算:theano.gradient.hessian(cost, wrt, consider_constant=None, disconnected_inputs='raise')x=T.dvector('x') y=T.dvector('y') input=[x,y] s=T.sum(x**2+y**2) f=theano.gradient.hessian(cost=s,wrt=input) h=theano.function(input,f) x=[1,2] y=[1,2] h(x,y) ''' [array([[ 2., 0.], [ 0., 2.]]), array([[ 2., 0.], [ 0., 2.]])] '''看样子计算的就是损失函数
cost关于input中变量的偏导数
雅可比式与向量乘积
R-操作(右乘)
计算目标
其中 x 可以是矩阵或者是张量,主要还是因为我们需要依据权重矩阵做一些表达式的计算
#雅可比式*向量
W=T.dmatrix('W')
V=T.dmatrix('V')
x=T.dvector('x')
y=T.dot(x,W)
JV=T.Rop(y,W,V)#这里直接调用的就是Rop函数对应右乘操作
f=theano.function([W,V,x],JV)
w=[[1, 1], [1, 1]]
v=[[2, 2], [2, 2]]
x=[0,1]
f(w,v,x)
'''
array([ 2., 2.])
'''这干了一件什么事情呢?数学表达式如下:
L-操作(左乘)
#向量*雅可比式
W = T.dmatrix('W')
V = T.dvector('V')
x = T.dvector('x')
y = T.dot(x, W)
VJ = T.Lop(y, W, V)#这里直接调用的就是Rop函数对应右乘操作
f = theano.function([V,x], VJ)
f([2, 2], [0, 1])
'''
array([[ 0., 0.],
[ 2., 2.]])
'''
左乘和右乘的差别
其实从矩阵的乘法规则就能发现他们的不同:
左乘中的v与输出有相同的shape, 右乘中的v与输入有相同的shape。
左乘的结果与输入有相同shape, 右乘的结果与输出有相似的shape
海森矩阵与向量乘积
由于Hessian矩阵具有对成型, 所以有两种操作可以得到相同的结果,但是性能可能稍有不同。所以theano建议大家在使用两个方法时先分析一下
方法一:
x=T.dvector('x')
v=T.dvector('v')
y=T.sum(x**2)#定义操作
gy=T.grad(y,x)#一阶导
vH=T.grad(T.sum(gy*v),x)#利用一阶导得到二阶导
f=theano.function([x,v],vH)
f([4,4],[2,2])
'''
array([ 4., 4.])
'''方法二:
x=T.dvector('x')
v=T.dvector('v')
y=T.sum(x**2)#定义操作
gy=T.grad(y,x)#一阶导
Hv=T.Rop(gy,x,v)#利用Jacobian矩阵的右乘操作
f=theano.function([x,v],Hv)
f([4,4],[2,2])
'''
array([ 4., 4.])
'''注意事项
grad函数是符号运算: 接受和返回Theano变量grad可以被重复使用grad操作中, 标量损失可以直接用grad处理, 但是数组类型的需要用循环处理,比如计算Jacobian矩阵中需要对向量中每个值进行梯度的循环计算- 内置函数能够高效计算向量*雅可比式、向量*海森矩阵
代码地址:链接: https://pan.baidu.com/s/1eSAIZOu 密码: wu27
最后
以上就是尊敬机器猫最近收集整理的关于【theano-windows】学习笔记三——theano中的导数前言梯度计算计算雅克比矩阵计算海森矩阵雅可比式与向量乘积海森矩阵与向量乘积注意事项的全部内容,更多相关【theano-windows】学习笔记三——theano中内容请搜索靠谱客的其他文章。








发表评论 取消回复