P1113 杂务

81 阅读 0 评论 54 点赞

我是靠谱客的博主甜美小懒猪，最近开发中收集的这篇文章主要介绍P1113 杂务，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

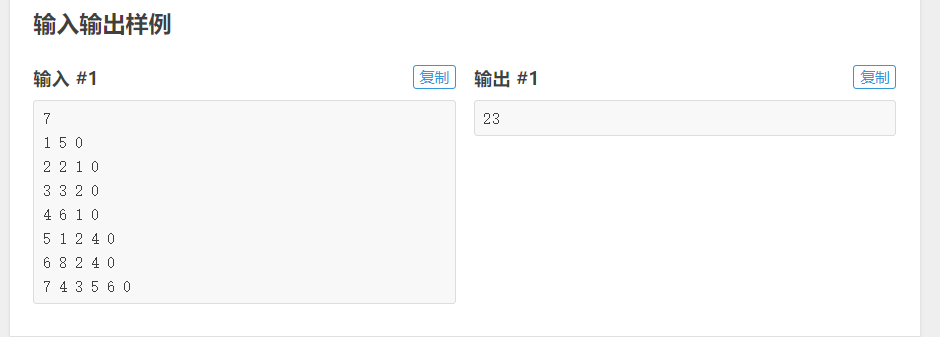
在这里插入图片描述

这道题是一道很好的拓扑排序入门题

样例中的图画出来长这样~

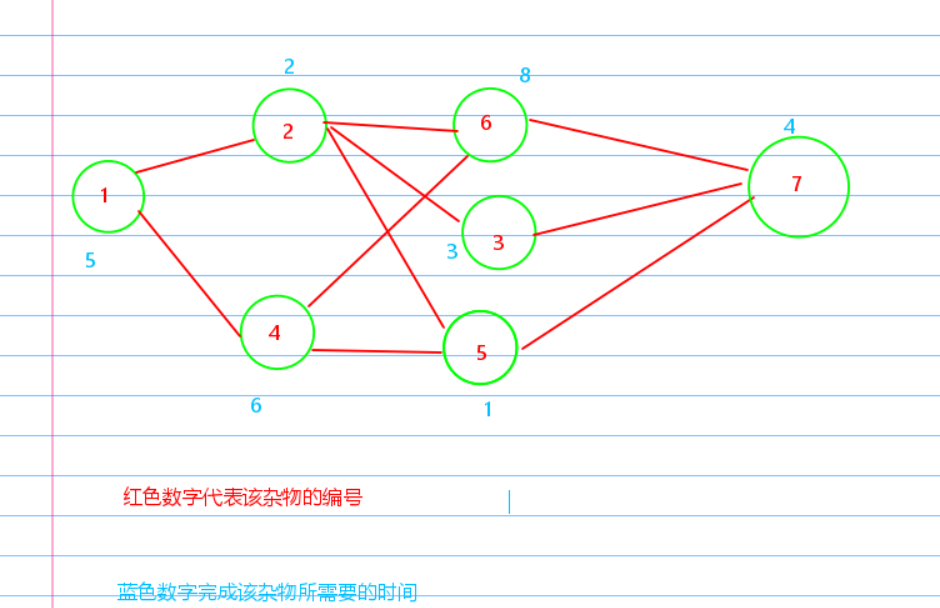
在这里插入图片描述
如图所示，我们可以这样考虑.

设dp[i],的意义为从i号节点出发路径的最大值

设int time[] 这个数组的意义是完成i号杂物所需要的时间

很显然 time[1]=5,time[2]=2,time[3]=3,time[4]=6,time[5]=1,time[6]=8,time[7]=4 ,这样依次赋值就行了

最后结果很显然就是 dp[1]=max(dp[2],dp[4])+time[1] ,这样所算出来的dp[1]，就是完成所有杂物所需要的时间。
状态转移方程.
dp[i]=max(dp[j],dp[k],…dp[z])+time[i]
max中的dp[j]------dp[z]是所有从i出去的边

也就是说我们要想求dp[i],必须先求出与他相连接的dp[j]—dp[k]

那么,如何保证一个节点在他的后继节点被访问之后才访问该节点呢，很显然就要用到逆的拓扑排序.

我们可以先通过递归来实现逆拓扑排序的过程.

我们用dfs来遍历，首先对于一个点i，设dp[i]表示从i号顶点出发的路径的最大值
dfs(i)返回的也是从i号顶点出发的路径的最大值

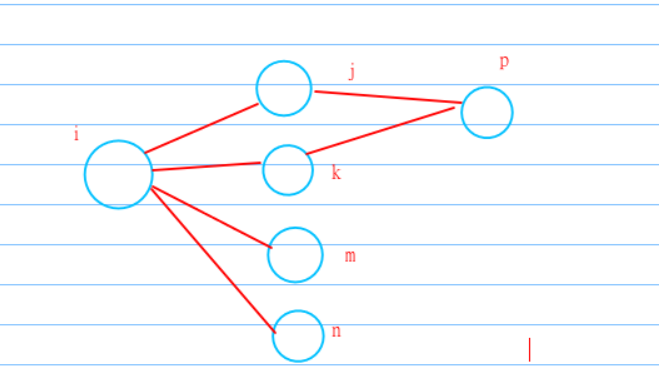
在这里插入图片描述
那么 dp[i]=max(dfs(j,k,m…n)+time[i],dp[i])

递归的结束条件是什么呢？？很显然，是当出度为0的时候,假设那个节点的编号是p,我们可以直接返回time[p]

,下面是AC代码~

#include<iostream>
#include <vector>
#include <cstring>
#define Max 10005
using namespace std;
vector<int > Graph[Max];
int t[Max];
int dp[Max];//i好顶点出发所能获得的最长路径
bool flag[Max];
int dfs(int i) ;//以定点i开始的最长路径
int Maxs=-1;
int main()
{

    int n,x,num;
    cin>>n;
    memset(flag,false, sizeof(flag));
    memset(dp,0, sizeof(dp));
    for(int i=1;i<=n;i++)
    {
        cin>>num; //输入编号,输入时间>>t[num];
        cin>>t[num];
        while(cin>>x&&x!=0)
        {
            Graph[x].push_back(num);
            flag[num]=true;
        }
    }
    for(int i=1;i<=n;i++)
    {
        if(!flag[i])
        {
           Maxs=max(Maxs,dfs(i)); //所有入度为0的顶点中路径最长的那一个
        }
    }
    cout<<Maxs<<endl;
    return 0;
}

int dfs(int i) //以定点i开始的最长路径
{
    if(dp[i])
    {
        return dp[i];
    }
    if(Graph[i].size()==0)
    {
        return dp[i]=t[i];
    }
    else
    {
        for(int j=0;j<Graph[i].size();j++)
        {
            int v=Graph[i][j];
            dp[i]=max(dp[i],dfs(v)+t[i]);
        }
    }
    return dp[i];
}

上面的代码实际上是一个逆的拓扑排序，因为递归有去有回，所以递归到末尾再返回，是一个逆的拓扑排序，下面就来介绍正的拓扑排序了~

设dp[i] 为以i结尾的最长路径

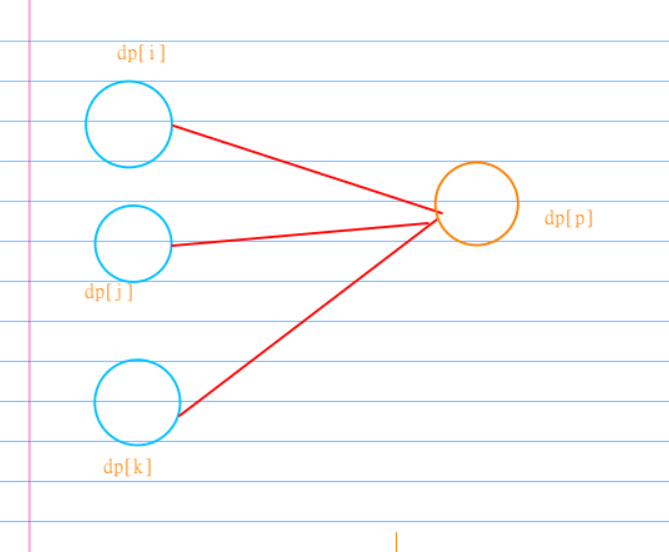
在这里插入图片描述
如图所示 dp[p]=max(dp[i],dp[j],dp[k])+time[p]

这里就变成了：我们访问一个节点的时候，要保证他所有的前驱节点都被访问了，也就是我们访问p节点的时候，要保证节点 i,j,k全部已经访问过了。

那么，按照拓扑排序的思路，我们初始化的时候，要把入度为0的节点 i 全部压入队列。并把这这些节点的dp值设置为dp[i]=time[i]
我们先设置一个数组记录每个节点的入度数 d[]
这样做好以后，我们按照拓扑排序的思路：从队列中弹出一个节点u，遍历这个弹出的节点u所有指向的节点v,首先将这个节点u所指向的节点v的入度值全部-1,也就是d[v]–（如果节点v的入度减到了0,d[v]==0，那就将这个节点加入队列。）然后我们开始更新dp的值，假设是i—>j，那么就是dp[j]=max(dp[i]+time[j],dp[j])

这样就可以将整个dp[i]的值全部求出来，我们只需要找出所有出度为0的节点v（i<=v<=n），dp[v]的最大值即可。

下面是AC代码~

#include<iostream>
#include <vector>
#include <cstring>
#include <queue>
#define Max 10005
using namespace std;
vector<int > Graph[Max];
int f(int n);
int d[Max];//记录入度数
int t[Max];//记录完成杂物i所需要的时间
int dp[Max];//以i号顶点结尾的最长路径
bool flag[Max];//筛选出度为0的节点
int Maxs=-1;
int main()
{
    int n,x,num;
    cin>>n;
    memset(flag,false, sizeof(flag));
    memset(dp,0, sizeof(dp));
    memset(d,0, sizeof(d));
    for(int i=1;i<=n;i++)
    {
        cin>>num; //输入编号,输入时间
        cin>>t[num];
        while(cin>>x&&x!=0)
        {
            Graph[x].push_back(num);
            d[num]++;
            flag[x]=true; //有出度的顶点都设置为true
        }
    }
    cout<<f(n)<<endl;
    return 0;
}

int f(int n)
{
    queue<int > que;
    for(int i=1;i<=n;i++)
    {
        if(!d[i]) //没有入度的顶点都设置为
        {
            que.push(i);
            dp[i]=t[i];//到达i号顶点所经历的最长路程
        }
    }
    while(!que.empty())
    {
        int j=que.front();
        que.pop();
        for(int i=0;i<Graph[j].size();i++)
        {
            int v=Graph[j][i];
            dp[v]=max(dp[v],dp[j]+t[v]);
            d[v]--;
            if(!d[v])
            {
                que.push(v);
            }
        }
    }
    for(int i=1;i<=n;i++)
    {
        if(!flag[i]) //出度为0的顶点
        {
            Maxs=max(dp[i],Maxs);
        }
    }
    return Maxs;
}