文章目录
- 简述
- 原理
- 康托展开
- 逆康托展开
- 示例:
- 应用
简述
康托展开是一个全排列到一个自然数的双射,常用于构建hash表时的空间压缩。设有n个数(1,2,3,4,…,n),可以有组成不同(n!种)的排列组合,康托展开表示的就是在n个不同元素的全排列中, 比当前排列组合小的个数,那么也可以表示当前排列组合在n个不同元素的全排列中的名次(当前的名次 = 比当前排列组合小的个数 + 1)。
原理
X=a[n]*(n-1)!+a[n-1]*(n-2)!+...+a[i]*(i-1)!+...+a[1]*0!
其中, a[i]为整数,并且0 <= a[i] <= i, 0 <= i < n, 表示当前未出现的的元素中排第几个,这就是康托展开。
例如有3个数(1,2,3),则其排列组合及其相应的康托展开值如下:
| 排列组合 | 名次 | 康托展开 | 值 |
|---|---|---|---|
| 123 | 1 | 0 * 2! + 0 * 1! + 0 * 0! | 0 |
| 132 | 2 | 0 * 2! + 1 * 1! + 0 * 0! | 1 |
| 213 | 3 | 1 * 2! + 0 * 1! + 0 * 0! | 2 |
| 231 | 4 | 1 * 2! + 1 * 1! + 0 * 0! | 3 |
| 312 | 5 | 2 * 2! + 0 * 1! + 0 * 0! | 4 |
| 321 | 6 | 2 * 2! + 1 * 1! + 0 * 0! | 5 |
比如其中的 231:
- 想要计算排在它前面的排列组合数目(123,132,213),则可以转化为计算比首位小即小于2的所有排列「1 * 2!」,首位相等为2并且第二位小于3的所有排列「1 * 1!」,前两位相等为23并且第三位小于1的所有排列(0 * 0!)的和即可,康托展开为:1 * 2!+1 * 1+0 * 0=3。
- 所以小于231的组合有3个,所以231的名次是4。
康托展开
再举个例子说明。
在(1,2,3,4,5)5个数的排列组合中,计算 34152的康托展开值。
- 首位是3,则小于3的数有两个,为1和2,a[5]=2,则首位小于3的所有排列组合为 a[5]*(5-1)!
- 第二位是4,则小于4的数有两个,为1和2,注意这里3并不能算,因为3已经在第一位,所以其实计算的是在第二位之后小于4的个数。因此a[4]=2
- 第三位是1,则在其之后小于1的数有0个,所以a[3]=0
- 第四位是5,则在其之后小于5的数有1个,为2,所以a[2]=1
- 最后一位就不用计算啦,因为在它之后已经没有数了,所以a[1]固定为0
- 根据公式:
X = 2 * 4! + 2 * 3! + 0 * 2! + 1 * 1! + 0 * 0! = 2 * 24 + 2 * 6 + 1 = 61
所以比 34152 小的组合有61个,即34152是排第62。
具体代码实现如下:(假设排列数小于10个)
static const int FAC[] = {1, 1, 2, 6, 24, 120, 720, 5040, 40320, 362880}; // 阶乘
int cantor(int *a, int n)
{
int x = 0;
for (int i = 0; i < n; ++i) {
int smaller = 0; // 在当前位之后小于其的个数
for (int j = i + 1; j < n; ++j) {
if (a[j] < a[i])
smaller++;
}
x += FAC[n - i - 1] * smaller; // 康托展开累加
}
return x; // 康托展开值
}
tips: 这里主要为了讲解康托展开的思路,实现的算法复杂度为O(n^2),实际当n很大时,内层循环计算在当前位之后小于当前位的个数可以用 线段树来处理计算,而不用每次都遍历,这样复杂度可以降为O(nlogn)。
逆康托展开
一开始已经提过了,康托展开是一个全排列到一个自然数的双射,因此是可逆的。即对于上述例子,在(1,2,3,4,5)给出61可以算出起排列组合为 34152。由上述的计算过程可以容易的逆推回来,具体过程如下:
- 用 61 / 4! = 2余13,说明a[5]=2,说明比首位小的数有2个,所以首位为3。
- 用 13 / 3! = 2余1,说明a[4]=2,说明在第二位之后小于第二位的数有2个,所以第二位为4。
- 用 1 / 2! = 0余1,说明a[3]=0,说明在第三位之后没有小于第三位的数,所以第三位为1。
- 用 1 / 1! = 1余0,说明a[2]=1,说明在第二位之后小于第四位的数有1个,所以第四位为5。
- 最后一位自然就是剩下的数2啦。
- 通过以上分析,所求排列组合为 34152。
具体代码实现如下:(假设排列数小于10个)
static const int FAC[] = {1, 1, 2, 6, 24, 120, 720, 5040, 40320, 362880}; // 阶乘
//康托展开逆运算
void decantor(int x, int n)
{
vector<int> rest; // 存放当前可选数,保证有序
for(int i=1;i<=n;i++)
v.push_back(i);
vector<int> ans; // 所求排列组合
for(int i=n;i>=1;i--)
{
int r = x % FAC[i-1];
int t = x / FAC[i-1];
x = r;
a.push_back(v[t]); // 剩余数里第t+1个数为当前位
v.erase(v.begin()+t); // 移除选做当前位的数
}
}
示例:
leetcode题目 60. 第k个排列
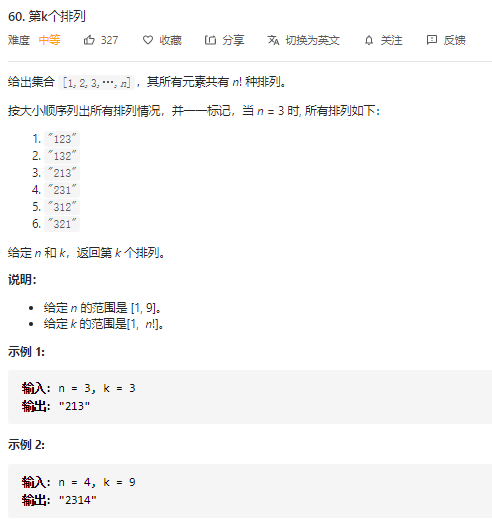
直接套逆康托展开即可,需要处理的是求的是第k个排列,那么其对应的康托展开值应该减1 (k - 1)。
class Solution {
public:
// 逆康托展开
string getPermutation(int n, int k) {
static constexpr int FAC[] = {1, 1, 2, 6, 24, 120, 720, 5040, 40320, 362880}; // 阶乘
vector<int> rest; // 存放当前可选数,有序
for(int i = 1;i <= n;i++)
rest.push_back(i);
k--; //要先 -1 才是其康托展开的值
string ans = "";
ans.reserve(n);
for(int i = n; i >= 1; i--)
{
int r = k % FAC[i-1];
int t = k / FAC[i-1];
k = r;
ans += to_string(rest[t]); // 剩余数里第t+1个数为当前位
rest.erase(rest.begin() + t); // 移除选做当前位的数
}
return ans;
}
};
应用
应用最多的场景也是上述讲的它的特性。
-
给定一个自然数集合组合一个全排列,所其中的一个排列组合在全排列中从小到大排第几位。
在上述例子中,在(1,2,3,4,5)的全排列中,34152的排列组合排在第62位。 -
反过来,就是逆康托展开,求在一个全排列中,从小到大的第n个全排列是多少。
比如求在(1,2,3,4,5)的全排列中,第62个排列组合是34152。[注意具体计算中,要先 -1 才是其康托展开的值。] -
另外康托展开也是一个数组到一个数的映射,因此也是可用于hash,用于空间压缩。比如在保存一个序列,我们可能需要开一个数组,如果能够把它映射成一个自然数, 则只需要保存一个整数,大大压缩空间。比如八数码问题。
最后
以上就是高兴大炮最近收集整理的关于康托展开和逆康托展开简述原理康托展开逆康托展开应用的全部内容,更多相关康托展开和逆康托展开简述原理康托展开逆康托展开应用内容请搜索靠谱客的其他文章。








发表评论 取消回复