The crowdedness of the discotheque would never stop our friends from having fun, but a bit more spaciousness won't hurt, will it?
The discotheque can be seen as an infinite xy-plane, in which there are a total of n dancers. Once someone starts moving around, they will move only inside their own movement range, which is a circular area Ci described by a center (xi, yi) and a radius ri. No two ranges' borders have more than one common point, that is for every pair (i, j) (1 ≤ i < j ≤ n) either ranges Ci and Cj are disjoint, or one of them is a subset of the other. Note that it's possible that two ranges' borders share a single common point, but no two dancers have exactly the same ranges.
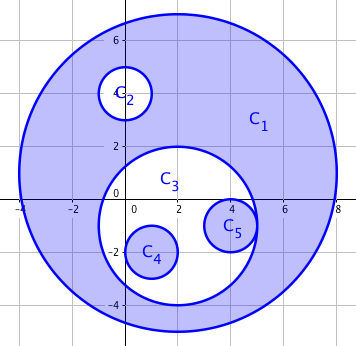
Tsukihi, being one of them, defines the spaciousness to be the area covered by an odd number of movement ranges of dancers who are moving. An example is shown below, with shaded regions representing the spaciousness if everyone moves at the same time.
But no one keeps moving for the whole night after all, so the whole night's time is divided into two halves — before midnight and after midnight. Every dancer moves around in one half, while sitting down with friends in the other. The spaciousness of two halves are calculated separately and their sum should, of course, be as large as possible. The following figure shows an optimal solution to the example above.

By different plans of who dances in the first half and who does in the other, different sums of spaciousness over two halves are achieved. You are to find the largest achievable value of this sum.
The first line of input contains a positive integer n (1 ≤ n ≤ 1 000) — the number of dancers.
The following n lines each describes a dancer: the i-th line among them contains three space-separated integers xi, yi and ri ( - 106 ≤ xi, yi ≤ 106, 1 ≤ ri ≤ 106), describing a circular movement range centered at (xi, yi) with radius ri.
Output one decimal number — the largest achievable sum of spaciousness over two halves of the night.
The output is considered correct if it has a relative or absolute error of at most 10 - 9. Formally, let your answer be a, and the jury's answer be b. Your answer is considered correct if 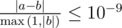 .
.
5 2 1 6 0 4 1 2 -1 3 1 -2 1 4 -1 1
138.23007676
8 0 0 1 0 0 2 0 0 3 0 0 4 0 0 5 0 0 6 0 0 7 0 0 8
289.02652413
The first sample corresponds to the illustrations in the legend.
题意:有很多人跳舞,跳舞范围是个圆,然后跳舞的人分上半夜和下半夜,同一个圈圈里面的人不能同时跳。让你把所有能跳圈圈的面积加起来,得到的面积最大
解题思路:把所有圈圈被覆盖的次数统计一下,最大那个肯定加,然后奇数大的加进去,偶数大的减掉,最大的可以在上半夜跳,然后奇数大的在下半夜跳
#include <iostream>
#include <cstdio>
#include <cstring>
#include <string>
#include <algorithm>
#include <queue>
#include <stack>
#include <cmath>
#include <map>
#include <bitset>
#include <set>
#include <vector>
#include <functional>
using namespace std;
#define LL long long
const int INF = 0x3f3f3f3f;
#define pi acos(-1)
int n;
double ans;
struct node
{
double x, y, r;
int flag;
}a[1001];
bool cmp(node a, node b)
{
if (a.r == b.r) return a.x == b.x ? a.y < b.y : a.x < b.x;
return a.r > b.r;
}
bool check(node a, node b)
{
return (a.x - b.x)*(a.x - b.x) + (a.y - b.y)*(a.y - b.y) < (a.r + b.r)*(a.r + b.r);
}
int main()
{
while (~scanf("%d", &n))
{
for (int i = 1; i <= n; i++) scanf("%lf%lf%lf", &a[i].x, &a[i].y, &a[i].r), a[i].flag = 0;
sort(a + 1, a + n + 1, cmp);
for (int i = 1; i < n; i++)
for (int j = i + 1; j <= n; j++)
if (check(a[i], a[j])) a[j].flag++;
for (int i = 1; i <= n; i++)
{
if (!a[i].flag) ans += a[i].r*a[i].r*pi;
else if (a[i].flag % 2) ans += a[i].r*a[i].r*pi;
else ans -= a[i].r*a[i].r*pi;
}
printf("%.8lfn", ans);
}
return 0;
}最后
以上就是危机篮球最近收集整理的关于Codeforces 814D-An overnight dance in discotheque的全部内容,更多相关Codeforces内容请搜索靠谱客的其他文章。








发表评论 取消回复