【DFS/BFS】NYOJ-58-最少步数（迷宫最短路径问题）

115 阅读 0 评论 76 点赞

我是靠谱客的博主复杂糖豆，最近开发中收集的这篇文章主要介绍【DFS/BFS】NYOJ-58-最少步数（迷宫最短路径问题），觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

【题目链接：NYOJ-58】

　　经典的搜索问题，想必这题用广搜的会比较多，所以我首先使的也是广搜，但其实深搜同样也是可以的。

　　不考虑剪枝的话，两种方法实践消耗相同，但是深搜相比广搜内存低一点。

　　我想，因为广搜需要的就是队列，所以相比递归队列更耗内存？

　　当然DFS并不像上图所说，需要用栈，而是运用递归即可。

BFS：

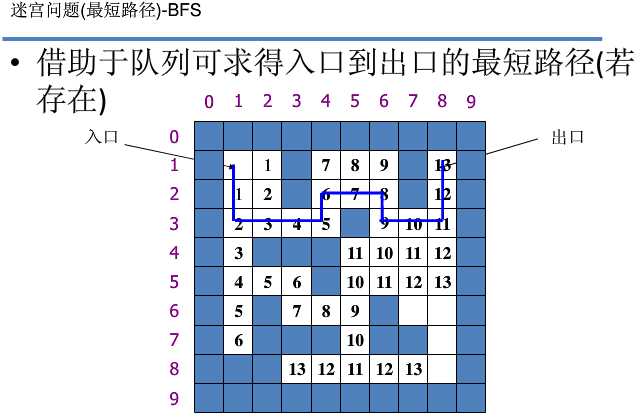
　　因为BFS是要一个接一个的遍历，所以用到了结构体，来保存坐标和当前所走步数

　　1.每走一步，通过定义的结构体，从队列中提取a（即上一步的坐标、步数（步数每次累加））

　　2.在a的基础上进行对a周围四个方向进行判断，找出可以继续走的位置（即非障碍、边界），并将该位置的坐标，进入队列中

　　继续走下一步时，循环以上1.2两步操作

 1 #include<iostream>
 2 #include<cstdio>
 3 #include<cstring>
 4 #include<algorithm>
 5 #include<queue>
 6 using namespace std;
 7 int dir[4][2]= {1,0,-1,0,0,1,0,-1};
 8 struct point{
 9
int x,y,step;
10 };
11 int bfs(point s,point e,int map[9][9]){
12
queue<point>tp;//自定义类型的队列 
13
int i;
14
point t;//保存当前坐标 ，临时变量
15
//s表示之前
16
//e表示目标 
17
s.step=0;//保存步数 
18
map[s.x][s.y]=1;//标记此处已经走过 
19
tp.push(s);//初始化队列 ，s中(x,y)初始为起始坐标，step = 0 
20
while(!tp.empty()){//循环直至队列为空 
21
s=tp.front();//每次循环s都等于队首 
22
tp.pop();//删除队首 
23
if(s.x==e.x&&s.y==e.y)//如果当前坐标与目标坐标相等
24
return s.step;
//返回当前的步数
25
//遍历四个不同的方向
26
//如果是通道（0），即增加步数 
27
for(int i=0; i<4; i++){
28
t.x=s.x+dir[i][0];
29
t.y=s.y+dir[i][1];
30
if(map[t.x][t.y]==0){//如果是通道 
31
t.step=s.step+1;
32
map[t.x][t.y]=1;//标记此处已经走过，及标记为墙 
33 
tp.push(t);
34 
}
35 
}
36 
}
37 }
38 int main(){
39
int t;
40
scanf("%d",&t);
41
while(t--){
42 
point s,e;
43
int map[9][9]= {1,1,1,1,1,1,1,1,1,
44
1,0,0,1,0,0,1,0,1,
45
1,0,0,1,1,0,0,0,1,
46
1,0,1,0,1,1,0,1,1,
47
1,0,0,0,0,1,0,0,1,
48
1,1,0,1,0,1,0,0,1,
49
1,1,0,1,0,1,0,0,1,
50
1,1,0,1,0,0,0,0,1,
51
1,1,1,1,1,1,1,1,1,};
52
scanf("%d%d%d%d",&s.x,&s.y,&e.x,&e.y);
53
printf("%dn",bfs(s,e,map));
54 
}
55
return 0;
56 }

DFS:

　　DFS就没什么好说了，不明白可以看看之前的DFS博客

　　只不过这里，没有用到单独的二维数组see[][]，来判断本个坐标是已经搜索过

　　而是结合题意，把当前所在位置变为'1'，即障碍、边界，那么在递归往下延伸判断四周时，达到同样的目的

　　当然在DFS函数最后，需要把Map[][]重新变为'0'，因为递归执行的顺序是自上而下再从下向上返回

　　因为是多组测试数据，所以需要在递归返回时，把迷宫“恢复原貌”

#include<iostream>
using namespace std;
#define min(a,b) a < b ? a : b
int Map[9][9] = {1,1,1,1,1,1,1,1,1,
1,0,0,1,0,0,1,0,1,
1,0,0,1,1,0,0,0,1,
1,0,1,0,1,1,0,1,1,
1,0,0,0,0,1,0,0,1,
1,1,0,1,0,1,0,0,1,
1,1,0,1,0,1,0,0,1,
1,1,0,1,0,0,0,0,1,
1,1,1,1,1,1,1,1,1,};
int a,b,c,d,num;
void dfs(int x,int y,int s){
if(Map[x][y]) return;
if(x == c && y == d){
num = min(s,num);
return;
}
s++;
Map[x][y] = 1;
dfs(x - 1,y,s);
dfs(x + 1,y,s);
dfs(x,y - 1,s);
dfs(x,y + 1,s);
Map[x][y] = 0;
}
int main(){
int n;
cin >> n;
while(n--){
num = 10000;
cin >> a >> b >> c >> d;
dfs(a,b,0);
cout << num << endl;
}
return 0;
}