HDU 5628 Clarke and math（Dirchlet卷积+快速幂）

Description
给出f(i)，i=1,2,…,n，求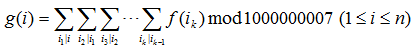
Input
第一行一正整数T表示用例组数，每组用例首先输入一正整数n表示f序列长度，之后n个整数f(i)（1<=T<=5,n<=100000,0<=f(i) < 1e9+7）
Output
对于每组用例，输出g(1),g(2),…,g(n)
Sample Input
2
6 2
2 3 3 3 3 3
23 3
2 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
Sample Output
2 7 7 15 7 23
2 9 9 24 9 39 9 50 24 39 9 102 9 39 39 90 9 102 9 102 39 39 9
Solution
首先介绍Dirchlet卷积：定义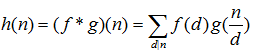为f和g的Dirchlet卷积，其性质如下：
1.交换律：f*g=g*h
2.结合律：f*(g*h)=(f*g)*h
3.分配律：f*(g+h)=f*g+f*h
4.存在幺元e使得e*f=f：e(1)=1,e(i)=0,i!=1
在此题中令h=1，那么g=f*1*1*…1（k个1），由交换律可以用快速幂进行logk次卷积求出1^k=1*1*1…*1，之后再对f和1^k做一遍卷积即可得到答案，时间复杂度O(nlognlogk)
Code

#include<cstdio>
#include<iostream>
#include<cstring>
using namespace std;
typedef long long ll;
#define maxn 111111
#define mod 1000000007ll
int T,n,k;
ll f[maxn],x[maxn],ans[maxn],temp[maxn];
void Dirichlet(ll *a,ll *b)
{
memset(temp,0,sizeof(temp));
for(int i=1;i*i<=n;i++)
{
temp[i*i]=(temp[i*i]+a[i]*b[i]%mod)%mod;
for(int j=i+1;i*j<=n;j++)
temp[i*j]=(temp[i*j]+a[i]*b[j]%mod+a[j]*b[i]%mod)%mod;
}
for(int i=1;i<=n;i++)b[i]=temp[i];
}
int main()
{
scanf("%d",&T);
while(T--)
{
scanf("%d%d",&n,&k);
for(int i=1;i<=n;i++)scanf("%I64d",&f[i]),x[i]=1,ans[i]=0;
ans[1]=1;
while(k)
{
if(k&1)Dirichlet(x,ans);
Dirichlet(x,x);
k>>=1;
}
Dirichlet(f,ans);
for(int i=1;i<=n;i++)
printf("%I64d%c",ans[i],i==n?'n':' ');
}
return 0;
}

最后

以上就是娇气心情为你收集整理的HDU 5628 Clarke and math（Dirchlet卷积+快速幂）的全部内容，希望文章能够帮你解决HDU 5628 Clarke and math（Dirchlet卷积+快速幂）所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。