#（树上背包/多叉树上的背包问题）洛谷P1273 有线电视网（ 提高+/省选-）树形dp（分组背包）

题目描述

某收费有线电视网计划转播一场重要的足球比赛。他们的转播网和用户终端构成一棵树状结构，这棵树的根结点位于足球比赛的现场，树叶为各个用户终端，其他中转站为该树的内部节点。

从转播站到转播站以及从转播站到所有用户终端的信号传输费用都是已知的，一场转播的总费用等于传输信号的费用总和。

现在每个用户都准备了一笔费用想观看这场精彩的足球比赛，有线电视网有权决定给哪些用户提供信号而不给哪些用户提供信号。

写一个程序找出一个方案使得有线电视网在不亏本的情况下使观看转播的用户尽可能多。

输入格式

输入文件的第一行包含两个用空格隔开的整数N和M，其中2≤N≤3000，1≤M≤N-1，N为整个有线电视网的结点总数，M为用户终端的数量。

第一个转播站即树的根结点编号为1，其他的转播站编号为2到N-M，用户终端编号为N-M+1到N。

接下来的N-M行每行表示—个转播站的数据，第i+1行表示第i个转播站的数据，其格式如下：

K A1 C1 A2 C2 … Ak Ck

K表示该转播站下接K个结点(转播站或用户)，每个结点对应一对整数A与C，A表示结点编号，C表示从当前转播站传输信号到结点A的费用。最后一行依次表示所有用户为观看比赛而准备支付的钱数。

输出格式

输出文件仅一行，包含一个整数，表示上述问题所要求的最大用户数。

输入输出样例

输入 #1复制

5 3
2 2 2 5 3
2 3 2 4 3
3 4 2

输出 #1复制

2

说明/提示

样例解释

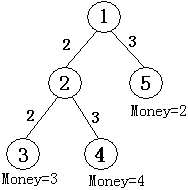
如图所示，共有五个结点。结点①为根结点，即现场直播站，②为一个中转站，③④⑤为用户端，共M个，编号从N-M+1到N，他们为观看比赛分别准备的钱数为3、4、2，从结点①可以传送信号到结点②，费用为2，也可以传送信号到结点⑤，费用为3（第二行数据所示），从结点②可以传输信号到结点③，费用为2。也可传输信号到结点④，费用为3（第三行数据所示），如果要让所有用户（③④⑤）都能看上比赛，则信号传输的总费用为：

2+3+2+3=10，大于用户愿意支付的总费用3+4+2=9，有线电视网就亏本了，而只让③④两个用户看比赛就不亏本了。

 思考：

从下往上分析，对于所有叶节点的父节点，从根节点到达该父节点的最大价值为：父节点到叶节点的路线权值xi，叶节点的价值yi，也就是max∑(yi-xi);

任意的叶节点选择，使父节点价值最大化（连通尽可能多地儿子），同时保证不亏本，需要存储该节点剩余的最大钱数

这样状态就出来了，

f[i][j]表示以i为父节点，剩余钱数为j的最大儿子数---1

或者f[i][j]表示以i为父节点，存在j个儿子的剩余钱数---2

试着推推1：

对于i的状态，设其儿子为ai，f[i][j]=max(f[i][j],f[ai][j+path[i][a[i]]]);

对于所有叶子节点i,f[i][money[i]]=1;

推推2：

初始化：对于所有叶子节点i,f[i][1]=money[i];

f[i][j]=max(f[i][j],f[i][j-k]+f[ai][k]);

正解：

树形dp（分组背包）

说一下自己的理解

1.明确dp[i][j]含义，表示i节点，选j个用户，能得到的钱的最大值，然后对每个节点做分组背包。

2.怎么看出是分组背包？首先，背包的总容量相当于该点为根节点的子树中所有的用户数量（dp[i][j]的 j 不可能超过它连接的所有用户数）。然后，把该节点的每个儿子看成一组，每组中的元素为选一个，选两个...选n个用户。

3.转移方程 dp[i][j]=max(dp[i][j],dp[i][j-k]+dp[v][k]-这条边的花费) i,j不解释了，v表示枚举到这一组（即i的儿子），k表示枚举到这组中的元素：选k个用户。

4.最后输出dp[1][i]>=0的i的最大值，所以反向枚举。

AC代码：

#include<iostream>
#include<cstdio>
#include<cstring>
#define For(i,a,b) for(int i=a;i<=b;i++)//简化代码
#define maxn 3001
using namespace std;
int n,m;
int dp[maxn][maxn],val[maxn];
inline int max(int x,int y)//手写max、min函数
{
return x>y?x:y;
}
inline int min(int x,int y)
{
return x<y?x:y;
}
inline int read()//读入优化
{
char ch;
while((ch=getchar())<'0' || ch>'9');
int res=ch-48;
while((ch=getchar())>='0'&&ch<='9')
res=res*10+ch-'0';
return res;
}
struct node{//邻接表，不赘述
int next;
int to;
int w;
};
node e[maxn*2+10];
int head[maxn*2+10],num;
void addedge(int from,int to,int weight)
{
e[++num].next=head[from];
e[num].to=to;
e[num].w=weight;
head[from]=num;
}
int dfs(int u)//最重要的dp函数，对节点u进行处理，返回节点u的最大客户个数
{
if(u>n-m)//如果节点u为叶子节点，也就是客户端口
{
dp[u][1]=val[u]; //那么最多只能提供一个客户，存在价值val[u]
return 1;//返回客户个数为1
}
int sum=0,t;//sum统计u节点的最大客户个数（也即是分组背包的容量）,t存储
//当前儿子节点的客户个数，将所有儿子分类，遍历其所有儿子进行分组背包
for(int i=head[u];i;i=e[i].next)//所有儿子，也就是分组背包的所有类别
{
int v=e[i].to; //
t=dfs(v);//求出该儿子组的容量
sum+=t;//统计总容量
for(int j=sum;j>0;j--)//分组背包，外层枚举背包体积
{
for(int k=1;k<=t;k++)//内层枚举儿子组的情况
//其实还可以进行二进制优化诶！
if(j-k>=0) //如果可以从该该儿子转移过来
dp[u][j]=max(dp[u][j],dp[u][j-k]+dp[v][k]-e[i].w);
}//那么更新值为u节点存j-k个客户，加上v节点提供的k个客户，减掉
//路费即可！
}
return sum;//返回
}

int main()
{
memset(dp,~0x3f,sizeof(dp));//dp数组赋成极小值
n=read(),m=read();
For(i,1,n-m)
{
int size=read();
For(j,1,size)//读边
{
int v=read(),w=read();
addedge(i,v,w);

}
}
For(i,n-m+1,n)//读客户端口
val[i]=read();
For(i,1,n)
dp[i][0]=0;
dfs(1);
for(int i=m;i>=1;i--)
if(dp[1][i]>=0)//第一个不亏本的，满足有最多的客户！
{
printf("%d",i);//输出即可！
break;
}

return 0;
}

多叉树上的背包问题：

https://blog.csdn.net/no1_terminator/article/details/77824790

https://blog.csdn.net/qq_30802053/article/details/78154266

https://blog.csdn.net/u013582254/article/details/78409114