关联博文
数据结构之Map基础入门与详解
认真学习Java集合之HashMap的实现原理
认真研究HashMap的读取和存放操作步骤
认真研究HashMap的初始化和扩容机制
认真研究JDK1.7下HashMap的循环链表和数据丢失问题
认真研究HashMap中的平衡插入
认真研究HashMap的结点移除
前文我们分析了HashMap的结点移除,本文我们继续分析结点移除后的树的平衡化。
下面方法入参中的x表示replacement,可能是移除的结点本身,也可能是移除的结点的后继结点的right结点或者是pr/pl。该方法返回最终的root结点。
从如下代码可知,进入balanceDeletion方法前交换后颜色的 P结点一定是黑色。以X=SR为例,那么也就是XP颜色为黑色。
TreeNode<K,V> r = p.red ? root : balanceDeletion(root, replacement);
比如下图是红黑树的一部分,这里X本质就是SR传入balanceDeletion方法的replacement中。
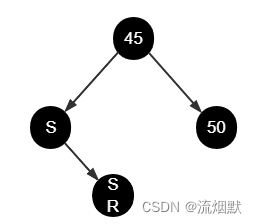
需要提前说明的是,在removeTreeNode方法中,当replacement != p 时 ,比如sr pl pr,会进行P结点的割离。当replacement ==p时,此时还没有进行树结点的割离。比如下图所示P结点(或者说与P结点的后继结点交换后的图示)没有左右结点,此时replacement ==p

以下代码&注释转载自博文红黑树的结点删除后平衡
/**
* 红黑树删除节点后,平衡红黑树的方法
*
* @param root 根节点
* @param x 节点删除后,替代其位置的节点,这个节点可能是一个节点,也可能是一棵平衡的红黑树,在此处就当作一个节点,在该节点以上部分需要自平衡
* @return 返回新的根节点
*/
static <K, V> HashMap.TreeNode<K, V> balanceDeletion(HashMap.TreeNode<K, V> root, HashMap.TreeNode<K, V> x) {
/**
* 进入这个方法,说明被替代的节点之前是黑色的,如果是红色的不会影响黑色高度,黑色的会影响以其作为根节点子树的黑色高度
* xp-父节点,xpl-父节点的左孩子,xpr-父节点的右孩子节点
* 注意:
* 进入该方法的时候 替代节点可能与删除节点相等:x == replacement == p
* 替代节点可能与删除节点不相等:x == replacement != p
*/
for (HashMap.TreeNode<K, V> xp, xpl, xpr; ; ) {
/**
* 1、x == null,当 replacement == p 时,删除节点不存在,返回;
* 因为当 replacement != p 时,replacement 肯定不会为null.在移除节点的方法中有三个地方对 replacement 进行赋值。
* 1、if (sr != null) replacement = sr;
* 2、if (pl != null) replacement = pl;
* 3、if (pr != null) replacement = pr;
* 2、x == root,如果替代完成后,该节点就是整棵红黑树的根节点,本身就是平衡的,直接返回
*/
if (x == null || x == root)
return root;
else if ((xp = x.parent) == null) {
// 如果父节点为空,说明当前节点就是根节点,设置根节点的颜色为黑色,返回
x.red = false;
return x;
} else if (x.red) {
/**
* 被替换节点(删除节点)的颜色是黑色的,删除之后黑色高度减1,如果替换节点是红色,将其设置为黑色,可以保证
* 1、与替换之前的黑色高度相等
* 2、满足红黑树的所有特性
* 达到平衡返回
*/
x.red = false;
return root;
/**
* 如果替换节点是黑色的,替换之前的节点也是黑色的,替换之后,以替换节点作为根节点子树黑色高度减少1,需要进行相关的自平衡操作
* 1、替换节点是父节点的左孩子
*/
// 前提是X为黑色,左侧分支
} else if ((xpl = xp.left) == x) {
/**
* 情况1、父节点的右孩子(兄弟节点)存在且为红色
* 处理方式:兄弟节点变黑,父节点变红,以父节点为支点进行左旋,重新获取兄弟节点,继续参与自平衡
*/
if ((xpr = xp.right) != null && xpr.red) {
xpr.red = false;
xp.red = true;
root = rotateLeft(root, xp);
// 重新获取XPR
xpr = (xp = x.parent) == null ? null : xp.right;
}
// 不存在兄弟节点,x指向父节点,向上调整
if (xpr == null)
x = xp;
else {
// sl-兄弟节点的左孩子,sr-兄弟节点的右孩子
HashMap.TreeNode<K, V> sl = xpr.left, sr = xpr.right;
/**
* 情况2-1:兄弟节点存在,且两个孩子的颜色均为黑色
* 1、sr == null || !sr.red:兄弟的右孩子为黑色(空节点的颜色其实也是黑色)
* 2、sl == null || !sl.red:兄弟的左孩子为黑色(空节点的颜色其实也是黑色)
* 处理方式:兄弟节点为红色,替换节点指向父节点,继续参与自平衡
*/
if ((sr == null || !sr.red) && (sl == null || !sl.red)) {
xpr.red = true;
x = xp;
} else {
/**
* 该条件综合评价为:兄弟节点的右孩子为黑色
* 1、sr == null:兄弟的右孩子为黑色(空节点的颜色其实也是黑色)
* 2、!sr.red:兄弟节点的右孩子颜色为黑色
*/
if (sr == null || !sr.red) {
/**
* sl != null:兄弟的左孩子是存在且颜色是红色的
* 情况2-2、兄弟节点右孩子为黑色、左孩子为红色
* 处理方式:兄弟节点的左孩子设为黑色,兄弟节点设为红色,以兄弟节点为支点进行右旋,重新设置x的兄弟节点,继续参与自平衡
*/
if (sl != null)
sl.red = false;
xpr.red = true;
root = rotateRight(root, xpr);
xpr = (xp = x.parent) == null ? null : xp.right;
}
/**
* 情况2-3、兄弟节点的右孩子是红色
* 处理方式:
* 1、如果兄弟节点存在,兄弟节点的颜色设置为父节点的颜色
* 2、兄弟节点的右孩子存在,颜色设为黑色
* 3、如果父节点存在,将父节点的颜色设为黑色
* 4、以父节点为支点进行左旋
*/
if (xpr != null) {
xpr.red = (xp == null) ? false : xp.red;
if ((sr = xpr.right) != null)
sr.red = false;
}
// 父节点不为空
if (xp != null) {
xp.red = false;
root = rotateLeft(root, xp);
}
// 替换节点指向根节点,平衡完成
x = root;
}
}
} else {
// X为黑色 右侧分支
/**
* 替换节点是父节点的右孩子节点
* 情况1、兄弟节点存在且为红色
* 处理方式:兄弟节点变黑,父节点变红,以父节点为支点进行左旋,重新获取兄弟节点,继续参与自平衡
*/
if (xpl != null && xpl.red) {
xpl.red = false;
xp.red = true;
root = rotateRight(root, xp);
xpl = (xp = x.parent) == null ? null : xp.left;
}
// 不存在兄弟节点,x指向父节点,向上调整
if (xpl == null)
x = xp;
else {
// sl-兄弟节点的左孩子,sr-兄弟节点的右孩子
HashMap.TreeNode<K, V> sl = xpl.left, sr = xpl.right;
/**
* 情况2-1:兄弟节点存在,且两个孩子的颜色均为黑色
* 1、sr == null || !sr.red:兄弟的右孩子为黑色(空节点的颜色其实也是黑色)
* 2、sl == null || !sl.red:兄弟的左孩子为黑色(空节点的颜色其实也是黑色)
* 处理方式:兄弟节点为红色,替换节点指向父节点,继续参与自平衡
*/
if ((sl == null || !sl.red) && (sr == null || !sr.red)) {
xpl.red = true;
x = xp;
} else {
/**
* 该条件综合评价为:兄弟节点的左孩子为黑色
* 1、sr == null:兄弟的左孩子为黑色(空节点的颜色其实也是黑色)
* 2、!sr.red:兄弟节点的左孩子颜色为黑色
*/
if (sl == null || !sl.red) {
/**
* sl != null:兄弟的右孩子是存在且颜色是红色的
* 情况2-2、兄弟节点左孩子为黑色、右孩子为红色
* 处理方式:兄弟节点的右孩子设为黑色,兄弟节点设为红色,以兄弟节点为支点进行左,重新设置x的兄弟节点,继续参与自平衡
*/
if (sr != null)
sr.red = false;
xpl.red = true;
root = rotateLeft(root, xpl);
xpl = (xp = x.parent) == null ? null : xp.left;
}
/**
* 情况2-3、兄弟节点的左孩子是红色
* 处理方式:
* 1、如果兄弟节点存在,兄弟节点的颜色设置为父节点的颜色
* 2、兄弟节点的左孩子存在,颜色设为黑色
* 3、如果父节点存在,将父节点的颜色设为黑色
* 4、以父节点为支点进行右旋
*/
if (xpl != null) {
xpl.red = (xp == null) ? false : xp.red;
if ((sl = xpl.left) != null)
sl.red = false;
}
if (xp != null) {
xp.red = false;
root = rotateRight(root, xp);
}
// 替换节点指向根节点,平衡完成
x = root;
}
}
}
}
}
最后
以上就是闪闪盼望最近收集整理的关于认真研究HashMap中的平衡删除的全部内容,更多相关认真研究HashMap中内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供,作为学习参考使用,或来自网络收集整理,版权属于原作者所有。








发表评论 取消回复