DP动态规划之背包问题(一)

115 阅读 0 评论 76 点赞

我是靠谱客的博主勤奋音响，最近开发中收集的这篇文章主要介绍DP动态规划之背包问题(一)，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

01背包问题

有n个重量和价值分别为w_i,v_i的物品。从这些物品中挑选出总重量不超过W的物品，求所有挑选方案中价值总和的最大值,每件物品只可以挑选一次。

输入
n=4
(w,v)={(2,3),(1,2),(3,4),(2,2)}
W=5
输出
7

最朴素的递归求解

#include<iostream>
using namespace std;
int *w,*v;//物品的重量，价值
int n;//物品的个数
int Rec(int i,int weight)//是否选取第i个物品
{
 int res;
 if(i==n)//物品已经选取完毕
   res=0;
 else if(weight<w[i])//第i个物品重量大于剩余重量weight
   res=Rec(i+1,weight);
 else
    res=max(Rec(i+1,weight),Rec(i+1,weight-w[i])+v[i]);//比较选取第i个物品和不选第i个物品的情况
 return res;
}
int main()
{
int W;//物品最大重量
cin>>n>>W;
w=new int[n];
v=new int[n];
for(int i=0;i<n;i++)
  cin>>w[i]>>v[i];
cout<<Rec(0,W);
return 0;
}

改进后

由上述代码可知，只要Rec函数的参数一样返回的结果就一样，可能会出现重复计算的可能
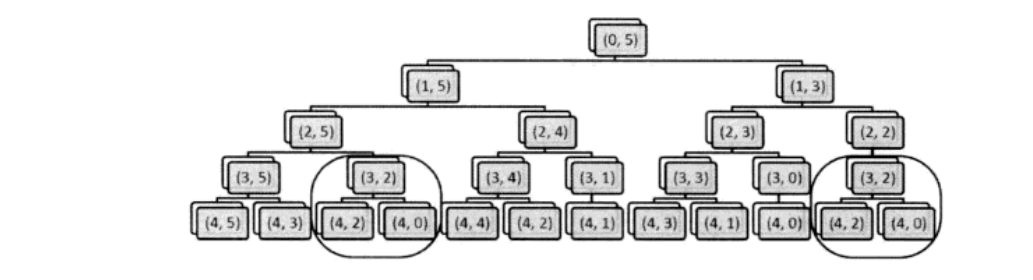
在这里插入图片描述
所以引入一个dp数组用来存储已经计算过的Rec(前i个物品重量不超过j的最大价值)。

#include<iostream>
#include<string.h> 
#define MAX 10
using namespace std;
int *w,*v;//物品的重量，价值
int n;//物品的个数
int dp[MAX][MAX];
int Rec(int i,int weight)//是否选取第i个物品
{
 if(dp[i][weight]>=0)//>=0表示已经计算过 
    return dp[i][weight];
 int res;
 if(i==n)//物品已经选取完毕
   res=0;
 else if(weight<w[i])//第i个物品重量大于剩余重量weight
   res=Rec(i+1,weight);
 else
    res=max(Rec(i+1,weight),Rec(i+1,weight-w[i])+v[i]);//比较选取第i个物品和不选第i个物品的情况
 return dp[i][weight]=res;
}
int main()
{
int W;//物品最大重量
memset(dp,-1,sizeof(dp));//初始化dp数组所有值为-1，表示未计算过 
cin>>n>>W;
w=new int[n];
v=new int[n];
for(int i=0;i<n;i++)
  cin>>w[i]>>v[i];
cout<<Rec(0,W);
return 0;
}

再作改进

根据上面的dp记忆化数组的定义可知，dp[i][j]表示，从第i个物品开始选取总重量不大于j的物品的价值最大值，它的递推关系式也可导出，
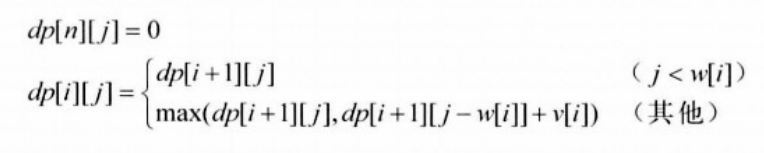
在这里插入图片描述
所以可以将上面改进过的算法再作一点改进(虽然算法复杂度是一样的，但是会很简洁)

void solve()
{
 for(int i=n-1;i>=0;i--)
  for(int j=0;j<=W;j++)
  {
   if(j<w[i])
    dp[i][j]=dp[i+1][j];
   else
    dp[i][j]=max(dp[i+1][j],dp[i+1][j-w[i]]+v[i]);
  }
  cout<<dp[0][W];
}

01背包问题变种

最后改进的代码是以物品的重量为变量进行动态规划，但是一旦物品的重量很大，那么该算法的复杂度就会大大增加，现在就重量较大，价值较小的问题来进行解决，将DP的对象改为价值。
dp[i+1][j]代表前i个物品价值为j的最小重量，由此可以得到关于dp的递推关系式：

dp[0][0]=0
dp[0][j]=INF,不存在这种情况，所以赋予一个足够大的值
dp[i+1][j]=min(dp[i][j],dp[i][j-v[i]]+w[i])/dp[i][j]

于是由递推关系式就可以解决该问题

#include<iostream>
#define Max_v 10
#define Max_n 10
#define Max 10
#define INF 50
using namespace std;
int dp[Max][Max_n*Max_v];
int n;
int W;
int *w,*v;
void solve()
{
for(int i=0;i<n;i++)
 for(int j=0;j<Max_n*Max_v;j++)
 {
  if(j<v[i])
   dp[i+1][j]=dp[i][j];
  else
   dp[i+1][j]=min(dp[i][j],dp[i][j-v[i]]+w[i]);
 }
 int tmp;
 for(int i=0;i<Max_n*Max_v;i++)
   if(dp[n][i]<=W)
     tmp=i;
  cout<<tmp;
}
int main()
{
dp[0][0]=0;
for(int i=1;i<Max_n*Max_v;i++)
  dp[0][i]=INF;
cin>>n>>W;
w=new int[n];
v=new int[n];
for(int i=0;i<n;i++)
  cin>>w[i]>>v[i];
solve();
return 0;
}