排序算法之快速排序

      相信大家也经常听到一种排序算法叫做“快排”，而且这也是很多同学经常用到的(一旦掌握了之后)，因为在大家的认知中，快速排序是在平均情况下性能最好的一种排序算法，他的时间复杂度较优并且没有额外的空间开销。下面就来简单介绍一下快速排序的整体思路和实现过程，其实本篇博文只是自己的一个笔记而已，给大家推荐https://bbs.codeaha.com/thread-4419-1-1.html，这个网址，从学习的角度来说，他的讲解是我见过的最易懂的一种版本。好了，接下来谈一谈我自己对快速排序的认识。

      快速排序他的巧妙在于将分治体现的很好，每一次二分都找到某个基准数，这个基准数可以随机选择，然后想方设法将大于基准数的元素放到左侧，把小于基准数的元素放在右边，然后将左右两边进行分别排序，而他的快也是体现在这个分治的思想里面，策略类似于我们搜索中的二分搜索。前面说了解决也比较虚，下面还是用个例子来说明一下。

首先我们用头部元素作为基准数，然后弄两个下标 i 和 j，如下图

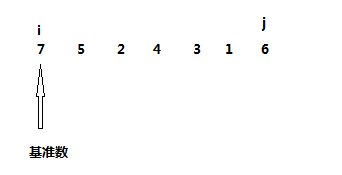
然后让 j 从右边开始找，找比基准数小的数（为什么要找比基准数小的呢?因为我们前面说过，基准数右边的数应该比他大，所以出现小的就是违规，所以应该找到并把它换到左边去），从上面的例子我们可以看到数字6比基准数小，找到6之后，j 就停顿一下，然后 i 出发，找比基准数大的数，显而易见一直到与 j 碰头都找不到比基准数大的，那么 i 就停顿在与 j 碰头的地方，然后把基准数与i j 碰头的地方元素交换一下，即交换 7 和 6，结果变成了下图

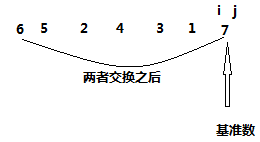
然后开始进行二分，分成两个区域进行排序，一个是从0 --- i ，一个是从 i ----len-1。回到上面的例子，我们发现i  j 碰头的地方就是len -1，那么显而易见不需要再对这一部分进行排序，我们只对0---- i进行排。此时我们依旧选择第一个数6作为基准数，然后重复以上步骤，如下图

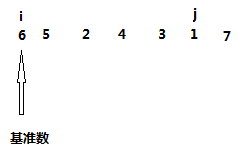
然后又是j 从右往左走，发现1比基准数小然后 j 停顿，接下来 i 从左往右走，一直到 i j碰头，还是没有发现比基准数大的元素，因此就执行下一步，将基准数与下标为 i  的元素交换，得到下面结果

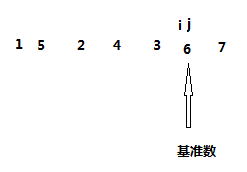
接下来进行二分，但是发现 i j 碰头的右边又是已经没有元素可以二分了，因此从执行左边的二分。将队首元素1作为基准数，然后重复上面步骤

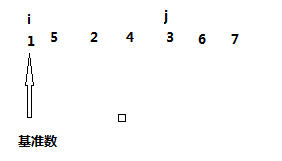
发现 j 从右往左走，都没有找到比 基准数小的元素，知道 i j 碰头，i j 碰头之后就进行基准数和 i 下标元素的交换，然后进行二分排序。如下图

后面发现 i j 碰头位置的左边已经没有元素可以排序了，因此进行右边的排序，如下图

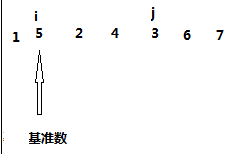
然后在重复上面的步骤，最后得到一个升序队列

关于这个过程我特别说明一下，这个初始序列是我随便想的一个顺序，我没想到他每一轮的执行结果都是那么的差，在我这个例子里面并没有很好的体现快速排序的优越性。但是在广大的随机数据序列中，快速排序的性能综合来说还是挺好的，只是我这个地方恰好命中了快排的最差的情况，时间复杂度退化成为了O(n*n)。

另外，有一个问题抛给大家思考，为什么我每次都要让 j 下标先走，而不是 i 下标先走，大家可以想一下。

下面附上源代码

void quick_sort(int *arr,int start,int end)
{
	int i=start;
	int j=end-1;
	if(j<=i)return;
	int tmp=arr[start];
	while(j>i)
	{
		for(;j>i;j--)
		{
			if(arr[j]<tmp)break;
		}
		for(;j>i;i++)
		{
			if(arr[i]>tmp)break;
		}
		swap(arr[i],arr[j]);
	}
	swap(arr[start],arr[i]);
	quick_sort(arr,start,i);
	quick_sort(arr,i+1,end);
}
//平均时间复杂度O(n*log n)

----------------------------有疑问可以联系我-----------------------------

最后

以上就是英俊小蘑菇为你收集整理的排序算法之快速排序的全部内容，希望文章能够帮你解决排序算法之快速排序所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。