目录
1、二进制
2、布尔逻辑
3、NOT
4、AND
5、OR
6、XOR
今天我们开始讲"抽象",不用管底层细节,把精力用来构建更复杂的系统。
1、二进制
上一讲,我们讲了计算机最早是机电设备,一般用十进制计数——比如用齿轮数来代表十进制,再到晶体管计算机。幸运的是,只用 开/关 两种状态也可以代表信息,这叫 二进制——意思是"用两种状态表示"。就像自行车有两个轮,双足动物有两条腿,你可能觉得两种状态不多,你是对的!但如果只需要表示 true 和 false,两个值就够了。电路闭合,电流流过,代表 "真";电路断开,无电流流过,代表"假",二进制也可以写成 1 和 0 而不是 true 和 false——只是不同的表达方式罢了——我们下一讲会讲更多细节。
晶体管的确可以不只是 开/关,还可以让不同大小的电流通过,一些早期电子计算机是三进制的,有 3 种状态,甚至五进制,5 种状态。问题是,状态越多,越难区分信号——如果手机快没电了或者附近有电噪音,因为有人在用微波炉,信号可能会混在一起...
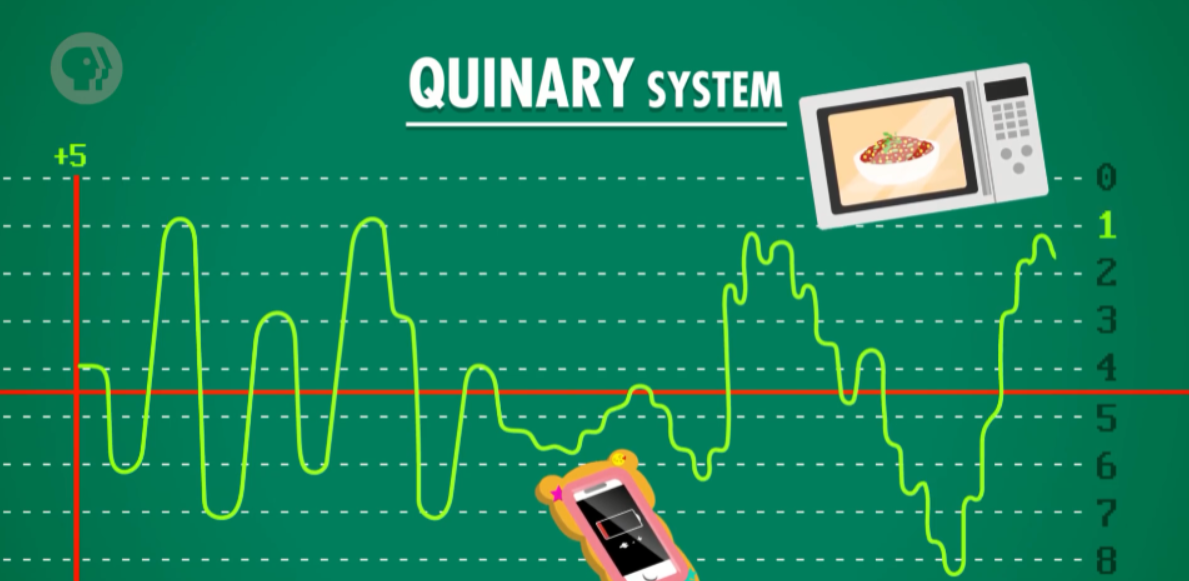
而每秒百万次变化的晶体管会让这个问题变得更糟!所以我们把两种信号尽可能分开——只用"开"和"关"两种状态,可以尽可能减少这类问题。
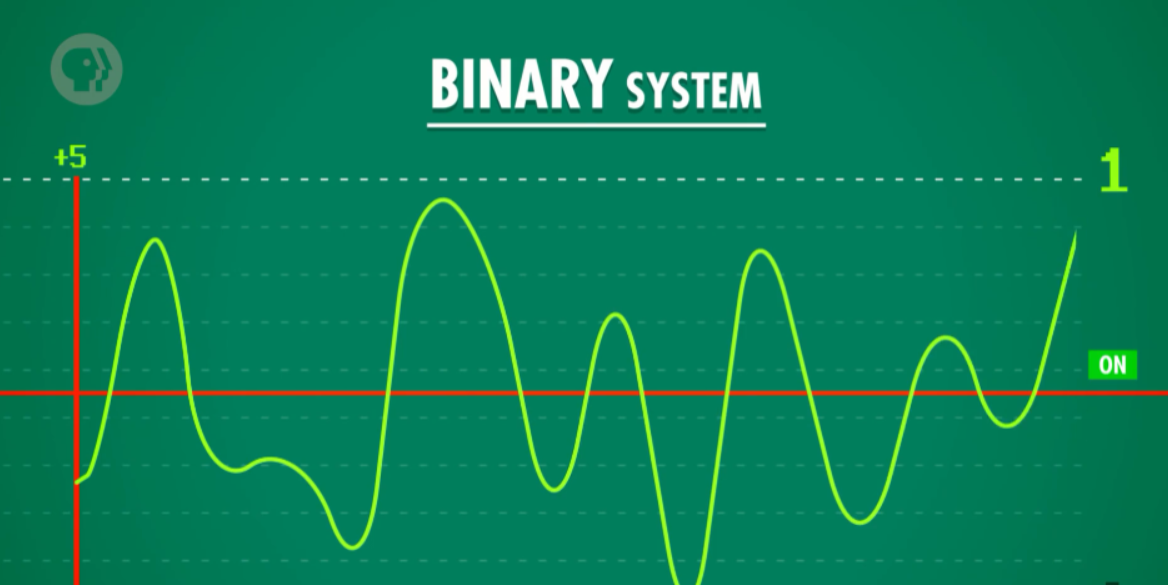
2、布尔逻辑
计算机用二进制的另一个原因是有一整个数学分支存在,专门处理"真"和"假",它已经解决了所有法则和运算,叫"布尔代数"!乔治·布尔(George Boole)是布尔二字的由来,是一位 19 世纪自学成才的英国数学家,他有兴趣用数学式子 扩展亚里士多德基于哲学的逻辑方法。布尔用 逻辑方程 系统而正式的证明真理(truth)。他在 1847 年的第一本书"逻辑的数学分析"中介绍过,在"常规"代数里 - 你在高中学的那种 - 变量的值是数字,可以进行加法或乘法之类的操作。
但在布尔代数中,变量的值是 true 和 false,N 能进行逻辑操作。布尔代数中有三个基本操作:NOT, AND 和 OR,这些操作非常有用,我们一个个来看:
NOT 操作把布尔值反转,N把 true 进行 NOT 就会变成 false,反之亦然,我们可以根据 NOT 操作的输入和输出,做出这个表.
| INPUT | OUTPUT |
| TRUE | FALSE |
| FALSE | TURE |
酷的地方是 - 用晶体管可以轻松实现这个逻辑。上一讲说过,晶体管只是电控制的开关,有 3 根线:2 根电极和 1 根控制线,控制线通电时,电流就可以从一个电极流到另一个电极,就像水龙头一样- 打开水龙头,就有水流出来,关掉水龙头,就没水了。
可以把控制线,当做输入 ( input ) N 底部的电极,当做输出(output),所以 1 个晶体管,有一个输入和一个输出。如果我们打开输入(input on) N,输出也会打开(output on) N ,因为电流可以流过;如果关闭输入(input off) N ,输出也会关闭(output off)N ,因为电流无法通过。或者用布尔术语来说N 输入为 真,输出为 真,输入为 假 N 输出为 假,我们也可以把这个做成"真值表"。
| INPUT | OUTPUT |
| TRUE | TRUE |
| FALSE | FALSE |
3、NOT
这个电路没什么意思,因为它没做什么事——输入和输出是一样的。但我们可以稍加修改,实现 NOT。与其把下面那根线当做 输出,我们可以把 输出 放到上面,如果打开 输入,电流可以流过然后 "接地",输出就没有电流,所以输出是 off。如果用水来举例,就像家里的水都从一个大管子流走了,打开淋浴头一点水也没有。
如果输入是 on,输出是 off,
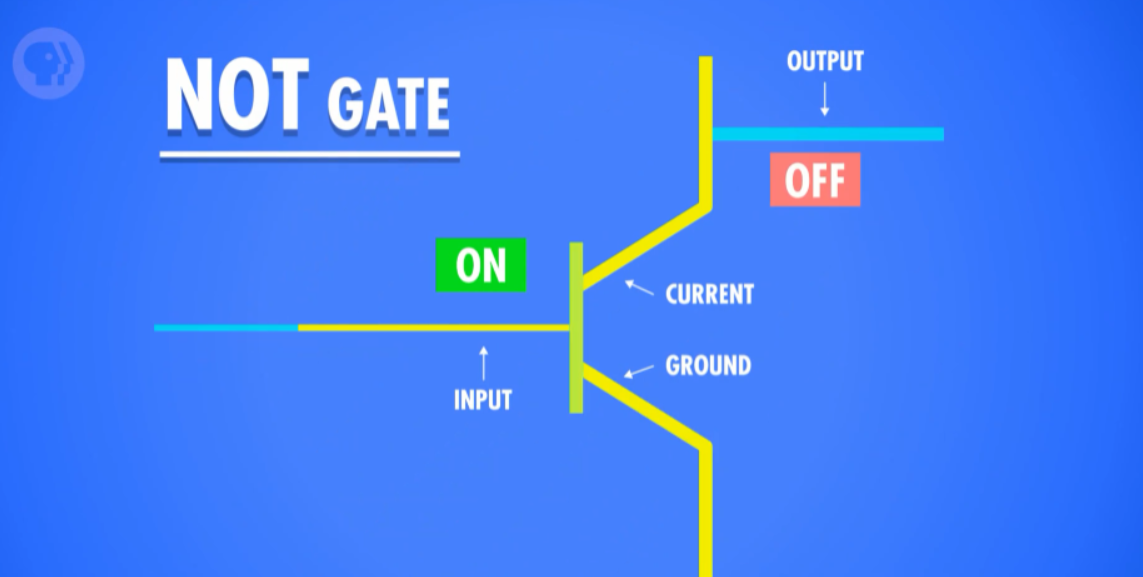
当输入是 off,电流没法接地,就流过了输出,所以输出是 on;
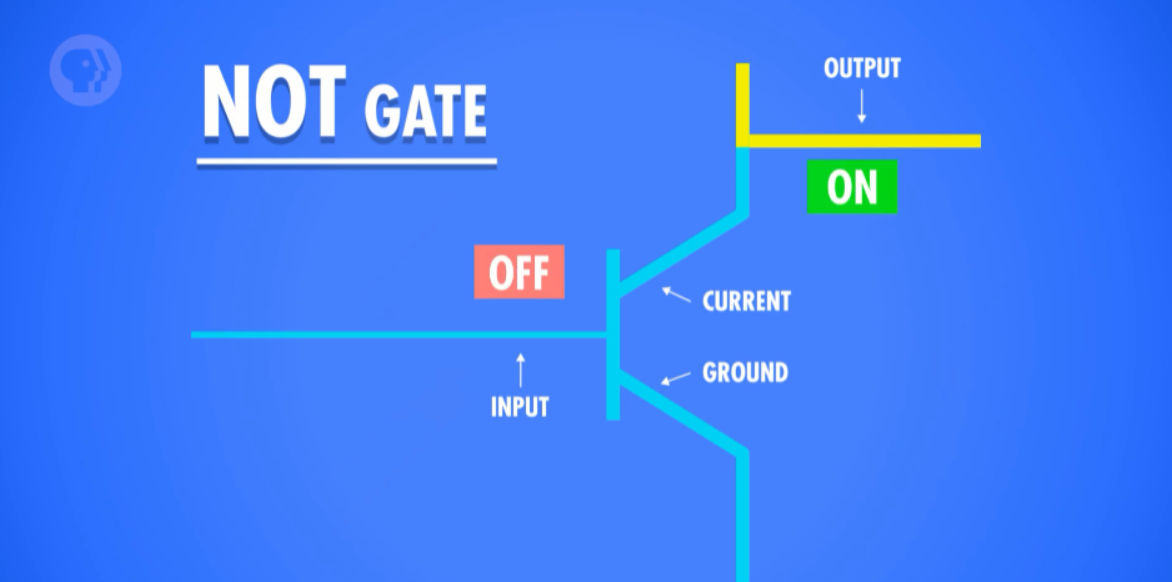
和 NOT 操作表一样!太棒了!我们做了个有点用的电路!我们叫它 "NOT 门" N ,之所以叫 "门",是因为它能控制电流的路径。
4、AND
"AND"操作有 2 个输入,1 个输出,如果 2 个输入都是 true,输出才是 true。你可以想成是 说真话,如果完全不说谎,才是诚实。举例,看如下这个句子,我叫 Carrie Anne "而且"我穿着蓝色的衣服,2 个都是真的,所以整个是真的。

但如果说,我叫 Carrie Anne"而且"我穿了裤子, 就是假的,因为我没穿裤子。

虽然前半句是真的,但是 真 "AND" 假,还是假,就算把前后顺序反过来,也依然是 假。如果我说 2 个假的事情,那么结果是假。和上次一样,可以给"AND"做个表
| INPUT A | INPUT B | OUTPUT |
| TRUE | TRUE | TRUE |
| TRUE | FALSE | FALSE |
| FALSE | TRUE | FLASE |
| FALSE | FALSE | FALSE |
为了实现 "AND 门",我们需要 2 个晶体管连在一起,这样有 2 个输入和 1 个输出。
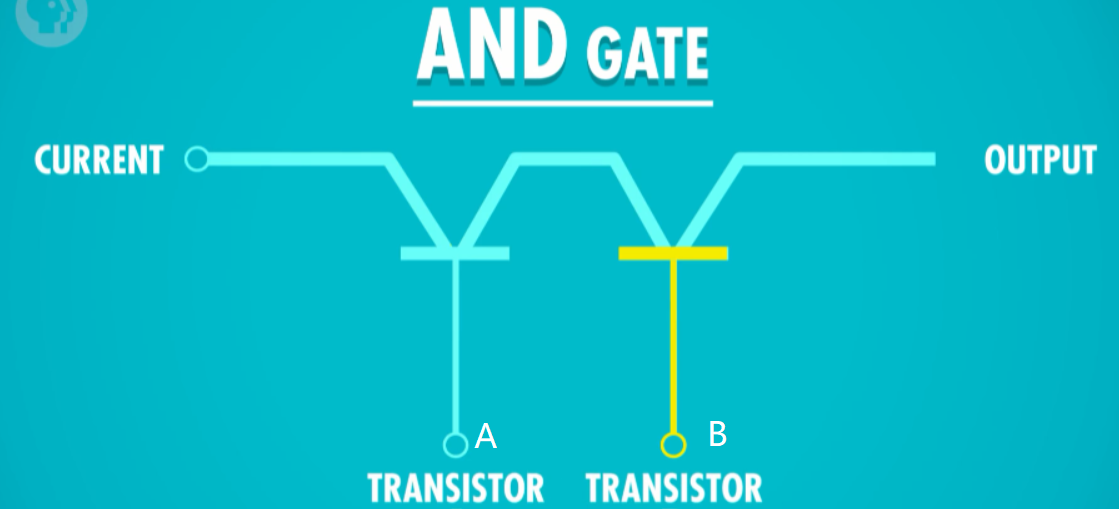
如果只打开 A,不打开 B N 电流无法流到 output,所以输出是 false,如果只打开 B,不打开 A ,也一样,电流无法流到 output,只有 A 和 B 都打开了,output 才有电流。
5、OR
最后一个是 OR (前面讲了 NOT 和 AND),只要 2 个输入里,其中 1 个是 true,输出就是 true。
| INPUT A | INPUT B | OUTPUT |
| TRUE | TRUE | TRUE |
| TRUE | FALSE | TRUE |
| FALSE | TRUE | TRUE |
| FALSE | FALSE | FALSE |
比如,我叫 Margaret Hamilton"或"我穿着蓝色衣服,结果是 true,虽然我不是 Margaret Hamilton,但是我穿着蓝色衣服,所以结果是 true。
对于"OR 操作"来说,N如果 2 个 输入都是 true,输出也是 true,只有 2 个输入都是 false,OR 的结果才是 false。
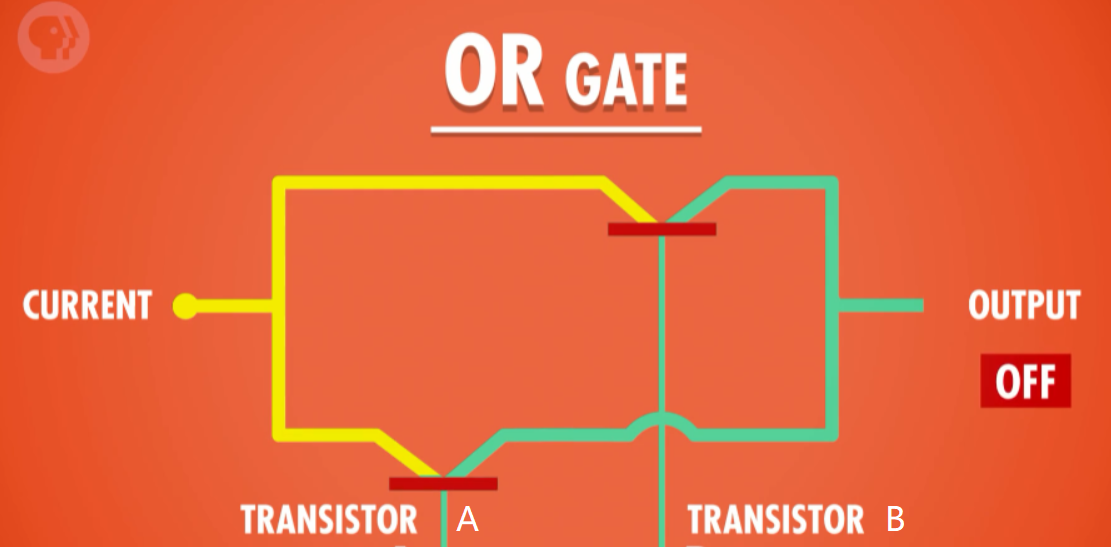
实现 "OR 门" 除了晶体管还要额外的线,不是串联起来,而是并联。然后左边这条线有电流输入

我们用"小拱门"代表 2 条线没连在一起,只是跨过而已,虽然看起来像连在一起,如果 A 和 B 都是 off,电流无法流过,所以输出是 off;如果打开 A,电流可以流过。输出是 on,如果只打开 B 也一样,只要 A OR B 是 on, 输出就是 on,如果 A 和 B 都 on,结果是 on。
好,现在 NOT 门, AND 门, OR 门 都搞定了。我们可以进行一次抽象,NOT 门的画法是三角形前面一个圆点,
AND 门用 D 表示 ,
OR 门用太空船表示,

"D 形状和太空船"不是标准叫法, 只是我喜欢这样叫而已。我们可以用这种方法表示它们,构建更大的组件,就不会变得很复杂——晶体管和电线依然在那里,我们只是用符号来代表而已。
6、XOR
除了前面说的三个N 另一个有用的布尔操作叫 "异或"——简称 XOR。
| INPUT A | INPUT B | OUTPUT |
| TRUE | TRUE | FALSE |
| TRUE | FALSE | TRUE |
| FALSE | TRUE | TRUE |
| FALSE | FALSE | FALSE |
XOR 就像普通 OR,但有一个区别:如果 2 个输入都是 true,XOR 输出 false。想要 XOR 输出 true N 一个输入必须是 true,另一个必须是 false,就像你出去吃晚饭,你点的饭要么配沙拉,要么配汤——你不能两个都要!
用晶体管实现 XOR 门有点烧脑子,但我可以展示一下N 怎么用前面提到的 3 种门来做 XOR 门。

我们有 2 个输入,A 和 B ,还有 1 个输出.,我们先放一个 OR 门. 因为 OR 和 XOR 的逻辑表很像,只有 1 个问题 - 当 A 和 B 都是 true 时 N OR 的输出和想要的 XOR 输出不一样,我们想要 false。XOR 超有用的,我们下次再说它。因为超有用,N 工程师给了它一个符号,一个 OR 门 + 一个笑脸,重要的是,现在可以把 XOR 放入"工具箱"了,不用担心 XOR 具体用了几个门,这几个门又是怎么用晶体管拼的,或电子是怎么流过半导体的,再次向上抽象。
工程师设计处理器时,很少在晶体管的层面上思考,而是用更大的组件,比如逻辑门,或者由逻辑门组成的更大组件,我们以后会讲。就算是专业程序员,也不用考虑逻辑是怎样在物理层面实现的。
我们从电信号开始,到现在第一次表示数据——真和假 - 开始有点"计算"的感觉了。仅用这一讲讲的 逻辑门,我们可以判断复杂的语句 比如:[如果是 John Green] AND [下午 5 点后] N OR [周末] AND [在比萨店附近]。那么 "John 想要比萨" = 真
最后
以上就是爱笑项链最近收集整理的关于计算机科学第三讲——布尔逻辑和逻辑门的全部内容,更多相关计算机科学第三讲——布尔逻辑和逻辑门内容请搜索靠谱客的其他文章。
![[2018.03.29 T1] 异或](https://file2.kaopuke.com:8081/files_image/reation/bcimg12.png)







发表评论 取消回复