运动规划学习笔记（持续更新中）

1.Mathematically, the motion planning problem is a high-dimensional non-convex optimization problem that is subject to static and dynamic obstacle constraints, kinematic constraints (e.g. curvature bounds), dynamic constraints (e.g. speed limit, acceleration limit, jerk limit), a nonlinear time-varying dynamic system model, traffic rules, smoothness requirements, and most importantly realtime requirements.

2.Wenda Xu在其博士论文Motion Planning for Autonomous Vehicles in Urban Scenarios: A Sequential Optimization Approach中的规划框架：

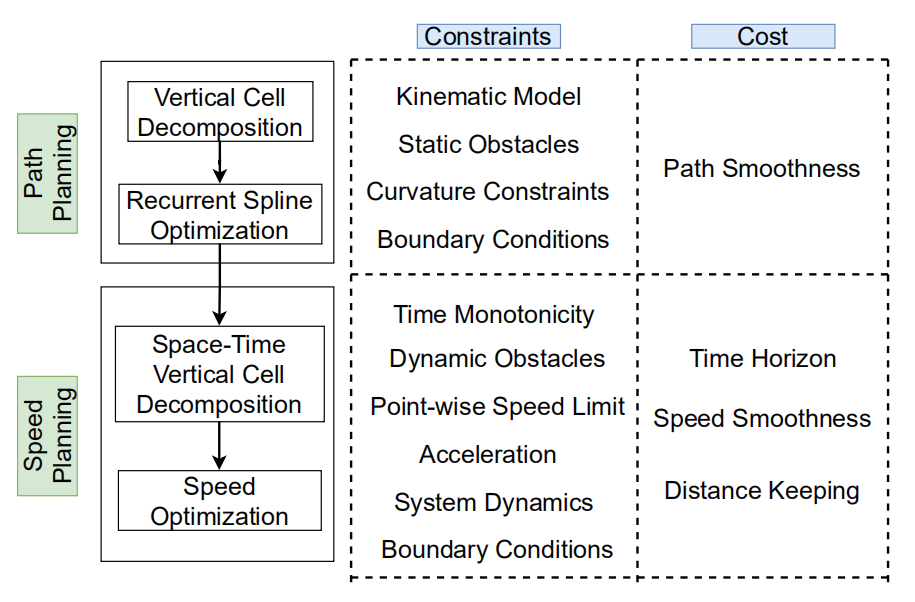
First, we use a vertical cell decomposition method to handle static obstacles,where the free-space is partitioned into a set of cells. Each cell is either a trapezoid or a triangle. The corridor is built by a list of connected convex cells.

Second, given the path corridor, a convex path optimization is applied to obtain a collision-free smooth path that also obeys the kinematic model. Based on Differential Flatness theory, the path optimization is formulated as a constrained convex optimization problem, which guarantees a global optimum. The curvature constraints are handled by an iterative optimization approach.

Third, we propose a space-time vertical cell decomposition method to handle dynamic obstacles. Compared to the normal vertical cell decomposition method, additional constraints need to be considered. Any feasible solution should be no faster than the minimum-time solution. Moreover, time should be monotonically increasing.

Fourth, given the coarse collision-free speed profile and the S-T corridor, a novel speed optimizer is proposed. Compared to previous methods, it can handle constraints on the station dimension such as velocity limit and stop line and constraints on the time dimension such as moving obstacles simultaneously based on iterative quadratic programming (QP). It can handle cases such as yielding to other traffic as well as merging in front of other vehicles.

3.轨迹生成的两种方法
There are two types of trajectory generation methods: forward kinematics and inverse kinematics. In forward kinematics, the initial state of the robot and control input are given, and the final state can be obtained through integrating the control input. Typical numerical integration methods include the Euler, Simpson, and Runge-Kutta methods. In inverse kinematics, the initial and final state of the robot are given, and the control input is to be determined. It usually requires solving a system of algebraic equations if the trajectory can be represented by polynomials or a trajectory optimization problem for general nonlinear systems.

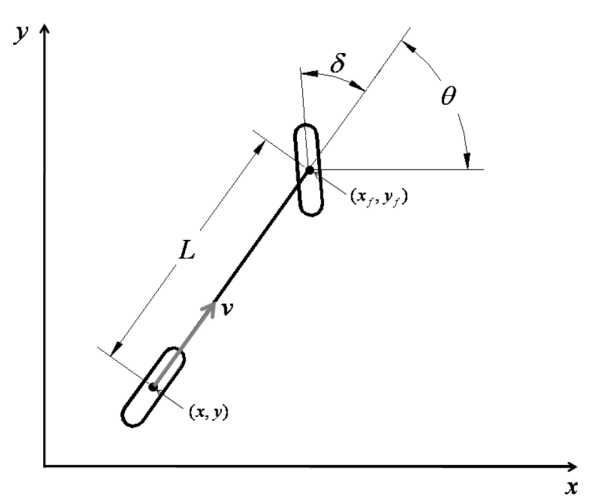
4.运动学自行车模型

5.微分平坦性
微分平坦的定义：

车辆的状态（x,y,θ,δ）都可以用x和y相关的量来表示：


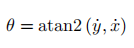
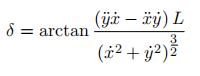
控制量(v,ω)也可以用x和y相关的量来表示：


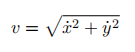
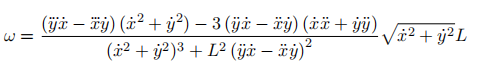
由此可见，如果车辆轨迹是三阶可导的，那自然就满足非完整性的运动学约束。

6.关于曲率

最后

以上就是感动早晨为你收集整理的运动规划学习笔记（持续更新中）的全部内容，希望文章能够帮你解决运动规划学习笔记（持续更新中）所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。