判定表与判定树的画法_NP完全性理论--判定问题、NP类、多项式时间变换、处理NP难问题的策略、0-1背包的近似解学习笔记...

PS1:先安利一个科普视频给各位压压惊P=NP是啥？玩数独就可以得100万，你信吗？看完就懂了！
PS2：幽你一默--我发现了NPC的绝妙算法，可惜知乎的评论框太小，写不下。呜呜呜

NP完全性理论大纲

易解的问题与难解的问题
判定问题
NP类
多项式时间变换
NP完全性及其性质
处理NP难问题的策略

易解的问题与难解的问题

好算法的标准

输入规模和算法运行时间

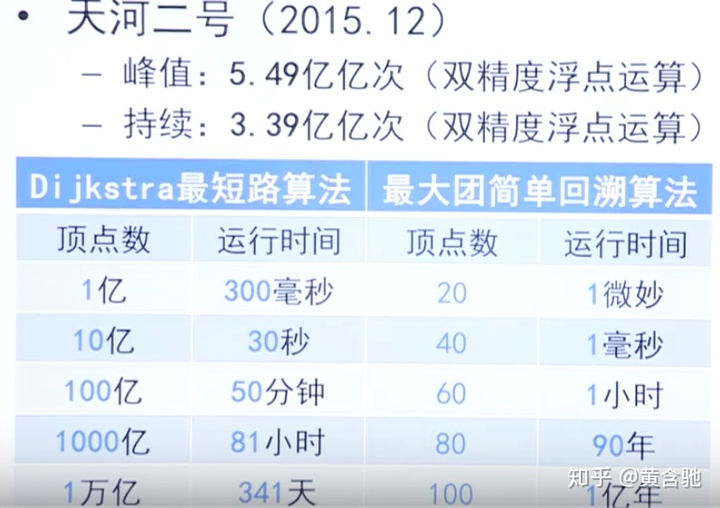
问题的难与易

多项式相关的概念

图的2种编码方式--邻接矩阵、关联矩阵

问题实例的合理编码

算法运行时间是基本操作数

问题难易与编码和指令集的选择无关

易解问题和难解问题

什么是P和NP问题

什么是多项式时间可验证

NP-非确定性多项式时间算法

哈密尔顿回路的NP算法

0-1背包问题

所有P都是NP

多项式时间变换

如何比较2问题难度

什么是多项式时间变换

最大生成树和最小生成树

的性质——传递性

能多项式时间变换到P类问题都是P类问题

难解问题能多项式时间变换到的都是难解问题

NP难和NP完全（NPC）

对任意NP问题，它都不比问题

更难，所以

叫做NP难。

NPC中最典型的就是售货员旅行问题。其他如数独、扫雷、俄罗斯方块也可以变成NPC问题。就目前来说，人类还没有发现任何NPC问题更优越的算法能够变成P类问题。
PS:此处安利一个科普视频P=NP是啥？玩数独就可以得100万，你信吗？看完就懂了！

关于P和NP

所以只要发现一个NP难问题存在多项式时间算法，我们就可以证明P=NP

P和NP的可能的四种关系（至于哪种关系正确，这还有待后人研究）

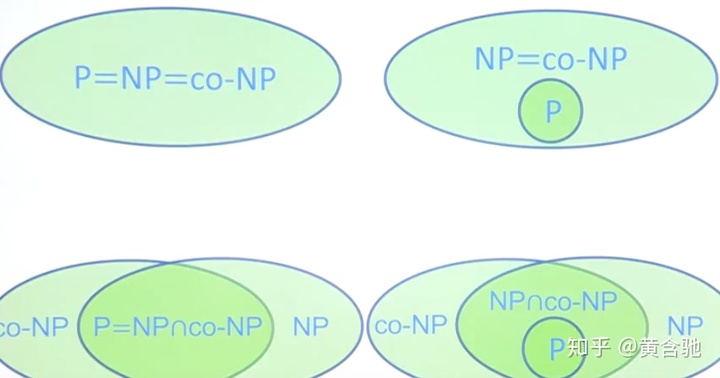
什么是co-NP:
栗子--判定一个图是否有哈密尔顿回路--NP问题；判定一个图是否 无哈密尔顿回路--co-NP问题

如何证明问题是NP完全的

Cook Levin定理——第一个NP完全问题

可惜它讲解起来比较繁琐，有兴趣的童鞋可以康康视频https://www.youtube.com/watch?v=mAALkpRWhG8&list=PLEbxAdiNxjMYlNgstf8aHDf-o0E31ujmU&index=46~

处理NP难问题的策略

对问题施加限制如限制参数长度
改进指数时间算法
启发式方法
平均情形的复杂性
难解算例的生成——通过难解算例来做对算法的评价标准

对问题施加限制

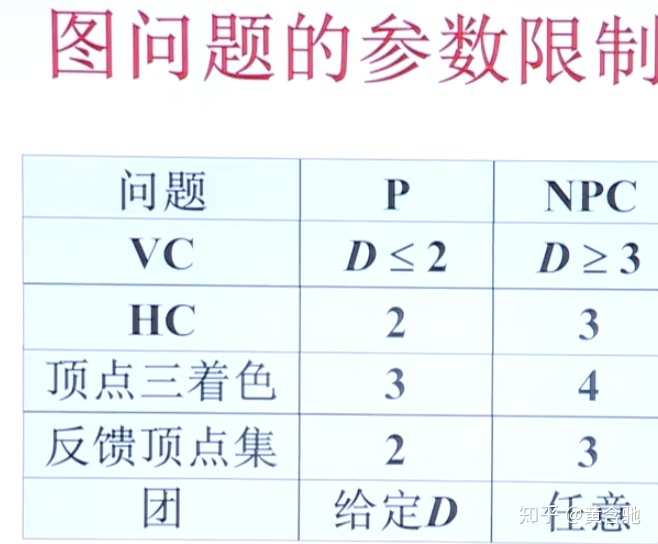
固定参数算法

顶点覆盖问题VC

改进指数时间算法

SAT问题及其他问题的有关结果

启发式算法

局部搜索算法

平均情况的复杂度

难解算例的生成

小结

案例分析：0-1背包的近似解

问题描述

贪心算法G-KK

贪心算法G-KK的性能--2-近似算法

多项式时间近似方案PTAS

实例 n=10

=0.2 m=5

PTAS性能

时间复杂度

小结

参考资料：（视频）https://www.youtube.com/watch?v=ANJWc-CJN_Q&list=PLEbxAdiNxjMYlNgstf8aHDf-o0E31ujmU&index=40https://www.youtube.com/watch?v=rNw34dQPoYchttps://www.youtube.com/watch?v=xmkuiSAKlXQhttps://www.youtube.com/watch?v=idpooA8v0sg&t=15shttps://www.youtube.com/watch?v=mAALkpRWhG8&list=PLEbxAdiNxjMYlNgstf8aHDf-o0E31ujmU&index=46https://www.youtube.com/watch?v=wS3ix6h-bxw&t=1s