一招团灭动态规划（附所有DP问题汇总）（新手向）前言动态规划的理解动态规划的思维模式后记附文

60 阅读 0 评论 40 点赞

我是靠谱客的博主傻傻樱桃，最近开发中收集的这篇文章主要介绍一招团灭动态规划（附所有DP问题汇总）（新手向）前言动态规划的理解动态规划的思维模式后记附文，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

点赞再看，养成习惯，您动动手指对原创作者意义非凡????
备战2021秋招面试微信搜索公众号【TechGuide】关注更多新鲜好文和互联网大厂的笔经面经。
作者@TechGuide

前言

碰到太多的人面试倒在动态规划上了，惋惜之后，毅然写下此文并附上所有的DP问题（和链接）供大家练习用。看完这篇文章，你会发现其实动态规划并没有想象的那么难，不要被它高大上的名字给唬住。只要你够有决心，就算你是新手，动态规划也可以一口气整个给它盘下来。(当然大神都是不用套路，无师自通的，请四十五度角仰望天空保持高冷)
在这里插入图片描述

动态规划的理解

开篇第一问，动态规划是什么？动态体现在哪里？又规划了什么？~~（欸，不对，好像是三问了）~~

开篇第一答，动态规划问题其实就是 $“ 递归 + 记忆化 ”$ ，这里还不明白这句话没有关系，但是要记着这句话和上面提出的三个问题看下去。

在这里插入图片描述
递归我们再熟悉不过了，自己反复调用自己嘛，俗称套娃。比如已经被用烂了但我这里还要再用一次的经典用例——斐波那契数列。防止部分新手没有听过这个数列，我给出其定义：

即定义这样一个数列，前两项值等于序列号，后面每一项是前两项之和，这样就可以通过反复调用自身来求解每一项的值，可以用这样的程序实现：

int Fib(int n)
{
	return n < 2 ? 1 : (Fib(n-1) + Fib(n-2));
}

有人第一次看到这样的递归程序的时候，会觉得这样通过调用函数本身从而避免了冗长繁琐的代码，减轻了程序员繁重的代码量，是一种使用的好方法。
在这里插入图片描述
实际情况是，当n=40时，这段程序在我的8G内存i5 8代的笔记本上运行时间如下：

惊不惊喜？意不意外？

造成运行时间爆炸的原因很简单，我们只是单纯的用了递归，所以求解每一项，我们都要重新计算之前的每一项，层层套娃就算了，还反复套，这能不费劲吗？就比如我们求解fib（6）的时候，又得重复计算fib(5)和fib（4），但是这两项我们之前就已经计算过了，所以这里有大量的重复计算，复杂度可以达到O（2ⁿ），所以得到上面的运行时间也就不意外了。
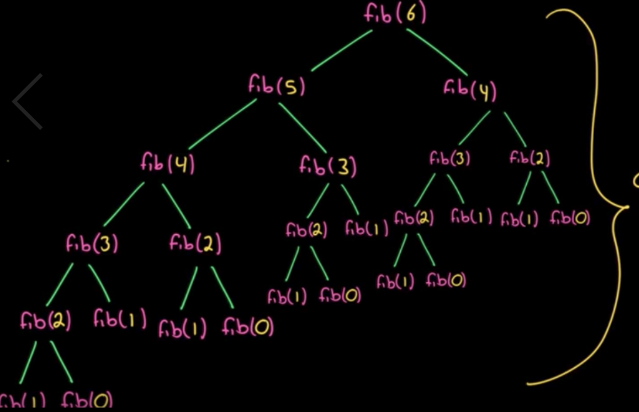
在这里插入图片描述
那就有聪明的小伙伴问啦，有没有解决的办法呢？有！记忆化！记住之前求的每一项不就得了，没计算出一项我就把这个值保存下来，这样我后面需要再用到的时候可以直接用，复杂度变成O(n)，上面的程序也可以改进成下面这个程序：

int Fibonacci(int n)
{
    if(n==1||n==2)
        return 1;
    else if(n<=0)
        return 0;
    else if(!memo[n])  //如果没有计算过，就计算一次并存下来
   		memo[n]=Fibonacci(n-1)+Fibonacci(n-2);
    return memo[n];  //如果计算过了，直接返回之前记忆的计算结果
}

动态规划的思维模式

实际以上例子就是一个经典的动态规划问题，我们可以回顾下文章开始说的递归+记忆化，我们如果能够记住我们之前每次运行的结果，那么就可以从第一项一直递推到最后一项，求解出我们需要的结果，如果我们把这其中每一项称为一个状态，比如这里的fib(0),fib(1),fib(2),fib(3)…，那么我们我们想求解的任一目标值实际也就是一个状态，比如这里的fib(6)，我们要做的就是把前面已知的状态递推到待求的目标状态上，所以动态就是它是有很多状态的，我们需要在这些状态间转移，规划出最优解（状态）的路线。这就需要一个状态转移方程，比如Fib(n) = Fib(n-1) + Fib(n-2)就是从前面的状态转移到现状态的转移方程（方式）。
总结一下：

状态定义（建数组）
状态转移方程（数组存值）

讲了动态规划的最简单的一个例子，接下来咱来个最难的一道，股票买卖问题IV，直接用以上套路。

给定一个数组，它的第 i 个元素是一支给定的股票在第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你最多可以完成 2笔交易（买一次再卖一次）。

示例 1:

输入: [2,4,1]
输出: 2
解释: 在第 1 天 (股票价格 = 2) 的时候买入，在第 2 天 (股票价格 = 4) 的时候卖出，这笔交易所能获得利润 = 4-2 = 2 。
<题目链接>

怎么解这道问题呢？第一步，状态的定义。
怎么定出一道动态规划题目的状态呢？这里有一个技巧，根据求解的目标状态来定义，比如这里我们要计算第i天最多k笔交易的情况下的最大利润。（要涵盖住所有变量）。前面斐波那契数列的状态很好保存，就是第n项的值嘛，直接一维数组DP[]妥妥摆平·，但是这里有两个变量分别是交易数，和天数，怎么办呢？用二维数组保存吧，这样我就可以一个状态和两个参数相关联了，美汁汁。

在这里插入图片描述
给出我们的状态（定义数组）如下：

DP[k][i] //第i天最多j笔交易的情况下的最大利润

如此，我们就可以依据显而易见的初始状态一步一步往后递推到目标状态。比如DP[0][0]=0表示：k 是从 1 开始的，所以 k = 0 意味着根本不允许交易，这时候利润当然是 0 。怎么递推呢？没错，第二步，状态转移方程！

一说到状态转移，立马就有点头晕了，实际上我们可以从最简单的状态开始，怎么从第0天的状态转移到第1天呢？这就要分情况，第1天可能买股票，啥也不干或者卖股票，我们就分别针对这些情况定义出其状态转移方程即可（所以越复杂的动态规划问题无非就是多几个参数的数组定义和多几条状态转移方程。）

DP[k][i] = max(DP[k][i-1], DP[k-1][i-1] + prices[i])

解释：今天最大利润的状态是DP[k][i]，有两种可能：
要么是我昨天就除天数外一模一样的状态DP[k][i-1]，今天啥也不干；
要么是我昨天最大利润的状态是DP[k-1][i-1]，但是今天我卖了一支股票，所以我获得 prices[i]的利润。

上面是这个思路很好，但是有一个问题，我第i天可以卖的前提是我之前买了，所以这里我是假设我卖之前都买过一次的，那么问题就来了(不要问为什么这么多问题，不然怎么好意思吹嘘自己是最难的一道DP问题)，怎么确定哪一天买进了一只股票呢？我们就得找出在第i天判断之前i-1天内哪一天买才能得到最大利润！，得到下面的状态转移方程。

DP[k][i] = Math.max(DP[k][i - 1], prices[i] + tmpMax);
tmpMax = Math.max(tmpMax, DP[k-1][i-1] - prices[i]);

解释：今天最大利润的状态是DP[k][i]，有两种可能：
要么是我昨天就除天数外一模一样的状态DP[k][i-1]，今天啥也不干；
要么是我昨天或者之前哪一天最大利润的状态是DP[k-1][i-1]，然后今天我卖了一支股票，所以我获得 prices[i]的利润。

这样我们就得到下面的程序，如果想弄透的话，现在看了不明白的可以收藏，再多做几道较简单的DP问题练手（附文里有汇总），也可以多看几遍，多理解理解，然后自己在实际运行一下，建议debug。实在不明白的可以评论交流。

public int maxProfitIII(int[] prices, int times){ //{7,1,5,3,6,4}
        int[][] DP = new int[times+1][prices.length];  //
        for (int k = 1; k < times+1; i++) {
            int tmpMax = -prices[0];  //初始记录如果这时候购买有多少利润，虽然血亏，最好还是记录一下，后面会被替换掉。
            for (int i = 1; i < prices.length; i++) {
                    DP[k][i] = Math.max(DP[k][i - 1], prices[i] + tmpMax);
                    tmpMax =  Math.max(tmpMax, DP[k-1][i-1] - prices[i]); //找到最大利润购买时机
                }
            }
        return DP[times][prices.length-1]; //返回最后一个状态
    }

后记

费尽心力写了这么多，这里还想最后再啰嗦几句，动态规划要学吗？要学，程序员只有过了面试才能维持得了生活这样子。动态规划好用吗？实际工作基本用不上。它就像你摆在家里客厅的一只花瓶，时刻彰显主人家的高贵气质和艺术修养，但是你指望一只花瓶帮你盛菜煲汤，填饱肚子，那就有点强瓶所难了，所以我更愿意相信，学习动态规划，也只是锻炼你的思维能力和编程能力，仅此而已。

附文

DP问题总览图

在这里插入图片描述

附力扣链接

（整理不易，点个赞吧~）

不同的二叉搜索树 (卡特兰数)
N 天后的牢房
骑士拨号器
最大为 N 的数字组合
鸡蛋掉落 (DP+二分)
石子游戏
新21点
分汤
有效的井字游戏
统计不同回文子字符串
编辑距离
买卖股票的最佳时机含手续费
爬楼梯
奇怪的打印机
不同路径 II
不同路径
出界的路径数
二叉树的直径
最大子序和
优美的排列
零钱兑换 II (完全背包-求方案数)
最长回文子序列
斐波那契数
目标和 (01背包-求方案数)
一和零 (二维费用背包)
我能赢吗
通配符匹配
分割等和子集 (01背包-要求恰好取到背包容量)
俄罗斯套娃信封问题 (隐晦的LIS)
判定井字棋胜负
打家劫舍 III
最大 BST 子树
矩阵中的最长递增路径
零钱兑换 (完全背包)
戳气球
最佳买卖股票时机含冷冻期
最长上升子序列 (LIS)
翻转游戏 II
翻转游戏
Nim 游戏
数字 1 的个数
打家劫舍 II
打家劫舍
买卖股票的最佳时机 IV
乘积最大子数组
参加考试的最大学生数
找出井字棋的获胜者
不相交的握手 (卢卡斯定理求大组合数模质数)
树的直径 (邻接表上的树形DP)
二叉树中的最大路径和
买卖股票的最佳时机 III
买卖股票的最佳时机 II
买卖股票的最佳时机
三角形最小路径和
石子游戏 II
第 N 个泰波那契数
多边形三角剖分的最低得分
可被 K 整除的最小整数
正则表达式匹配