【算法题解–序列DP】Leetcode10. 正则表达式匹配

一、题目描述

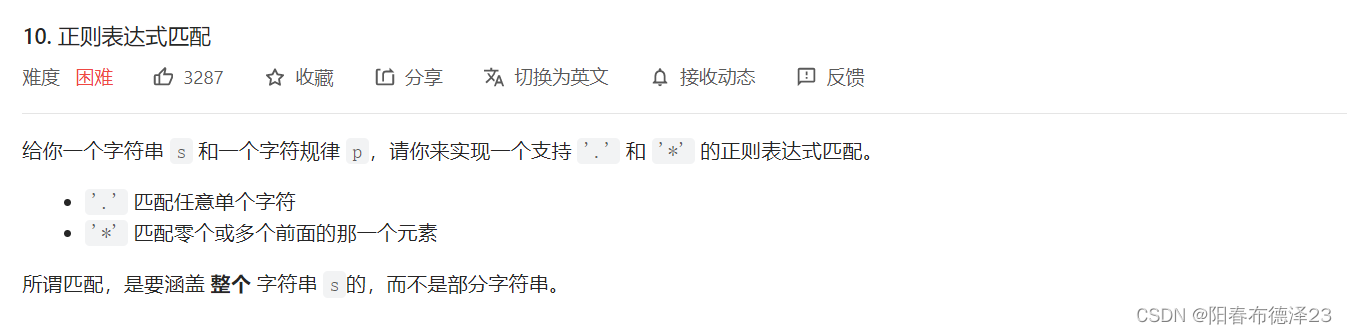
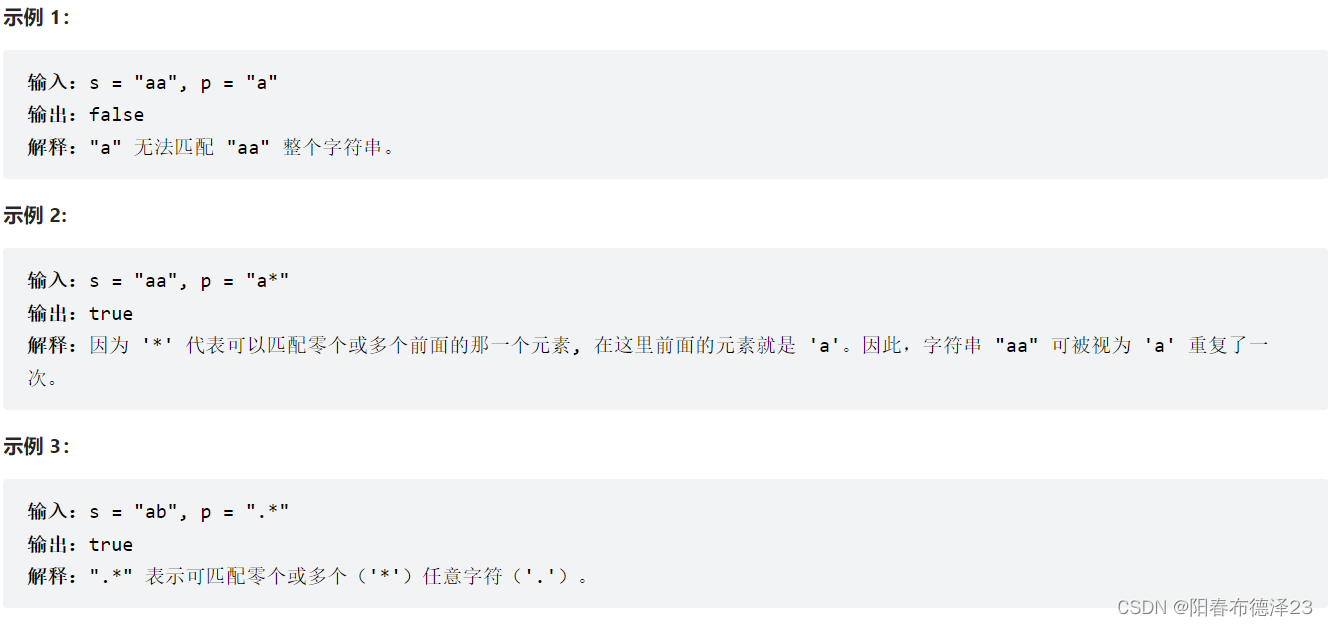
二、解决方案

1.思路分析

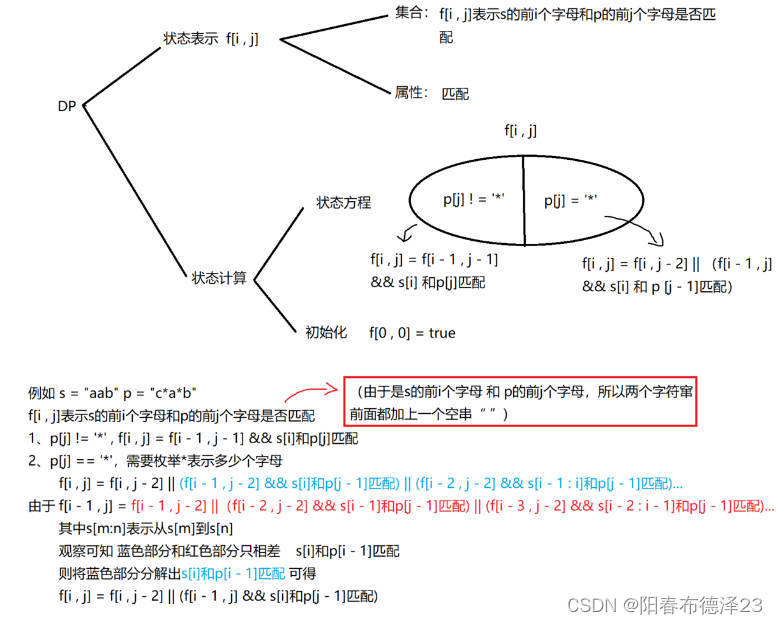
• 根据题目描述，可以使用动态规划方法——二维DP（两个字符串）
• f[i,j]为bool类型，表示s串的前i个字符和p串的前j个字符是否匹配
• 递推公式化简与完全背包问题类似

时间复杂度：O(mn)
空间复杂度：O(mn)

2.代码展示

代码如下（示例）：

class Solution {
public:
    bool isMatch(string s, string p) {
       int m = s.size(), n = p.size();
       s = ' '+s;
       p = ' '+p;
       vector<vector<bool> > dp(m+1,vector<bool>(n+1,false));
       dp[0][0] = true;
       for(int i=0;i<=m;i++){
           //s串为空的时候也有可能匹配成功（eg.p="a*"），所以i从0开始遍历
           for(int j=1;j<=n;j++){ 
               //p串为空的时候一定不能匹配，默认为false，所以j从1开始就可以
                if(j+1<=n && p[j+1]=='*') continue;
                if(i>=1 && p[j]!='*'){ //注意i的判断防止越界
                    dp[i][j] = dp[i-1][j-1] && (s[i]==p[j] || p[j]=='.');
                }
                else if(p[j]=='*'){
                    dp[i][j] = dp[i][j-2]||(i>=1 && dp[i-1][j] && (s[i]==p[j-1] || p[j-1]=='.')); //注意i的判断防止越界
                }
           }
       }
       return dp[m][n];
    }
}; 

链接: 力扣题解

最后

以上就是秀丽饼干为你收集整理的【算法题解--动态规划】Leetcode10. 正则表达式匹配【算法题解–序列DP】Leetcode10. 正则表达式匹配一、题目描述二、解决方案的全部内容，希望文章能够帮你解决【算法题解--动态规划】Leetcode10. 正则表达式匹配【算法题解–序列DP】Leetcode10. 正则表达式匹配一、题目描述二、解决方案所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。