You have a map as a rectangle table. Each cell of the table is either an obstacle, or a treasure with a certain price, or a bomb, or an empty cell. Your initial position is also given to you.
You can go from one cell of the map to a side-adjacent one. At that, you are not allowed to go beyond the borders of the map, enter the cells with treasures, obstacles and bombs. To pick the treasures, you need to build a closed path (starting and ending in the starting cell). The closed path mustn't contain any cells with bombs inside. Let's assume that the sum of the treasures' values that are located inside the closed path equals v, and besides, you've made k single moves (from one cell to another) while you were going through the path, then such path brings you the profit of v - k rubles.
Your task is to build a closed path that doesn't contain any bombs and brings maximum profit.
Note that the path can have self-intersections. In order to determine if a cell lies inside a path or not, use the following algorithm:
- Assume that the table cells are points on the plane (the table cell on the intersection of the i-th column and the j-th row is point(i, j)). And the given path is a closed polyline that goes through these points.
- You need to find out if the point p of the table that is not crossed by the polyline lies inside the polyline.
- Let's draw a ray that starts from point p and does not intersect other points of the table (such ray must exist).
- Let's count the number of segments of the polyline that intersect the painted ray. If this number is odd, we assume that point p (and consequently, the table cell) lie inside the polyline (path). Otherwise, we assume that it lies outside.
The first line contains two integers n and m (1 ≤ n, m ≤ 20) — the sizes of the table. Next n lines each contains m characters — the description of the table. The description means the following:
- character "B" is a cell with a bomb;
- character "S" is the starting cell, you can assume that it's empty;
- digit c (1-8) is treasure with index c;
- character "." is an empty cell;
- character "#" is an obstacle.
Assume that the map has t treasures. Next t lines contain the prices of the treasures. The i-th line contains the price of the treasure with index i, vi ( - 200 ≤ vi ≤ 200). It is guaranteed that the treasures are numbered from 1 to t. It is guaranteed that the map has not more than 8 objects in total. Objects are bombs and treasures. It is guaranteed that the map has exactly one character "S".
Print a single integer — the maximum possible profit you can get.
1
2
3
4
5
64 4 .... .S1. .... .... 10
12
1
2
3
4
5
6
7
8
9
10
11
127 7 ....... .1###2. .#...#. .#.B.#. .3...4. ..##... ......S 100 100 100 100
1364
1
2
3
4
5
6
7
8
9
10
117 8 ........ ........ ....1B.. .S...... ....2... 3....... ........ 100 -100 100
10
1
21 1 S
10
In the first example the answer will look as follows.
In the second example the answer will look as follows.
In the third example you cannot get profit.
In the fourth example you cannot get profit as you cannot construct a closed path with more than one cell.
题意：
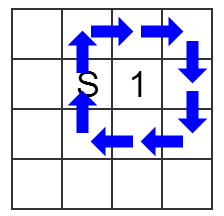
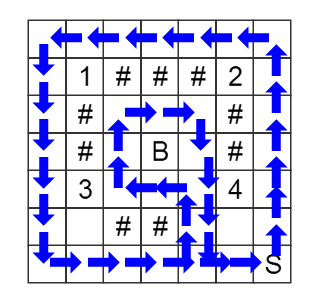
给你一个地图，上面有一些宝石、炸弹，让你从一个点出发回到这个点，使圈起来的宝石的价值-步数最大，并且不能圈到炸弹，能够圈到‘#’，一个点允许重复走。
思路：
就是 poj3182 的加强版，建议先做这个题，可以参考：poj 3182 题解
预处理每个圈住宝石的状态的价值，炸弹可当做价值为负无穷的宝石，取dp[x][y][k]判重，x、y为位置，k为圈住宝石的状态，剩下的就是怎样判断一个路径圈住宝石的状态了，方法是过点做一条射线，这个射线与多边形交奇数次为在多边形内，偶数次则为多边形外，具体操作只需要虚拟的射线就够了。
代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158#include <iostream> #include <cstdio> #include <cstring> #include <algorithm> #include <cmath> #include <string> #include <map> #include <stack> #include <vector> #include <set> #include <queue> //#pragma comment (linker,"/STACK:102400000,102400000") #define maxn 25 #define mod 1000000007 #define INF 0x3f3f3f3f #define OO 0xbfbfbfbf using namespace std; typedef long long ll; int n,m,ans,cnt,flag,tot; int sx,sy; int dx[]= {-1,1,0,0}; int dy[]= {0,0,-1,1}; int dp[maxn][maxn][1<<8]; int val[8],w[1<<8]; int gx[8],gy[8]; char mp[maxn][maxn]; char s[maxn]; struct Node { int x,y,k; } cur,now; bool issur(int nx,int ny,int tx,int ty,int j) { if(nx==gx[j]&&ny<gy[j]) { if(tx<gx[j]) return true ; } else if(tx==gx[j]&&ty<gy[j]) { if(nx<gx[j]) return true ; } return false ; } void bfs() { int i,j,t,k,nx,ny,tx,ty,nk; queue<Node>q; memset(dp,-1,sizeof(dp)); ans=-INF; cur.x=sx; cur.y=sy; cur.k=0; dp[sx][sy][0]=0; q.push(cur); while(!q.empty()) { now=q.front(); q.pop(); nx=now.x; ny=now.y; nk=now.k; if(nx==sx&&ny==sy) ans=max(ans,w[nk]-dp[nx][ny][nk]); for(i=0; i<4; i++) { tx=nx+dx[i]; ty=ny+dy[i]; k=nk; if(tx<1||tx>n||ty<1||ty>m) continue ; if(!(mp[tx][ty]=='S'||mp[tx][ty]=='.')) continue ; for(j=0;j<=cnt;j++) { if(issur(nx,ny,tx,ty,j)) k^=(1<<j); } if(dp[tx][ty][k]!=-1&&dp[tx][ty][k]<=dp[nx][ny][nk]+1) continue ; cur.x=tx; cur.y=ty; cur.k=k; dp[tx][ty][k]=dp[nx][ny][nk]+1; q.push(cur); } } } int main() { int i,j,t; while(~scanf("%d%d",&n,&m)) { cnt=-1; for(i=1; i<=n; i++) { scanf("%s",s); for(j=1; j<=m; j++) { mp[i][j]=s[j-1]; if(mp[i][j]=='S') sx=i,sy=j; if(mp[i][j]>='1'&&mp[i][j]<='8') { t=mp[i][j]-'1'; cnt++; gx[t]=i,gy[t]=j; } } } for(i=0;i<=cnt;i++) { scanf("%d",&val[i]); } for(i=1; i<=n; i++) { for(j=1; j<=m; j++) { if(mp[i][j]=='B') gx[++cnt]=i,gy[cnt]=j,val[cnt]=-10000; } } memset(w,0,sizeof(w)); tot=1<<(cnt+1); for(i=0;i<tot;i++) { for(j=0;j<=cnt;j++) { if(i&(1<<j)) w[i]+=val[j]; } } bfs(); printf("%dn",ans); } return 0; } /* 3 3 ... SB. ... 10 11 ........S.. ........... 5........1. .7#........ ...64.#.... ........... ..........# .2......... .....3..... ........... -9 33 9 -20 12 10 -29 ans:0 8 */
最后
以上就是能干酸奶最近收集整理的关于Codeforces Round #221 (Div. 2) E. Circling Round Treasures （搜索+判断点在多边形内）的全部内容，更多相关Codeforces内容请搜索靠谱客的其他文章。
发表评论 取消回复