栈和队列实验目的栈队列

65 阅读 0 评论 43 点赞

我是靠谱客的博主自信黄蜂，最近开发中收集的这篇文章主要介绍栈和队列实验目的栈队列，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

本文章为考试复习向，偏基础，用来复习仅供参考。
本文章内容基于众多优秀博客所整理的笔记，所参考的博客都会在本文最后列出。

数据结构学习——栈与队列

实验目的
栈
- 栈的介绍
- 顺序栈
- 链栈
队列
- 队列介绍
- 顺序队列
- 顺序循环队列
- 链式队列

实验目的

1、掌握栈和队列的概念和存储表示。

2、掌握栈和队列的基本功能的实现。

栈

栈的介绍

栈是一个先入后出的有序列表。
栈(stack)是限制线性表中元素的插入和删除只能在线性表的同一端进行的一种特殊线性表。允许插入和删除的一端，为变化的一端，称为栈顶(Top)，另一端为固定的一端，称为栈底(Bottom)。
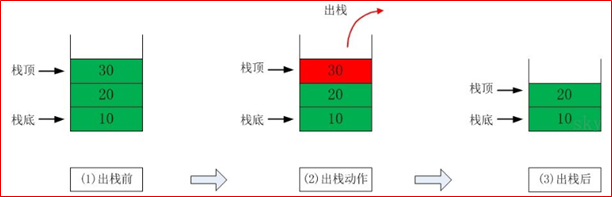
根据栈的定义可知，最先放入栈中元素在栈底，最后放入的元素在栈顶，而删除元素刚好相反，最后放入的元素最先删除，最先放入的元素最后删除。
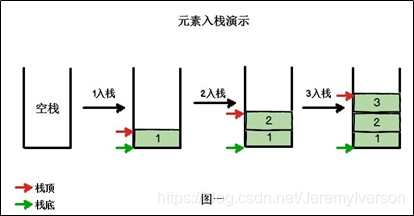
图解方式说明出栈(pop)和入栈(push)的概念:
栈（stack）是一种先进后出的线性结构。只允许在栈的一端进行插入和删除操作，称为栈顶（top），栈的另一端称为栈底（Bottom）。栈顶的当前位置是动态变化的，由栈顶指针的位置指示，栈底指向栈的末尾。

顺序栈

1)顺序栈的基本特性及概念
顺序栈使用顺序表(数组)实现。顺序栈的示意图如下：

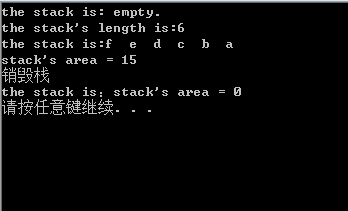
在这里插入图片描述

2)顺序栈对顶栈的基本操作及实现(初始化、出入栈、栈是否为空、获取栈顶元素、弹出栈顶元素、求栈内元素个数)
代码如下：

#include <stdio.h>
#include <assert.h>
#include <stdlib.h>
#include <stdlib.h>
#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0
#define OVERFLOW -1
#define SS 5
#define Increment 10

typedef int Status;
typedef char SElemType;
typedef struct{
	SElemType *base, *top;
	int stacksize;
} SqStack;

//初始化
Status InitStack(SqStack &S)
{
	S.base = (SElemType*)malloc(sizeof(SElemType) * SS);
	if(! S.base)
		exit(OVERFLOW);
	S.top = S.base;
	S.stacksize = SS;
	return OK;
} 

//求长度
int StackLength(SqStack S)
{
	return S.top - S.base;
} 

//摧毁栈 
Status DestroyStack(SqStack &S)
{
	S.top = S.base;
	free(S.base);
	S.base = NULL;
	S.top = NULL;
	S.stacksize = 0;
	return OK; 
}

//判断栈是否为空
Status StackEmpty(SqStack S)
{
	if(S.top == S.base)
		return OK;
	else return ERROR;
} 

//取栈顶元素
Status GetTop(SqStack S, SElemType &e)
{
	if(S.top == S.base )
		return ERROR;
	e = *(S.top - 1);
	return OK;
} 

//入栈
Status Push(SqStack &S, SElemType e)
{
	if(S.top - S.base >= S.stacksize )
	{
		S.base = (SElemType*)realloc(S.base,(S.stacksize + SS) * sizeof(SElemType));
		if(! S.base )
			exit(OVERFLOW);
		S.top = S.base + S.stacksize;
		S.stacksize += Increment;
	}
	*S.top = e;
	S.top++;
	return OK;
} 

//出栈
Status Pop(SqStack &S, SElemType &e)
{
	if(S.base == S.top)
		return ERROR;
	e = *(S.top - 1);
	S.top--;
	return OK;
} 

int main()
{
	SqStack S;
	SElemType e;
	int len;
	InitStack(S);
	printf("the stack is:");
	if(StackEmpty(S))
		printf(" empty.n");
	else
		printf(" not empty.n");
	Push(S, 'a');
	Push(S, 'b');
	Push(S, 'c');
	Push(S, 'd');
	Push(S, 'e');
	Push(S, 'f');
	
	printf("the stack's length is:");
	len = StackLength(S);
	printf("%dn",len);
	printf("the stack is:");
	while(! StackEmpty(S))
	{
		Pop(S, e);
		printf("%c  ",  e);
	}
	printf("nstack's area = %dn",S.stacksize );
	printf("销毁栈n");
	DestroyStack(S);
	printf("the stack is：");
	while(! StackEmpty(S))
	{
		Pop(S, e);
		printf("%c  ",e);
	} 
	printf("stack's area = %dn",S.stacksize );
	system("pause");
	
	return 0;
}

在这里插入图片描述

链栈

1)链栈的基本特性及概念
链栈：就是栈的链式存储结构，简称链栈。
首先我们要考虑的就是链栈的存储结构，由于栈只是在栈顶进行插入和删除操作，而且单链表也存在头指针，栈也存在栈顶指针，那么我们能不能想办法让这二者合为一体呢，答案是肯定的。我们直接将栈顶放在单链表的头部，因此单链表中常用的头指针自然也就失去了意义，通常对链栈来讲是不需要头结点的。对于链栈来讲基本很少出现栈满的情况（除非内存已经被沾满），对于链表来说，链表为空的表示是头结点指向空，那么对于链栈来讲，链栈为空就是栈顶指针指向空（top = NULL）。
2)链栈对顶栈的基本操作及实现(初始化、出入栈、栈是否为空、获取栈顶元素、弹出栈顶元素)

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <malloc.h>

typedef int Status;
typedef int SElemType;
typedef struct StackNode{
	SElemType data;
	struct StackNode *next;
} StackNode, *LinkStack;

Status InitStack(LinkStack &S)
{
	S = NULL;		//生成空栈，单链表表头作为栈顶
	return 1; 
}

//入栈 
Status Push(LinkStack &S, SElemType e)
{
	StackNode *p;
	p = new StackNode;	//生成新结点
	p->data = e;
	p->next = S;
	S = p;
	return 1; 
}

void PushToStack(LinkStack &S)
{
	int n, flag;
	SElemType e;
	printf("请输入入栈元素个数（>=1）：n");
	scanf("%d", &n);
	for(int i =1; i <= n; i++)
	{
		printf("请输入第%d个元素的值", i);
		scanf("%d", &e);
		flag = Push(S, e);
		if(flag)
			printf("%d已入栈n", e);
	} 
}

//出栈
bool Pop(LinkStack &S, SElemType &e)
{
	LinkStack p;
	if(S == NULL)
		return false;
	e = S->data;
	p = S;
	S = S->next;
	free(p);
	return true;
} 

void PopFromStack(LinkStack &S)
{
	int n, flag;
	SElemType e;
	printf("请输入出栈元素个数(>=1)：");
	scanf("%d", &n);
	for(int i = 1; i <= n; i++)
	{
		flag = Pop(S, e);
		if(flag)
			printf("%d已出栈n", e);
		else{
			printf("栈空n");
			break;
		}
	}
}

//取栈顶
bool GetTop(LinkStack &S, SElemType &e)
{
	if(S == NULL)
		return false;
	e = S->data;
	return true;
} 

void GetTopOfStack(LinkStack S)
{
	SElemType e;
	bool flag;
	flag = GetTop(S, e);
	if(flag)
		printf("栈顶元素为：%dn", e);
	else
		printf("栈空n");		
}

int main()
{
	LinkStack S;
	InitStack(S);
	PushToStack(S);
	PopFromStack(S);
	GetTopOfStack(S);
	system("pause");
	
	return 0;
}

队列

队列介绍

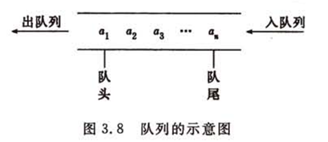
队列也是一种线性表，是一种先进先出(FIFO) 的线性结构。队列只允许在表的一端进行插入（入队）、删除（出队）操作。允许插入的一端称为队尾，允许删除的一端称为队头。

队列有两种存储形式：顺序存储和链式存储。采用顺序队列存储的队列称为顺序队列，采用链式存储的队列称为链式队列。顺序队列采用数组存储队列中的元素，使用两个指针头指针（front）和尾指针(rear)分别指向队列的队头和队尾。使用顺序队列由于在操作时会出现“假溢出现象”，所以可以使用顺序循环队列合理的使用队列空间。链式队列使用链表来实现，链表中的数据域用来存放队列中的元素，指针域用来存放队列中下一个元素的地址，同时使用队头指针指向队列的第一个元素和最后一个元素。
在这里插入图片描述

顺序队列

代码：

#include <stdio.h>
#include <assert.h>
#include <stdlib.h>
#define MaxSize 10  //定义队列的最大容量，等等验证假溢出

typedef int DataType;  //定义队列中元素类型
typedef struct Queue
{
    DataType Queue[MaxSize];
    int front, rear;
}SeqQueue;

//队列初始化，将队列初始化为空队列
void InitQueue(SeqQueue *SQ)
{
    SQ->front = SQ->rear = 0;  //把队头和队尾指针同时置为0
}

//判断队列是否为空
int IsEmpty(SeqQueue *SQ)
{
    if(SQ->front == SQ->rear)
    {
        return 1;
    }
    return 0;
}

//判断队列是否为满
int IsFull(SeqQueue *SQ)
{
    if(SQ->rear == MaxSize)
    {
        return 1;
    }
    return 0;
}

//入队,将元素data插入到队列SQ中
int EnterQueue(SeqQueue *SQ,DataType data)
{
    if(IsFull(SQ))
    {
        printf("队列已满n");
        return 0;//加上这一句，否则后续打印会发生错误
    }
    SQ->Queue[SQ->rear] = data;  //在队尾插入元素data
    SQ->rear = SQ->rear + 1;     //队尾指针后移一位
}

//出队，将队列中队头的元素data出队，出队后队头指针front后移一位
int DeleteQueue(SeqQueue *SQ,DataType *data)
{
    if (IsEmpty(SQ))
    {
        printf("队列为空！n");
        return 0;
    }
    *data = SQ->Queue[SQ->front];   //出队元素值
    SQ->front = (SQ->front)+1;      //队尾指针后移一位
    return 1;
}

//获取队首元素
int GetHead(SeqQueue *SQ,DataType *data)
{
    if (IsEmpty(SQ))
    {
        printf("队列为空!n");
    }
    return *data = SQ->Queue[SQ->front];
}

//清空队列
void ClearQueue(SeqQueue *SQ)
{
    SQ->front = SQ->rear = 0;
}

//打印队列中的元素
void PrintQueue(SeqQueue *SQ)
{
    assert(SQ);//发生错误则终止程序（常用于进行异常处理）
    int i = SQ->front;
    while(i < SQ->rear)
    {
        printf("%d  ", SQ->Queue[i]);
        i++;
    }
    printf("n");
}

int main()
{
    SeqQueue SQ;
    DataType data;
    //初始化队列
    InitQueue(&SQ);
    //入队
    EnterQueue(&SQ, 1);
    EnterQueue(&SQ, 2);
    EnterQueue(&SQ, 3);
    EnterQueue(&SQ, 4);
    EnterQueue(&SQ, 5);
    EnterQueue(&SQ, 6);
    EnterQueue(&SQ, 8);
    EnterQueue(&SQ, 10);
    EnterQueue(&SQ, 12);
    EnterQueue(&SQ, 15);

    //打印队列中的元素
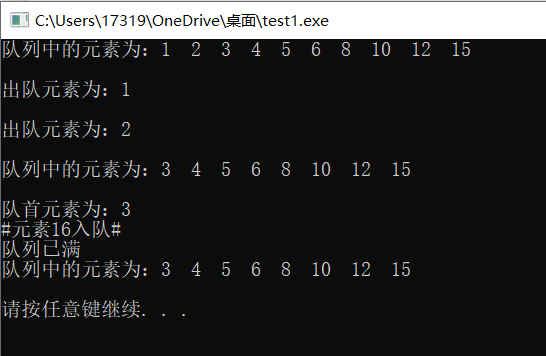
    printf("队列中的元素为：");
    PrintQueue(&SQ);
    printf("n");
    //出队
    DeleteQueue(&SQ, &data);
    printf("出队元素为：%dn", data);
    printf("n");
    DeleteQueue(&SQ, &data);
    printf("出队元素为：%dn", data);
    printf("n");
    printf("队列中的元素为：");
    PrintQueue(&SQ);
    printf("n");
    //获取队首元素
    data = GetHead(&SQ, &data);
    printf("队首元素为：%dn", data);
    printf("#元素16入队#n");
    //元素16入队
    EnterQueue(&SQ, 16);
    printf("队列中的元素为：");
    PrintQueue(&SQ);
    printf("n");
    system("pause");
    
    return 0;
}

在这里插入图片描述

顺序循环队列

在上面顺序队列的代码里，我们定义的队列的最大容量为：10，依此调用入队函数EnterQueue，将1，2，3，4，5，6，8，10，12，15总共10个元素依此入队，我们看到运行结果最先输出队列已满，这是因为15入队时，队列以达到最大容量，所以，输出提示信息“队列已满”，打印队列中的元素结果入第二行1，2，3，4，5，6，8，10，12，15。然后依此测试了出队，取队首元素等函数，仔细观察，可以发现在测试出队时，依此出队两次，此时打印队列中的元素值为3，4，5，6，8，10，12，15总共8个元素值。我们定义的队列的最大容量为10，出队两次后队列中的元素个数为8，则队列中还有两个空间，但再次执行入队操作EnterQueue(&SQ, 16); 发现并没有将16成功入队，而是输出提示“队列已满”，再次打印队列中的元素，发现队列中依然只有8个元素。这时怎么回事儿呢？其实这就是顺序队列的“假溢出现象”。
假溢出介绍：所谓假溢出现象，即队头由于出队操作，还有剩余空间，但队尾指针已达到数组的末尾，如果继续插入元素，队尾指针就会越出数组的上界，而造成“溢出”，这种溢出不是因为存储空间不够而产生的溢出，而是经过多次插入删除操作引起的，像这中有存储空间而不能插入元素的操作称为“假溢出“。可以通过下面的图爿理解假溢出。
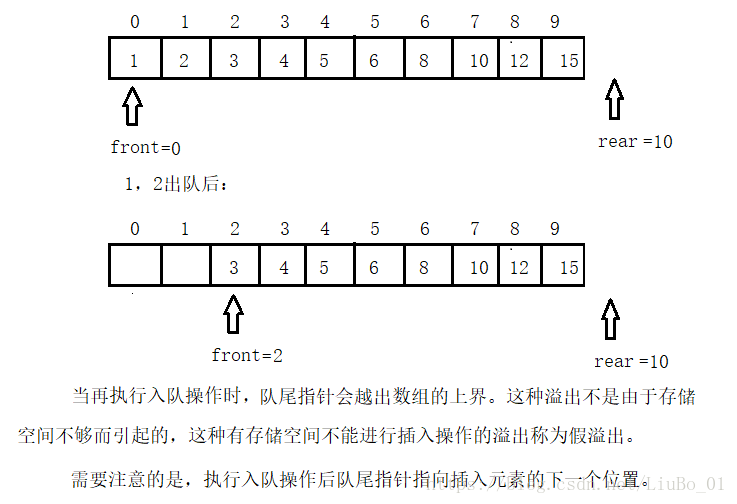
在这里插入图片描述
为了充分利用存储空间，消除这种”假溢出”,可以采用的方法是：将为队列分配的空间看成为一个首尾相接的圆环，并称这种队列为循环队列。
在循环队列中进行出队、入队操作时，队首、队尾指针仍要加1，指针移动。只不过当队头指针front 指向向量上界(MaxSize-1)时，其加1操作的结果是指向向量的下界0。
这种循环意义下的加1操作可以描述为：

if (i + 1 == MaxSize) i=0;
else i++ ;

循环队列利用数学上的取模运算将首尾巧妙相连：i = ( i + 1 ) % Maxsize;这样循环队列所分配的空间可以被充分利用，除非向量空间真的被队列元素全部占用，否则不会上溢。
但注意，循环队列在队空和队满时，都是队头指针和队尾指针指向同一个位置，即：front==rear 为了区分这两种情况，可以少用一个存储空间 （如本题本来是10个存储空间，但队满时只用了9个），队空的判断条件不变，以队尾指针rear加1等于队头指针为队列的判满条件。即：front = rear 表示队空，（rear + 1) % MaxSize == fornt 表示队满。

代码：

#include <stdio.h>
#include <assert.h>
#include <stdlib.h>
#define MaxSize 10

typedef int DataType;
typedef struct SeqQueue{
	DataType Queue[MaxSize];
	int front, rear;
}SeqCirQueue;

//初始化
void InitSeqCirQueue(SeqCirQueue *SCQ)
{
	
	SCQ->front = SCQ->rear = 0;
}

//判断队列是否为空
int IsEmpty(SeqCirQueue *SCQ)
{
	if(SCQ->front == SCQ->rear )
	{
		return 1;
	}
	return 0;
}

//判断队列是否为满
int IsFull(SeqCirQueue *SCQ)
{
	if((SCQ->rear + 1) % MaxSize == SCQ->front)
	{
		return 1;
	}
	return 0;
} 

//入队操作
int EnterSeqCirQueue(SeqCirQueue *SCQ,  DataType data)
{
	if(IsFull(SCQ))
	{
		printf("队列已满，无法完成入队操作n");
		return 0;
	}
	SCQ->Queue[SCQ->rear] = data;
	SCQ->rear = (SCQ->rear + 1) % MaxSize;
} 

//出队操作
int DeleteSeqCirQueue(SeqCirQueue *SCQ, DataType *data)
{
	if(IsEmpty(SCQ))
	{
		printf("队列为空，无法完成出队操作n");
		return 0;
	}
	*data = SCQ->Queue[SCQ->front];
	SCQ->front = (SCQ->front +1) % MaxSize;
} 

int LenSeqCirQueue(SeqCirQueue *SCQ)   //计算队的长度
{
	int i;
	i = (SCQ->rear - SCQ->front + MaxSize) % MaxSize;
	return i;
}

//取队首元素
int GetHead(SeqCirQueue *SCQ, DataType *data)
{
	if(IsEmpty(SCQ))
	{
		printf("队列为空n");
		return 0;
	}
	*data = SCQ->Queue[SCQ->front ];
	return *data;
} 

//清空队列
void ClearSeqCirQueue(SeqCirQueue *SCQ)
{
    SCQ->front = SCQ->rear = 0;
}

//打印队列内元素
void PrintSeqCirQueue(SeqCirQueue *SCQ)
{
	assert(SCQ);
	int i = SCQ->front;
	if(SCQ->front < SCQ->rear )
	{
		for(; i < SCQ->rear; i++)
			printf("%d   ",SCQ->Queue[i]);
	}
	else
	{
		for(i; i < SCQ->rear + MaxSize; i++)
			printf("%d   ",SCQ->Queue[i]);
	}
	printf("n");
} 

int main()
{
	SeqCirQueue SCQ;
	InitSeqCirQueue(&SCQ);
	int len;
	EnterSeqCirQueue(&SCQ, 1);
	EnterSeqCirQueue(&SCQ, 2);
	EnterSeqCirQueue(&SCQ, 3);
	EnterSeqCirQueue(&SCQ, 4);
	EnterSeqCirQueue(&SCQ, 5);
	EnterSeqCirQueue(&SCQ, 6);
	EnterSeqCirQueue(&SCQ, 7);
	EnterSeqCirQueue(&SCQ, 8);
	EnterSeqCirQueue(&SCQ, 9);
	printf("打印队列内元素：n");
	PrintSeqCirQueue(&SCQ);
	EnterSeqCirQueue(&SCQ, 10);
	DataType data;
	DeleteSeqCirQueue(&SCQ, &data);
	printf("出队元素%dn",data);
	printf("打印队列内元素：n");
	PrintSeqCirQueue(&SCQ);
	EnterSeqCirQueue(&SCQ, 11);
	printf("队列中元素：n");
	PrintSeqCirQueue(&SCQ);
	printf("队首元素：");
	data = GetHead(&SCQ, &data);
	printf("%dn",data);
	printf("队列长度：");
	len = LenSeqCirQueue(&SCQ);
	printf("%dn",len);
	system("pause");	
	
	return 0;
}

233

链式队列

#include <stdio.h>
#include <assert.h>
#include <stdlib.h>
#define OK 1
#define ERROR 0
#define OVERFLOW -1

typedef int Status;
typedef int QElemType;
typedef struct Node{
	QElemType data;
	struct Node *next;
} QNode;

typedef struct{
	QNode *front, *rear;
} LinkQueue;

//初始化 
Status InitQueue(LinkQueue *LQ)
{
	LQ->front = LQ->rear = (QNode*)malloc(sizeof(QNode));
	if(! LQ->front)
		exit(OVERFLOW);
	LQ->rear->next = NULL;
	return OK;
}

//判断队列是否为空
Status EmptyQueue(LinkQueue LQ)
{
	if(LQ.front->next == NULL)
		printf("the queue is empty.n");
	return OK;
} 

//入队
Status EnterQueue(LinkQueue *LQ, int elem)
{
	QNode *p;
	p = (QNode*)malloc(sizeof(QNode));
	p->data = elem;
	p->next = NULL;
	LQ->rear->next = p;
	LQ->rear = p;
	return OK;
} 

//出队
Status OutQueue(LinkQueue *LQ)
{
	QNode *p;
	p = LQ->front;
	LQ->front = LQ->front->next;
	free(p);
	p = NULL;
	return OK; 
} 

//打印队列元素
Status PrintQueue(LinkQueue LQ)
{
	QNode *p;
	p = LQ.front->next;
	printf("the queue is:");
	while(p != NULL)
	{
		printf("%d  ",p->data );
		p = p->next;
	} 
	printf("n");
	return OK;
} 

int main()
{
	LinkQueue LQ;
	int elem;
	InitQueue(&LQ);
	EnterQueue(&LQ, 1);
	EnterQueue(&LQ, 2);
	EnterQueue(&LQ, 3);
	EnterQueue(&LQ, 4);
	EnterQueue(&LQ, 5);
	EnterQueue(&LQ, 6);
	EnterQueue(&LQ, 7);
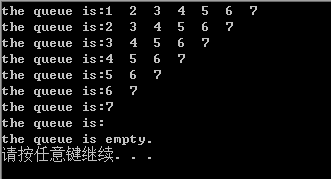
	PrintQueue(LQ);
	
	OutQueue(&LQ);PrintQueue(LQ);
	OutQueue(&LQ);PrintQueue(LQ);	
	OutQueue(&LQ);PrintQueue(LQ);	
	OutQueue(&LQ);PrintQueue(LQ);
	OutQueue(&LQ);PrintQueue(LQ);	
	OutQueue(&LQ);PrintQueue(LQ);	
	OutQueue(&LQ);PrintQueue(LQ);	

	EmptyQueue(LQ);
	system("pause");
	
	return 0;
}

在这里插入图片描述

栈是限定在表尾进行插入和删除操作的线性表允许插入和删除的一端为栈顶，另一端为栈底，出栈元素只能是栈顶元素，后进先出，相邻元素具有前驱与后继关系.。

队列是只允许在一端进行插入操作，在另一端进行删除操作的线性表。允许插入的一端为队尾，允许删除的一端为队头，先进先出，相邻元素具有前驱与后继关系。

本文参考资料：
栈的基本介绍
数据结构：顺序表、单链表、栈和队列的简单总结
队列的基本操作（顺序队列、循环队列、链式队列）

最后

以上就是自信黄蜂为你收集整理的栈和队列实验目的栈队列的全部内容，希望文章能够帮你解决栈和队列实验目的栈队列所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。

本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。

本文分类：study
浏览次数：65 次浏览
发布日期：2023-10-03 09:15:51
本文链接：https://www.kaopuke.com/article/k-p-k_14_uzogf1_14_j_14_4.html

栈和队列实验目的栈队列

概述

数据结构学习——栈与队列

实验目的

栈

栈的介绍

顺序栈

链栈

队列

队列介绍

顺序队列

顺序循环队列

链式队列

最后

评论列表共有 0 条评论

发表评论取消回复

栈和队列实验目的栈队列

概述

数据结构学习——栈与队列

实验目的

栈

栈的介绍

顺序栈

链栈

队列

队列介绍

顺序队列

顺序循环队列

链式队列

最后

相关文章

评论列表共有 0 条评论

发表评论 取消回复

发表评论取消回复