Gaussian Mixture Model ,就是假设数据服从 Mixture Gaussian Distribution ,换句话说,数据可以看作是从数个 Gaussian Distribution 中生成出来的。实际上,我们在 K-means 和 K-medoids 两篇文章中用到的那个例子就是由三个 Gaussian 分布从随机选取出来的。实际上,从中心极限定理可以看出,Gaussian 分布(也叫做正态 (Normal) 分布)这个假设其实是比较合理的,除此之外,Gaussian 分布在计算上也有一些很好的性质,所以,虽然我们可以用不同的分布来随意地构造 XX Mixture Model ,但是还是 GMM 最为流行。另外,Mixture Model 本身其实也是可以变得任意复杂的,通过增加 Model 的个数,我们可以任意地逼近任何连续的概率密分布。
每个 GMM 由 个 Gaussian 分布组成,每个 Gaussian 称为一个“Component”,这些 Component 线性加成在一起就组成了 GMM 的概率密度函数:
P
(
x
∣
θ
)
=
∑
n
=
1
N
c
m
N
(
x
∣
θ
m
)
P(x | theta)=sum_{n=1}^{N} c_{m} mathrm{N}left(x | theta_{m}right)
P(x∣θ)=n=1∑NcmN(x∣θm)
其中Cm是权重,X是样本,θm表示第m个子模型的参数集,包含平均值以及协方差
(
μ
m
,
Σ
n
)
left(mu_{m}, Sigma_{n}right)
(μm,Σn)
根据上面的式子,如果我们要从 GMM 的分布中随机地取一个点的话,实际上可以分为两步:首先随机地在这 个 Component 之中选一个,每个 Component 被选中的概率实际上就是它的系数 ,选中了 Component 之后,再单独地考虑从这个 Component 的分布中选取一个点就可以了──这里已经回到了普通的 Gaussian 分布,转化为了已知的问题。
那么如何用 GMM 来做 clustering 呢?其实很简单,现在我们有了数据,假定它们是由 GMM 生成出来的,那么我们只要根据数据推出 GMM 的概率分布来就可以了,然后 GMM 的 个 Component 实际上就对应了 个 cluster 了。根据数据来推算概率密度通常被称作 density estimation ,特别地,当我们在已知(或假定)了概率密度函数的形式,而要估计其中的参数的过程被称作“参数估计”。
matlab代码如下:
%% 初始化工作空间
clc
clear all
close all
%% 载入数据
load fisheriris
%% 二维数据
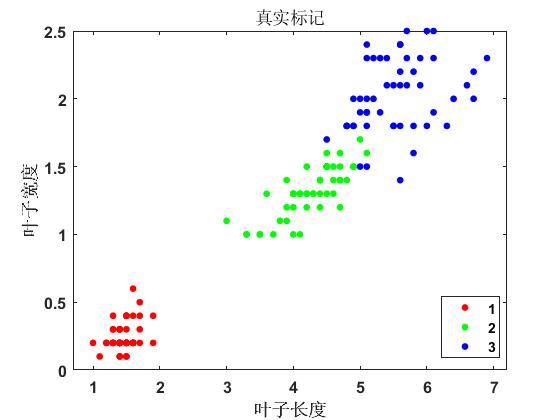
% 叶子长度和叶子宽度散点图(真实标记)
figure;
speciesNum = grp2idx(species);
gscatter(meas(:,3),meas(:,4),speciesNum,['r','g','b'])
xlabel('叶子长度')
ylabel('叶子宽度')
title('真实标记')
set(gca,'FontSize',12)
set(gca,'FontWeight','bold')
% 叶子长度和叶子宽度散点图(无标记)
figure;
scatter(meas(:,3),meas(:,4),150,'.')
xlabel('叶子长度')
ylabel('叶子宽度')
title('无标记')
set(gca,'FontSize',12)
set(gca,'FontWeight','bold')
%% 高斯混合模型聚类
data = [meas(:,3), meas(:,4)];
% 手动初始条件
Mu=[0.25 1.5; 4.0 1.25; 5.5 2.0 ];%平均值设定
Sigma(:,:,1) = [1 1;1 2];%方差设定
Sigma(:,:,2) = [1 1;1 2];
Sigma(:,:,3) = [1 1;1 2];
Pcom=[1/3 1/3 1/3];%混合比例
S = struct('mu',Mu,'Sigma',Sigma,'ComponentPropotion',Pcom);
GMModel = fitgmdist(data,3,'Start',S);
% 分类
T1 = cluster(GMModel,data);
% 标号调整
cen=[mean(data(T1==1,:));...
mean(data(T1==2,:));...
mean(data(T1==3,:))];
dist=sum(cen.^2,2);
[dump,sortind]=sort(dist,'ascend');
newT1=zeros(size(T1));
for i =1:3
newT1(T1==i)=find(sortind==i);
end
% 叶子长度和叶子宽度散点图(真实标记:实心圆+kmeans分类:圈)
figure;
gscatter(meas(:,3),meas(:,4),speciesNum,['r','g','b'])
hold on
gscatter(data(:,1),data(:,2),newT1,['r','g','b'],'o',10)
scatter(cen(:,1),cen(:,2),300,'m*')
hold off
xlabel('叶子长度')
ylabel('叶子宽度')
title('真实标记:实心圆+kmeans分类:圈')
set(gca,'FontSize',12)
set(gca,'FontWeight','bold')
%% 混淆矩阵 ConfusionMatrix
T2ConfMat=confusionmat(speciesNum,newT1)
error23=(speciesNum==2)&(newT1==3);
errDat23=data(error23,:)
error32=(speciesNum==3)&(newT1==2);
errDat32=data(error32,:)
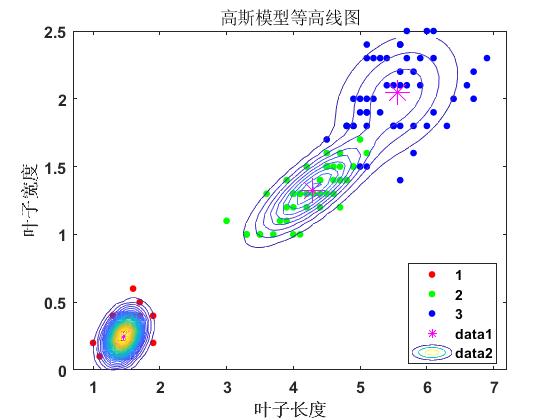
%% 高斯模型等高线图
% 散点图
figure;
gscatter(meas(:,3),meas(:,4),speciesNum,['r','g','b'])
hold on
scatter(cen(:,1),cen(:,2),300,'m*')
hold off
xlabel('叶子长度')
ylabel('叶子宽度')
title('高斯模型等高线图')
set(gca,'FontSize',12)
set(gca,'FontWeight','bold')
% 叠加等高线
haxis=gca;
xlim = get(haxis,'XLim');
ylim = get(haxis,'YLim');
dinter=(max([xlim, ylim]) - min([xlim, ylim]))/100;
[Grid1, Grid2] = meshgrid(xlim(1):dinter:xlim(2), ylim(1):dinter:ylim(2));
hold on
GMMpdf=reshape(pdf(GMModel, [Grid1(:) Grid2(:)]), size(Grid1,1), size(Grid2,2));
contour(Grid1, Grid2, GMMpdf, 30);
hold off
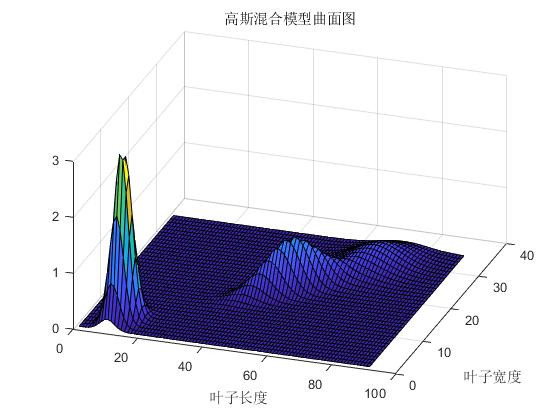
% 混合高斯模型曲面图
figure;
surf(GMMpdf)
xlabel('叶子长度')
ylabel('叶子宽度')
title('高斯混合模型曲面图')
view(-3,65)
结果显示:
最后
以上就是风趣世界最近收集整理的关于高斯混合模型聚类(GMM)matlab实现的全部内容,更多相关高斯混合模型聚类(GMM)matlab实现内容请搜索靠谱客的其他文章。








发表评论 取消回复