目录

1.二叉树的基本定义:

1.1二叉树的一些性质:

2.二叉树的实现:

3.关于二叉树的遍历方式

4.一些特殊类型的二叉树

(1)完全二叉树

(2)二叉排序/搜索树

(3)AVL树(平衡二叉搜索树)

5.二叉树的一些算法和方法原理

6.关于二叉树的应用

(1)信号放大器

(2)在线等价类

---

1.二叉树的基本定义:

二叉树的定义为,每个结点的左右孩子最多为两个,也叫做黑红树

1.1二叉树的一些性质:

(1)n个元素的二叉树边数为n-1

(2)树的高度为h时,树的高度最大为h,最小为logh-1

(3)n的元素的最大高度为n,最小高度为logn+1(完全二叉树的形态)

2.二叉树的实现:

(1)二叉树的建立方式同样是使用递归方法,常用的是前序遍历

这里引入"#"符号,代表二叉树的这个位置什么都没有可以跳过

代码如下

class Tree {
public:
	char name;
	Tree* lchird;
	Tree* rchird;
};
void createdoubleforktree(Tree*& root) {
	char temp;
	cin >> temp;
	if (temp == '#') {
		root = nullptr;//不用创建新的结点了
	}
	else {
		root = new Tree();
		if (!root)
			exit(OVERFLOW);//内存分配失败则推
		root->name = temp;
		createdoubleforktree(root->lchird);
		createdoubleforktree(root->rchird);
	}
}
int main() {
	Tree* tree;
	createdoubleforktree(tree);
	cout << tree->lchird->name << endl;
}

ps:这里一个要注意的问题就是:传入的是指针的引用,因为内部会对指针进行重新赋值,请详见下方的东西.

比如最开始收到困惑的地方就是这种情况

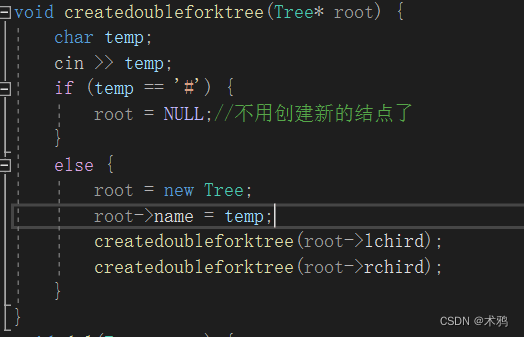
 外界传入的是根节点的地址,形成的效果也就是,root变成一个指向根节点的指针;

但是紧接着在下面的操作中,root的指向又变成了new Tree,而不是外面的根节点(大一上java的考点之一),接下来自然是各玩各的,读取根节点发现还是空的;

问题就在这里,root确实是指向同一个东西并且可以修改里面的数值,但是那是在 解引用 的基础上,直接篡改只能是改变指向,导致程序失效;

破解方法就是

传入指针的引用,而根节点也直接用指针进行表示

传入的是指针的引用,修改里面的时候,外面指针的指向也会发生变化.....

void deckerCreate(treeNode*& root, int n, string target) {
//为了保证完全二叉树的性质,这里不使用第0位!
	if (n <= target.length() - 1) {
		root = new treeNode;
		root->own = target[n];//这里是创建新节点
		deckerCreate(root->left, 2 * n, target);
		deckerCreate(root->right, 2 * n + 1, target);
	}
}

注意一点,二叉树的层序遍历创建虽然也是递归,却是另一种形式,使用完全二叉树的性质,所以我们要配合数组进行使用;

大致的代码逻辑为:每次遍历都读入一个数字,然后给这个结点赋值,再去寻找2i和2i+1两个孩子,进行递归复制;

递归截止的条件为:当前的i数值小于等于输入的长度;

这里给一段代码实现

3.关于二叉树的遍历方式

前序,中序,后序,层序遍历

四种遍历算法的时间复杂性,空间复杂性均为n,因为除了赋值没有啥多余的计算

如一个二叉树            A

                         B               C

前序遍历的结果就是A  B  C,快速排序其实就是一种具体实现;

中序遍历的结果是BAC

后序遍历的结果是B C A,归并排序就是其一种具体的体现;

具体代码实现大同小异,其实就是读取操作放在什么样的位置上,前三种遍历都是殊途同归

void search(Tree* root) {//前序遍历成功
	if (root != NULL) {
		search(root->lchird);
		cout << root->name;
		//先序中序后续的顺序只要修改这个部分就可以了
		search(root->rchird);
	}
}

补充,关于二叉树的层序遍历方法

层序遍历直接用队列来实现就可以,类似BFS的操作,不过简单很多

先把树根节点顶入队列,然后如果队列不空,就读出队列前端的东西并且输出,然后把输出的东西的两个子代(如果有的话)再加入栈中,持续这样的操作直到队列变成空的.

(这里队列里面存的是指针,避免了麻烦的时候也要小心为空这种情况)

void decker(treeNode*& root) {//层序遍历,层序遍历不需要递归来实现
	q.push(root);
	queue<treeNode*> q;
	while (!q.empty()) {
		treeNode* temp = q.front();
		q.pop();
		if (temp != NULL) { //不过这样子复杂度会稍微高一点,可以改进一下
			cout << temp->own;
			q.push(temp->left);
			q.push(temp->right);
		}
	}
}

(3)二叉树的线索化,这里以中序二叉树为例

其实就是对二叉树空指针的利用,如果指向左孩子的指针是空的,就让其指向前驱

同理,右孩子结点指向后驱.在节点处增加一个左右判断域,来判断这个点指向的是孩子还是前后驱.

//这里是一个线索化的操作,按照中序的顺序进行线索化
//这里利用中序遍历创建(0为正常结点,1表示这个指针是空的)
//空的左节点指向前驱动(1),空的右节点指向后继(1)
Tree* pre;//前驱
void thread(Tree* root) {
	if (root != NULL) {
		thread(root->lchird);
		if (root->lchird==NULL) {
			root->ltag == 1;
			root->lchird = pre;
		}
		if (pre!=NULL&&pre->rchird==NULL) {//防止最开始的时候访问前驱出问题,书里可能写错了
			pre->rtag = 1;
			pre->rchird = root;
		}
		pre = root;
		thread(root->rchird);
	}
}

4.一些特殊类型的二叉树

(1)完全二叉树

最常用的一种二叉树,我甚至在怀疑要不要专门记录下来....

二叉树的高度为log(n+1),序号的编写从1开始到n,以层序遍历的方式分配,这种方式的好处是可以利用数组来存储模拟树的结构进行诸如堆排序的操作

其中完全二叉树最常用的性质是

(1)双亲为 i/2

(2)左孩子为2i 右孩子为2i+1

二叉树的描述方式分为链表描述,数组描述

(2)二叉排序/搜索树

二叉排序树是后面的补充内容,利用中序遍历可以顺利读取,树的形状和高度与初始根节点i不可分

(1)排序二叉树的创建/插入

//关于二叉排序树的创建
class TreeNode {
public:
	int num;
	TreeNode* left=NULL;
	TreeNode* right=NULL;
};


void createTree(TreeNode*& root,int num) {//二叉树递归排序的核心,每次插入一个数字都要重新递归一次
	if (root==NULL) {                    // 这其实也是插入操作,,外面套个遍历的方法就是生成操作了
		root = new TreeNode();           //如果真要插入记得加个判断,不要重复输入
		root->num = num;
	}
	else {
		if (num > root->num)
			createTree(root->right,num);
		else if (num < root->num)
			createTree(root->left,num);
	}
}

void create(TreeNode*& root) {//排序二叉树的创建(自动排序)
	int n, num;
	cout << "请输入二叉树的节点数目(能进行简单排列)" << endl;
	cin >> n;
	for (int i = 1; i <= n; i++) {
		cin >> num;
		createTree(root, num);
	}
}

递归的过程和比较查找特别相似.....

(2)查找

//这里说一下二叉排序树的查找并非是遍历
//因为有大小判断左右,一定是单线走完的,所以触及到根部则判断为空
bool search(TreeNode*& root,int key, TreeNode*& target) {//二叉排序树的查找方法
	if(root==NULL) {
	return false;
	}
	else if (root->num == key) {
		target = root;
		return true;
	}
	else if (key > root->num) {
		search(root->right, key, target);
	}
	else if (key < root->num) {
		search(root->left, key, target);
	}
}

(3)删除

按照替换原理,这里使用了两种方法

//二叉排序树的删除方法(中序前驱或者后继替代)
//代码原理,如果一个结点被删除,可以用中序遍历中的前驱和后继进行替代
//前驱:左子树里面最右侧的那个点
//后继:右子树里面最左侧的那个点
void delete_1(TreeNode*& root, int key) {
	TreeNode* point;
	if (!search(root, key, point)) {
		cout << "没有这个点" << endl;
	}
	else {
		if (point->left == NULL) {
			TreeNode* point1 = point;   point = point->right;   delete point1;
		}
		else if (point->right = NULL) {
			TreeNode* point1 = point;   point = point->left;    delete point1;
		}
		else {//这里找前驱作为替代点
			TreeNode* point1 = point;   TreeNode* s = point->left;
			while (s->right) {
				point1 = s; s = s->right;
			}//s为可能的前驱,point1为s的双亲
			point->num = s->num;//前驱数值替换要删除点的数值(不删除这个点,只是修改它的数值)
			//如果前驱就是左孩子,那么直接把左孩子的左孩子接收一下
			if (point1 == point) {
				point1->left = s->left;
			}
			//如果前驱是一般情况,那么就接收为右孩子;
			else {
				point1->right = s->left;
			}
			delete s;
		}
	}
}
void delete_2(TreeNode*& root, int key) {//另一种使用后驱进行替换的方法
	TreeNode* point;
	if (!search(root, key, point)) {
		return;//检索失败
	}
	else {
		if (point->left == NULL) {
			TreeNode* point1 = point; point = point->right; delete point1;
		}
		else if (point->right == NULL) {
			TreeNode* point1 = point; point = point->left; delete point1;
		}
		else {//这里寻找后驱,用后驱来进行替代即可
			TreeNode* point1 = point;
			TreeNode* s = point->right;
			while (s->left) {
				point = s; s = s->left;
			}
			point->num = s->num;
			if (point == point1) {
				point1->right = s->right;
			}
			else {
				point1->left = s->right;
			}
			delete s;
		}
	}
}

(3)AVL树(平衡二叉搜索树)

1.定义:平衡树,指的是树中左右两兄弟的高度差不超过1,也就是每个结点的平衡因子(左子树减去右子树的高度)只能是-1,0,1三种情况

2.类:AVL树本质上还是二叉搜索树,只不过在创建和删除的时候,要时刻保证每个点的平衡因子都是正确的,故在基本属性上,和普通的二叉搜索树没有任何区别.

3.平衡二叉树的修复方法:

(1)找到高度最低的一个,拥有不正常平衡因子的点,这个点就是最小不平衡树的根节点

(2)找到这个点后,我们分成四种情况:LL(左孩子的左子树发生异常)  RR(右孩子的右子树发生异常)

LR(左孩子的右子树发生异常) RL(右孩子的左子树发生异常) 每种情况都有自己的处理方式

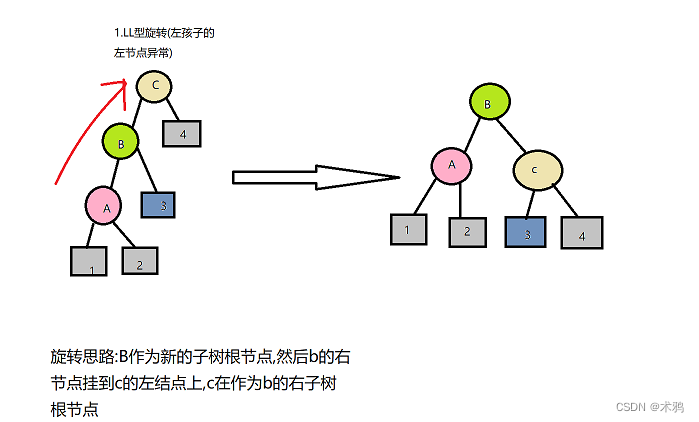
(3)距离,LL形态的处理方法(右旋)

(4)LR的处理方法(先左旋,再右旋) 

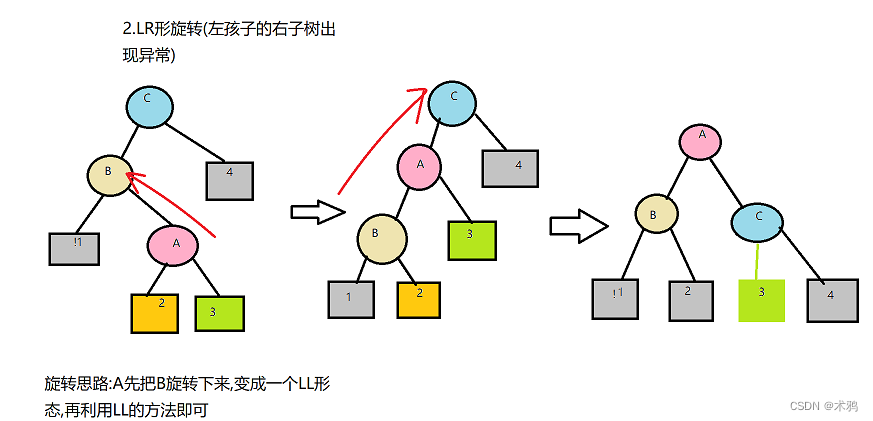
(注意,LL和RR是差不多的,LR和RL是差不多的,这里就不多家赘述了)实现代码详见最后

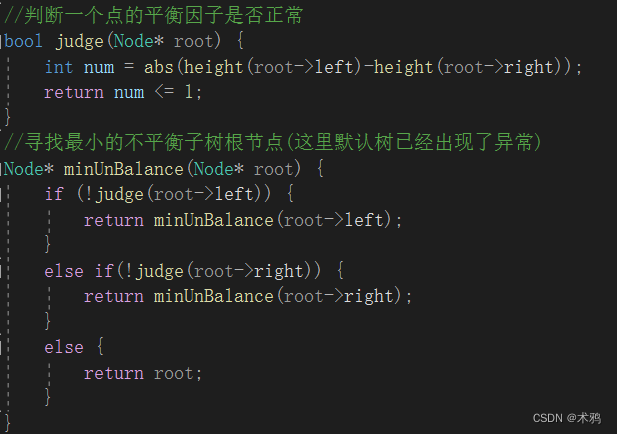
(5)关于找到最小不平衡子树的方法

思路:在使用这个方法之前,在根节点判断一下这个树是不是正常的,因为只要有一个地方有问题,最终会反馈到根节点的平衡因子上面,所以看一眼根节点,确认无误,在开始找

使用递归寻找,如果左右子树的平衡因子都正常,那代表这个点就是问题点,否则哪边有问题就往哪边递归:

代码实现:寻找最小平衡子树根节点

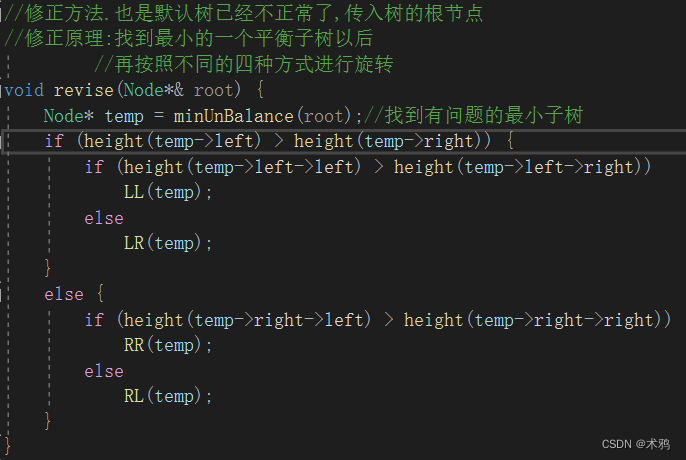
(6)关于判断使用何种旋转方式()修正方法

原理就是,根据两边结点的高度:

如果左节点大于右节点,且左节点的左子树大于右子树,LL

如果左节点大于右节点,且左节点的左子树小于右子树,LR

如果左节点小于右节点,且左节点的左子树大于右子树RL

如果左节点小于右节点,且左节点的左子树小于右子树,RR

代码实现如下

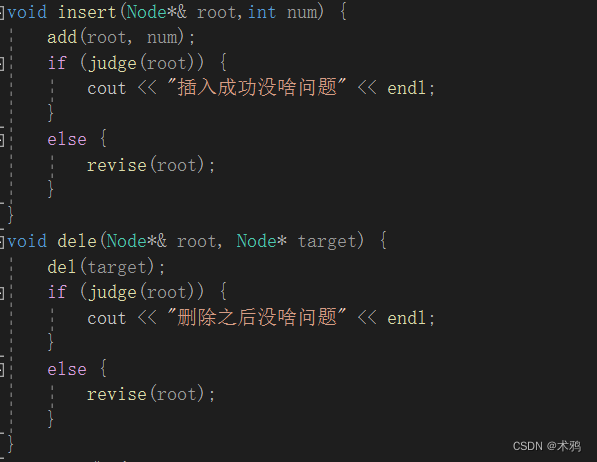
 (7)关于增删方法的原理:

增加方法:先利用二叉搜索树的方法进行插入,然后先判断一下这个树是否平衡,如果平衡就不用管,如果不平衡就进行修正操作

删除方法:利用二叉搜索树的方法进行删除,接下来操作和上面是一样的

(8)关于整体的一个实现代码(太多了应该会折叠) 

//先构建二叉树类型
class Node {
public:
	int num=0;
	Node* parent=NULL;//用不上,平衡因子现场计算吧
	Node* left=NULL;
	Node* right=NULL;
};
class Tree {
public:
	Node* point = NULL;
};
//普通二叉树的方法
void add(Node * point,int num) {
	if (point == NULL) {
		point = new Node; point->num = num;
	}
	else if (point->num > num) {
		add(point->left, num);
	}
	else if (point->num < num) {
		add(point->right, num);
	}
	else {
		cout << "这个点已经存在力" << endl;
	}
};
//查询结点
Node* search(Node* point,int num) {
	if (point == NULL) {
		cout << "不存在这个点" << endl;
		return NULL;
	}
	else if (point->num > num) {
		return search(point->left, num);
	}
	else if (point->num < num) {
		return search(point->right, num);
	}
	else {
		return point;
	}
}
//删除结点
void del(Node*& point) {//参数:根节点,等待删除的结点
	if (point->left == NULL) {
		Node* temp = point; point = point->right; delete temp;
	}
	else if (point->right == NULL) {
		Node* temp = point; point = point->left; delete temp;
	}
	else {//两边均不为空,这里采取的方案为左子树最右面的点进行过替代
		Node* s = point; Node* temp = s->left;
		while (temp->right != NULL) {
			s = temp; temp = temp->right;
		}
		if (s == point) {
			s->left = temp->left;
		}
		else {
			s->right = temp->left;
		}
		delete temp;
	}
}
//计算二叉树高度
int height(Node* root) {
	if (root == NULL)return 0;
	else {
		int l = height(root->left);
		int r = height(root->right);
		if (l >= r) {
			return l + 1;
		}
		else {
			return r + 1;
		}
	}
}
//判断一个点的平衡因子是否正常
bool judge(Node* root) {
	int num = abs(height(root->left)-height(root->right));
	return num <= 1;
}
//寻找最小的不平衡子树根节点(这里默认树已经出现了异常)
Node* minUnBalance(Node* root) {
	if (!judge(root->left)) {
		return minUnBalance(root->left);
	}
	else if(!judge(root->right)) {
		return minUnBalance(root->right);
	}
	else {
		return root;
	}
}
//接下来是四种旋转方式;默认要输入最小的不平衡子树结点!
void LL(Node*& root) {
	Node* temp = root;
	root = root->left;
	temp->left = root->right;
	root->right = temp;
}
void LR(Node*& root) {
	Node* temp = root->left;
	root->left = temp->right;
	temp->right = root->left->left;
	root->left->left = temp;
	LL(root);
}
void RR(Node*& root) {
	Node* temp = root;
	root = root->right;
	temp->right = root->left;
	root->left = temp;
}
void RL(Node*& root) {
	Node* temp = root->right;
	root->right = temp->left;
	temp->left = root->right->right;
	root->right->right = temp;
	RR(root);
}
//修正方法.也是默认树已经不正常了,传入树的根节点
//修正原理:找到最小的一个平衡子树以后
         //再按照不同的四种方式进行旋转
void revise(Node*& root) {
	Node* temp = minUnBalance(root);//找到有问题的最小子树
	if (height(temp->left) > height(temp->right)) {
		if (height(temp->left->left) > height(temp->left->right)) 
			LL(temp);
		else 
			LR(temp);
	}
	else {
		if (height(temp->right->left) > height(temp->right->right)) 
			RR(temp);
		else 
			RL(temp);
	}
}
//AVL树的插入方法
void insert(Node*& root,int num) {
	add(root, num);//先进行正常的增加
	if (judge(root)) {
		cout << "插入成功没啥问题" << endl;
	}
	else {
		revise(root);
	}
}
//AVL树是删除方法
void dele(Node*& root, Node* target) {
	del(target);//先进行正常的删除
	if (judge(root)) {
		cout << "删除之后没啥问题" << endl;
	}
	else {
		revise(root);
	}
}

(4)2-3树

(注:2-3树 234树 b树 b+树这些主要是用于硬盘存储这方面,可以一定程度上简化树的高度,进而减少查找过程,而且太复杂了,这里就不用手动实现了......)

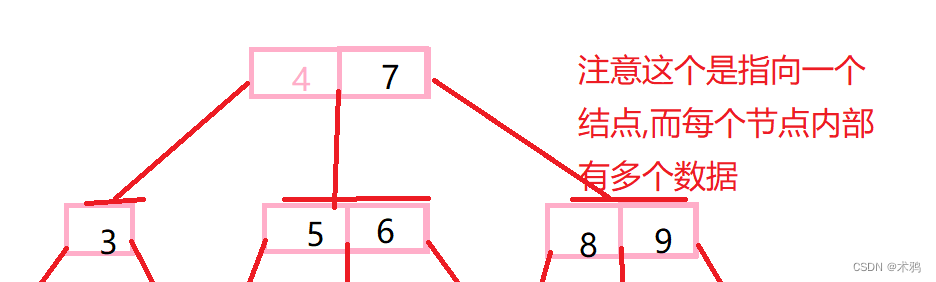
(1)2-3树的定义:

2-3树有两种结点,一种是2结点(两个孩子一个数据)和三结点(三个孩子两个数据)

 2结点要么有两个孩子,要么没有孩子

3结点要么三个孩子都有,要么没有孩子

(关于为什么是2-3后面会补充)

而2-3树本质上仍然是搜索树,单个结点上的数据大小依旧是从左到右,详情请看这个

 (2)23树的插入和删除:这部分情况很复杂,不过可以简单概括一下

插入的工作:和二叉排序树一样,插入的时候一定是在叶子结点进行操作的,所以其实就是:如果叶子节点是2结点,就去按顺序插入元素让他变成3结点,如果要插入的地方已经是3结点了,那么就往双亲上面不断寻找,直到找到一个2结点,然后重新整合一下.或者一直到最顶端都是3结点的时候,然后把根节点拆分,高度加1

删除的工作:类似上面反过来,寻找附近可用的三节点,拆分这个三节点并且想办法补全整个23树,如果没有可用的,则高度会-1,并且合并成新的23树

(注:因为这部分太复杂了,详情可见(大话数据结构)的部分,里面图解可能更清晰一点)

(3)23树的性质:

23树和234树的特点...都是b树的一个特例,详情请看下面b树的部分

(5)B树(很重要!但是我依然不会写代码xd)

(1)B树的定义:B树其实是和硬盘有关的一些数据结构,还是一种多路搜索树,234树等只不过是其中的一种特殊情况罢了;下面是b树的一些性质

1.b树的阶(order):b树的所有节点中最大的孩子数,例如2-3树的阶为3,234树的阶为4

2.k结点:每个结点至少有k-1个数据和k个孩子指针,其中k的取值为

(不小于m/2的最小整数)<= k <=m(m为树的阶)

3.所有的叶子结点都在同一高度(最重要的性质)

(2)b树的应用:

上面说过,b树主要是用于cpu和内存的访存,每次访存的次数不一,反正是很大已经不能用时间复杂度来进行衡量了,如果用二叉树进行存储,那么想要找到一个元素需要访问log(n)次!,这也太多了

所以我们要让一个结点拥有尽可能多的数据位,减少比较往下递归的次数,比如一个1001阶的B树,每个结点最多可以存储1000个数据,那么两层就可以存储上亿条数据,相当于我们只需要递归两次就能找到位置...

当然,你可能就要问了,为什么不直接用1000叉树呢?反而用这种好费力气,唯一可见效果就是高度统一?当然其一是减小高度省空间,其二是利用b+树,方便遍历

(6)b+树的定义,实现和应用

(1)b+树的定义:为了适应系统文件需求对b树进行的存储和遍历,严格来说已经不能称之为树了

(2)实现方式:每一个分支节点中的元素,都会在其中序遍历前继结点的后面再次列出,到最后叶子结点上就会显示所有的数据,此外,叶子节点从左到右都有一条指针,类似这个样子

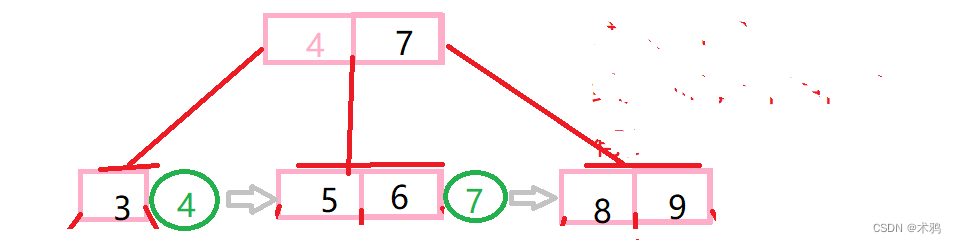
(3)注意,所有的分支结点都视为索引,不能提供访问和存储,必须在叶子结点进行访问存储,也就是说比如我想读取7这个数字即使到了7这个位置,也不能提供访存记录,只能是读取到叶子结点,才能进行访问存储.

不过这种数据结构最适合范围查找了,比如寻找3-7,从根节点开始搜索到叶子结点的3,再从叶子结点的3顺着链表一直到7,中间3-7不需要中序遍历

(B+树也不好实现)

 

5.二叉树的一些算法和方法原理

1.利用顺序创建二叉树

这里补充一个内容,对应的是leetcode对应105,106题目,

利用前序/后序 + 中序来确定一个二叉树并且储存

前序遍历的特点:对于每一个子树来说,第一个点就代表子树的头节点

后序遍历的特点:对于每个子树来说,最后一个点就代表子树的头节点

中序遍历的特点:如果确定了根节点,那么左右分别就是左子树,右子树

1.利用前序和中序的遍历

代码逻辑,先利用before的第一个点(树的根节点),然后找到middle(中序顺序的字符串)中找到这个结点的所在位置n.

接下来可以根据这个middle数组就可以直到左右子树的长度,对应before里面也找到这个子树

before: A BCDEFG

middle:EDBC A GF

举个例子,A在0位,在middle中在第四位,所以可以找到左子树的长度为4,右子树的长度为2

所以可以发现,左子树的前序遍历结果为BCDE,中序为(EDBC)

右子树的前序结果为FG,中序为GF(这个是随便写的,别在意......)

以此类推,往下不断递归寻找,然后创建即可,代码如下

void before_middle(treeNode*& root, string before, string middle, int a, int b, int x, int y) {
	if (a <= b) {
		root = new treeNode;
		root->own = before[a];
		int n = x;
		while (before[a] != middle[n])n++;
		before_middle(root->left, before, middle, a + 1, a + n - x, x, n - 1);
		before_middle(root->right, before, middle, a + n - x + 1, b, n + 1, y);
	}
}

2.利用中序和后序的方式,可以去看笔者的leetcode里面

3.前序和后序是没法确定唯一的二叉树,利口(889)题

关于二叉树的高度计算

二叉树高度计算的原理,同样使用递归,前中后序均可.

返回的是整数类型:当前结点所在的高度=上一个结点返回的高度+1(也就是自己这一层占的高度)

具体判断如下:

如果当前结点为null,则返回0,意为这里目前高度为0

如果当前结点不是null,可以获得左右子树的高度,哪边比较大,就把哪边当作真高度,然后把子树的高度加上1,再返回给上一层

代码如下

//关于二叉树高度的计算:
//原理稍后整理
int height(Node*& root) {
	if (root == NULL)return 0;
	else {
		int l = height(root->left);
		int r = height(root->right);
		if (l > r) {
			return ++l;
		}
		else {
			return ++r;
		}

	}
}

输出叶子节点

一个是输出叶子结点(原理就是遍历如果一个点不是null而且左右全为null,这就是个叶子结点)

//输出所有叶结点
void leaf(Node*& root) {
	if (root != NULL) {
		if (root->left == NULL&&root->right==NULL) {
			cout << root->num;
		}
		else {
			leaf(root->left);
			leaf(root->right);
		}
	}
}

寻找最近的共同祖先,这个需要创建树的时候自带一个parent的指针领域

原理就是双重遍历,a的祖先是大循环,如果b的某个祖先等于当前的祖先,这个就是他们两人的共同祖先,(注意每次都要重置里面的哪个)

//找到两个结点的最近祖先(父母)
Node* anec(Node*& a, Node*& b) {
	Node* temp;
	while (a != NULL) {
		temp = b;//这里记得每次重置
		while (temp != NULL) {
			if (a->num == temp->num) {
				cout <<"共同的结点为:" << a->num << endl;
				return a;
			}
			temp = temp->parent;
		}
		a = a->parent;
	}
}

6.关于二叉树的应用

(1)信号放大器

(待定,感觉用不上)

(2)在线等价类

在线等价类同样是数组实现更加方便一点

二叉树实现的话效果差不多,find找到根节点,如果两个点的根结点不一致,就进行合并,如果一致我们就不要管了.....,不过可以进行优化

最后

以上就是深情黑猫为你收集整理的数据结构--二叉树的基础(预习内容)1.二叉树的基本定义:2.二叉树的实现:3.关于二叉树的遍历方式4.一些特殊类型的二叉树5.二叉树的一些算法和方法原理6.关于二叉树的应用的全部内容，希望文章能够帮你解决数据结构--二叉树的基础(预习内容)1.二叉树的基本定义:2.二叉树的实现:3.关于二叉树的遍历方式4.一些特殊类型的二叉树5.二叉树的一些算法和方法原理6.关于二叉树的应用所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。