这是我第一篇，之前写这个真是一脸懵，只记得我9点写到第二天四点 我不喜欢我的程序因为用户输入了一些特殊的情况就挂 所以一个程序无论多小我都会加上排错的函数。
这个代码可以输出哈夫曼形成的二叉树（好像不能称为树，管他呢）。感觉还是不错的··~
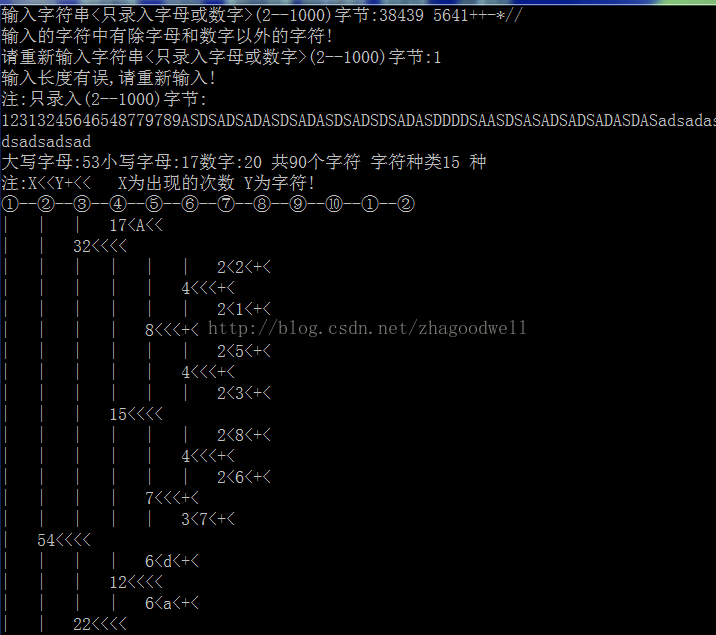
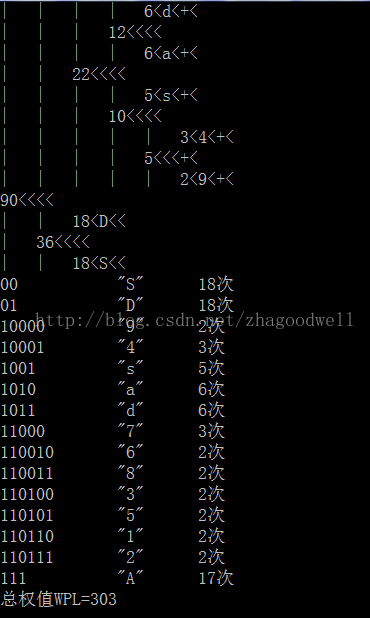
不多说上代码：
复制代码
1
2
3
4/* 制作者zha good well 输入一段字符串对字符串的字符种类和个数进行整理，并输出编码值 哈夫曼编码*/
纯C语言：
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209# include <stdio.h> # include <stdlib.h> # define N 1000 //如果想录入x个字节那么就把N的数值改成x # define M 13 //哈夫曼树编码的长度 typedef struct ptree //定义二叉树结点类型 { struct ptree *lchild; //左0右1子结点指针 struct ptree *rchild; //右子结点指针 int w; //w[2]存储节点权值 char zha[2]; //存储当前的字符 }Ptree,*Optree; //optimum tree typedef struct pforest //每个此类结构体连接一个二叉树与另一个此类结构体 { struct pforest *link; //连接每个叶子节点节点权值由大到小排列 struct ptree *root; //指向叶子节点 }Forest,*forest; int gainchar(char *A,int min,int max);//返回字符长度 范围[min,max] int jianyan(char *ch,int type[3]);//检验字符串是否合法合法的话type[0]=大写字母个数，type[1]=小写字母个数，type[2]=数字字符个数 int BF(char *a,char *b);//字符串匹配 返回匹配的b在a中的个数 int zhengli(char b[],char *p,int *q);//整理字符串,所有可以出现的字符整理到p里,p[i]的次数储存在q[i]中,返回字符串中不同的个数 Optree hafman(int n,char m[],int w[]);//构造哈夫曼树，权值存在w[]中,返回树根 forest inforest(forest f,Optree t);//将每个二叉树连接起来.根据每个二叉树的根节点的权值大小,将二叉树权值由大到小相接 void shuxing(Optree p,int len);//输出树的形状，形参len=0; int bianma(Optree p,int a,char b[]);//对哈夫曼树进行编码,返回哈夫曼树的权值 int main(){ int a=0,d,k; char b[N+1],*p=NULL; char kkk[M]={""}; int type[3],*q=NULL;//type[0]=大写字母个数type[1]=小写字母个数type[2]=数字字符个数 Optree head; do{ printf("输入字符串<只录入字母或数字>(2--%d)字节:",N-1); d=gainchar(b,2,N); //d=b的字符长度 }while(jianyan(b,type)); //检验不合法时返回1 q=(int *)calloc(d,sizeof(int)); //申请 p=(char *)calloc(d+1,sizeof(char)); //申请 k=zhengli(b,p,q); //整理字符串 printf("大写字母:%d小写字母:%d数字:%d 共%d个字符 字符种类%d 种n注:X<<Y+<< X为出现的次数 Y为字符!n",type[0],type[1],type[2],d,k); head=hafman(k,p,q); //构造哈夫曼树 printf("①--②--③--④--⑤--⑥--⑦--⑧--⑨--⑩--①--②n"); shuxing(head,0); //显示树的形状 printf("总权值WPL=%d",bianma(head,0,kkk)); free(p); free(q); //此处可以改造一下bianma()函数让其释放哈夫曼树，我就不改了有时间再改 return 0; } Optree hafman(int n,char m[],int w[])//构造哈夫曼树，权值存在w[]中,返回树根 { forest p1,p2,froot; Optree leaves,t; froot=(forest)malloc(sizeof(Forest)); //建立一个根节点 froot->link=NULL; while(n-->0) //产生n个叶子 { leaves=(Optree)malloc(sizeof(Ptree)); //开辟新的叶子结点 leaves->w=w[n]; //给叶子结点赋权值 leaves->zha[0]=m[n]; //将字符存在叶子节点里 leaves->rchild=leaves->lchild=NULL; //叶子初始化 froot=inforest(froot,leaves); //按权值从大到小的顺序将叶子结点从froot树根向下排列，权值小的放在最后 } while(((froot->link)->link)!=NULL)//上面将叶子进行了初步排列，之后要对叶子进行合并,从树根开始两个两个的进行合并 { p1=froot->link; //p1指向第一片叶子 p2=p1->link; //p2指向第二片叶子 经过inforest函数排列后权值p1>=p2 froot->link=p2->link; //froot指向第三片叶子 t=(Optree)malloc(sizeof(Ptree)); //开辟新的结点 t->w=(p1->root->w)+(p2->root->w); //权相加 t->lchild=p1->root; //将叶子整合到t上 t->zha[0]='<'; t->rchild=p2->root; //产生新二叉树 froot=inforest(froot,t); //将新的二叉树t整合到树干上 free(p1); //释放p1所指的内存 free(p2); //释放p2 } t=froot->link->root;//当froot指向的最后一个节点link时此时的link节点已经是全部排列好的hafuman树 free(froot); //去掉froot留下树叉 return(t); //返回二叉树的树根 } forest inforest(forest f,Optree t)//将每个二叉树连接起来.根据每个二叉树的根节点的权值大小,将二叉树权值由大到小相接 { forest p=f->link,q=f,r; //q指向根,p指向根的下一个位置 r=(forest)malloc(sizeof(Forest)); //开辟新的树干结点 r->root=t; //将其叶子指针指向新加入的叶子t while (p!=NULL) //当整个树干没有到头时 { if(t->w > p->root->w) //如果t的权值大于ti的权值 { q=p; //q移到p的位置 p=p->link; //p向后寻找 } else p=NULL; //新插入的t<=某个位置的权，将在位置插入此节点，跳出while循环 } r->link=q->link; //r的下个节点指向q的后序节点 q->link=r; //r接在q的后面 return(f); //返回树根f } void shuxing(Optree p,int len)//输出树的形状，形参len=0; { int i,a,k=0; const char cha[4][6]={"<--+<","<+<","<<","<"}; if (p) { shuxing(p->rchild,len+1); //递归 for (i=1;i<=4*len;i++) printf("%c",i%4-1?' ':'|'); printf("%d<%c",p->w,p->zha[0]); //输出数据 a=p->w;k=0; while(a){ //求a的位数 a/=10; k++; } printf("%sn",cha[k]); shuxing(p->lchild,len+1); //递归 } } int gainchar(char *A,int min,int max)//长度在[min,max] <闭区间> 之间时 函数结束 返回字符串A的长度 { int B,C; do{ A[max]=B=C=0; while((A[B++]=getchar())!='n'&&B<max); if(A[B-1]!='n') while(getchar()!='n'&&++C); else A[--B]=0; if(C||B&&B<min) printf("您录入的字符串长度:%d字节n只录入(%d--%d)个字节!n",B+C,min,max); }while(C||B<min); return B; } int jianyan(char *ch,int type[3])//判断字符是否合法，合法返回1,不合法返回0 { const char a[3][3]={"AZ","az","09"};//对可能出现的字符进行判断 int b[2]={-1,0},i,j; type[0]=type[1]=type[2]=0; while(ch[++b[0]]);//求ch的长度 for(i=0;i<b[0];i++) { for(j=0;j<3;j++) if(ch[i]<=a[j][1]&&ch[i]>=a[j][0])//符合条件就加 { b[1]++; type[j]++; } if(!b[1])//不符合就返回 { printf("输入的字符中有除字母和数字以外的字符!n请重新"); return 1; } else b[1]=0;//否则 清楚标记 继续向下检验 } return 0; } int BF(char *a,char *b)//a为主串,b为被检验的串,d为匹配的下标 { int i=0,j=0,k=0; do{ if (b[j]&&a[i++]==b[j]) ++j; else { b[j]?(i-=j):k++; j=0; } }while(a[i-1]); return k; //返回b在a中的个数 } int zhengli(char b[],char *p,int *q) //对重复的进行整理 { int i,k,length=-1; char spot[2]={""}; while(b[++length]); for(i=0,k=0;i<length;i++) { spot[0]=b[i]; //每个字符串复制到spot中进行字符串匹配 if(!BF(p,spot)) //如果匹配失败，则说明此字符串第一次出现，就将其放在数组p里 { q[k]=BF(b,spot); p[k++]=spot[0]; } } return k; //返回不相同的总个数即 字符的种类 } int bianma(Optree p,int a,char b[]) //初始化a=c=0; { int static c=0; //设置静态变量c if(p) { if(p->lchild) //是左侧 { b[a]='0'; //左零右一 bianma(p->lchild,a+1,b); //继续遍历 } if(p->rchild) { b[a]='1'; //左零右一 bianma(p->rchild,a+1,b); //继续遍历 } if(p->zha[0]!='<') //如果是树叶 { b[a]=''; printf("%-13s"%c" %03d次n",b,p->zha[0],p->w); //输出编码和字符 c+=a*p->w; //计算权值 } } return c; //返回静态变量 即WPL }
最后
以上就是直率小白菜最近收集整理的关于哈夫曼编码的全部内容，更多相关哈夫曼编码内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。
发表评论 取消回复