一、数组介绍

数组是一种线性表，用连续的内存空间存储类型相同的数据元素。

像线性表、连续的内存空间都是什么意思呢？下面分别解释一下：

1、线性表

线性表的所有数据元素最多只有前和后两个方向的数据结构。

常见的线性表有数组、链表、队列、栈等。

非线性数据结构比较常见的是二叉树、图等。

2、连续的内存空间和类型相同的数据

在新建一个数组时，就会向内存申请一块连续的空间，这一块连续的空间会划分为相同大小的小块，在感觉上如下图所示：

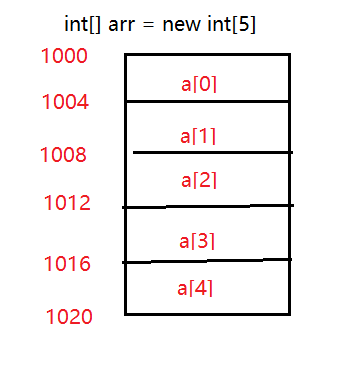
因为放的是 int 类型数据，所以每块所占的内存的大小都为 4 字节。

正式因为数组有连续的内存空间和类型相同的数据，所以才拥有它最突出的特性。它支持利用下标进行随机访问。

二、利用数组实现插入操作及相应的时间复杂度分析

1、数组原本有顺序，插入后需要继续保持数组有序

（1）思路分析

首先为了保证插入后数组还是有序，需要找到数组应该插入的位置 k 。

找到插入位置 k 后，需要将 k ~ n - 1 个数组元素都向后移一位，将 k 的位置空下来。

然后插入元素即可。

（2）代码实现

 /**
     * 有序插入 （顺序为从小到大）       平均时间复杂度为 O（n），最好时间复杂度为 O（1）,最坏时间复杂度为 O（n）
     *
     * @param e 被插入元素
     */
    public void addOrdered(int e) throws RuntimeException {
        // 判断是否已满，已满不能插入
        if (getSize() == getCapacity()) {
            throw new RuntimeException("当前数组元素已满，不能进行插入操作");
        }

        // 记录元素位置
        int k = -1;

        // 当前数组没有元素，直接插入
        if (getSize() == 0) {
            data[0] = e;
            setSize(getSize() + 1);
            return;
        }


        if (e < data[0]) {
            k = 0;
        } else if (e > data[getSize() - 1]){
            k = getSize();
        } else {
            // 遍历数组找到元素顺序
            for (k = 1; k < getSize(); k++) {
                if (e < data[k]) {
                    break;
                }
            }
        }


        // 将 k ~ n - 1 的数向后挪
        for (int i = getSize() - 1; i >= k; i--) {
            data[i + 1] = data[i];
        }

        // 将 e 插入 k 位置
        data[k] = e;
        // 元素个数加 1
        setSize(getSize() + 1);
    }

（3）时间复杂度分析

最好时间复杂度为 O(1)（当需要将元素插入在数组末尾时，不需要挪动其他的数组元素）

最坏时间复杂度为 O(n)（当需要将元素插入在数组头部时，需要挪动 n - 1 个数组元素）

平均时间复杂度为 O(n)（可能插入的位置的概率都是一样的，为 1/n，所以平均时间复杂度为 (1 + 2 + … n) / n = O(n)）

2、不需要保证数组的顺序，直接在数组末尾插入

（1）思路分析

由于不需要保证数组顺序，所以直接在数组末尾插入。

（2）代码实现

  /**
     * 插入元素到末尾 时间复杂度为 O（1）
     * @param e
     */
    public void add(int e) {
        // 判断是否已满，已满不能插入
        if (getSize() == getCapacity()) {
            throw new RuntimeException("当前数组元素已满，不能进行插入操作");
        }

        data[getSize()] = e;
        setSize(getSize() + 1);
    }

（3）时间复杂度分析

时间复杂度为 O（1）。

3、在数组指定位置插入

（1）思路分析

如果需要插入的位置为 k ，需要将 k ~ n - 1 个数组元素都向后移一位，将 k 的位置空下来。

然后插入元素即可。

（2）代码实现

 /**
     * 在指定位置插入
     *
     * @param index 下标，从 0 开始
     * @param e
     */
    public void add(int index, int e) {
        // 判断传入的下标是否合法
        if (index < 0 || index >= getCapacity()) {
            throw new RuntimeException("传入的数组下标不合法");
        }
        // 判断是否已满，已满不能插入
        if (getSize() == getCapacity()) {
            throw new RuntimeException("当前数组元素已满，不能进行插入操作");
        }

        if (size != 0) {
            if (index < getSize()) {
                for (int i = getSize(); i > index; i--) {
                    data[i] = data[i - 1];
                }
            }
        }
        data[index] = e;
        setSize(getSize() + 1);
    }

（3）时间复杂度分析

最好时间复杂度为 O（1）（当插入的位置是数组末尾时，或者数组没有数据时）。

最坏时间复杂度为 O（n）（插入的位置是数组首部时）。

平均时间复杂度为 O（n）（可能插入的位置的概率都是一样的，为 1/n，所以平均时间复杂度为 (1 + 2 + … n) / n = O(n)）。

三、利用数组实现删除操作及相应的时间复杂度分析

1、直接删除指定下标的元素

（1）思路分析

将 k + 1 ~ 到 n -1 位置的元素向前移一位，覆盖掉删除的元素即可。

（2）代码实现

 /**
     * 删除（需要保证数据连续性）
     *
     * @param k 被删除元素的位置 （该位置从 0 开始）
     * @return 被删除元素
     */
    public int del(int k) throws RuntimeException {
        // 判断 k 的合法性
        if (k < 0 || k >= getSize()) {
            throw new RuntimeException("给定的元素位置不合法");
        }
        // 保存 k 位置的数据
        int e = data[k];
        // 将 k + 1 后的元素向前移动，覆盖 k 位置的元素，保持数组数据的连续性
        for (int i = k + 1; i < getSize(); i++) {
            data[i - 1] = data[i];
        }
        // 修改数组元素个数
        setSize(getSize() - 1);
        // 返回被删除元素
        return e;
    }

（3）时间复杂度分析

删除操作的时间复杂度的计算方式和插入类似。

最好时间复杂度是 O（1）（当删除的元素为数组末尾元素时，不需要移动数组元素）。

最坏时间复杂度是 O（n）（当删除的元素为数组头部元素时，需要将 1 ~ n-1 的元素向前移动）。

平均时间复杂度是 O（n）（需要删除的数据元素的插入的位置的概率都是一样的，为 1/n，所以平均时间复杂度为 (1 + 2 + … n) / n = O(n)）

四、完整代码

package demo.array;

import java.util.Arrays;

/**
 * @author liyanan
 * @date 2019/12/25 15:02
 */
public class ArrayList {
    private int[] data;

    private int size;

    private int capacity;

    public ArrayList(int capacity) {
        this.capacity = capacity;
        size = 0;
        data = new int[capacity];
    }

    public int getSize() {
        return size;
    }

    public int getCapacity() {
        return capacity;
    }

    public void setSize(int size) {
        this.size = size;
    }

    /**
     * 有序插入 （顺序为从小到大）       平均时间复杂度为 O（n），最好时间复杂度为 O（1）,最坏时间复杂度为 O（n）
     *
     * @param e 被插入元素
     */
    public void addOrdered(int e) throws RuntimeException {
        // 判断是否已满，已满不能插入
        if (getSize() == getCapacity()) {
            throw new RuntimeException("当前数组元素已满，不能进行插入操作");
        }

        // 记录元素位置
        int k = -1;

        // 当前数组没有元素，直接插入
        if (getSize() == 0) {
            data[0] = e;
            setSize(getSize() + 1);
            return;
        }


        if (e < data[0]) {
            k = 0;
        } else if (e > data[getSize() - 1]) {
            k = getSize();
        } else {
            // 遍历数组找到元素顺序
            for (k = 1; k < getSize(); k++) {
                if (e < data[k]) {
                    break;
                }
            }
        }


        // 将 k ~ n - 1 的数向后挪
        for (int i = getSize() - 1; i >= k; i--) {
            data[i + 1] = data[i];
        }

        // 将 e 插入 k 位置
        data[k] = e;
        // 元素个数加 1
        setSize(getSize() + 1);
    }

    public String printArrayList() {
        StringBuilder sb = new StringBuilder();
        sb.append("array = [");
        for (int i = 0; i < getSize(); i++) {
            sb.append(data[i]);
            if (i < getSize() - 1) {
                sb.append(", ");
            }
        }
        sb.append("]");
        sb.append(", size = ");
        sb.append(getSize());
        sb.append(", capacity = ");
        sb.append(getCapacity());
        return sb.toString();
    }

    /**
     * 插入元素到末尾 时间复杂度为 O（1）
     *
     * @param e
     */
    public void add(int e) {
        // 判断是否已满，已满不能插入
        if (getSize() == getCapacity()) {
            throw new RuntimeException("当前数组元素已满，不能进行插入操作");
        }

        data[getSize()] = e;
        setSize(getSize() + 1);
    }

    /**
     * 在指定位置插入
     *
     * @param index 下标，从 0 开始
     * @param e
     */
    public void add(int index, int e) {
        // 判断传入的下标是否合法
        if (index < 0 || index >= getCapacity()) {
            throw new RuntimeException("传入的数组下标不合法");
        }
        // 判断是否已满，已满不能插入
        if (getSize() == getCapacity()) {
            throw new RuntimeException("当前数组元素已满，不能进行插入操作");
        }

        if (size != 0) {
            if (index < getSize()) {
                for (int i = getSize(); i > index; i--) {
                    data[i] = data[i - 1];
                }
            }
        }
        data[index] = e;
        setSize(getSize() + 1);
    }

    /**
     * 删除（需要保证数据连续性）
     *
     * @param k 被删除元素的位置 （该位置从 0 开始）
     * @return 被删除元素
     */
    public int del(int k) throws RuntimeException {
        // 判断 k 的合法性
        if (k < 0 || k >= getSize()) {
            throw new RuntimeException("给定的元素位置不合法");
        }
        // 保存 k 位置的数据
        int e = data[k];
        // 将 k + 1 后的元素向前移动，覆盖 k 位置的元素，保持数组数据的连续性
        for (int i = k + 1; i < getSize(); i++) {
            data[i - 1] = data[i];
        }
        // 修改数组元素个数
        setSize(getSize() - 1);
        // 返回被删除元素
        return e;
    }
}

最后

以上就是热情钢笔为你收集整理的数据结构与算法学习（一）：线性表之数组的插入与删除（Java 实现）一、数组介绍二、利用数组实现插入操作及相应的时间复杂度分析三、利用数组实现删除操作及相应的时间复杂度分析四、完整代码的全部内容，希望文章能够帮你解决数据结构与算法学习（一）：线性表之数组的插入与删除（Java 实现）一、数组介绍二、利用数组实现插入操作及相应的时间复杂度分析三、利用数组实现删除操作及相应的时间复杂度分析四、完整代码所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。