线性表综合讲解（思想、实现）一、顺序表二、链表三、栈四、队列

74 阅读 0 评论 49 点赞

我是靠谱客的博主深情盼望，最近开发中收集的这篇文章主要介绍线性表综合讲解（思想、实现）一、顺序表二、链表三、栈四、队列，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

线性表中的数据都像是被串起来一样，具有单一线性关系

一、顺序表

（一）非动态版本

（二）动态版本

二、链表

（一）单链表

(二)双向链表

(三)静态链表

(四)循环链表

三、栈

(一)顺序栈

(二)两栈

(三)链栈

四、队列

线性表中的数据都像是被串起来一样，具有单一线性关系

一、顺序表

思想：在内存中数据连续存储

这就是一块连续存储的数据。

（一）非动态版本

#define MAX_CAPACITY 100  //定义存储上限
#include<stdio.h>
#include<stdlib.h>
typedef struct Sequencechart
{
	int p[MAX_CAPACITY]; //创建一个数组存储数据
	int sz; //表示已存数量
}S;

void Initchart(S*pf)
{
	pf->p[MAX_CAPACITY] = 0; //存储数据初始化为0
	pf->sz = 0; //存储数量为0
}
int checkcapacity(S*pf)
{
	if (pf->sz == MAX_CAPACITY)  //检查是否超过上限
		return 0;
	else
		return 1;
}
void Add(S*pf, int n)
{
	checkcapacity(pf);
	pf->p[pf->sz] = n; //sz可作为下标
	pf->sz++;
}
int Delete(S*pf, int n)
{
	if (!pf->sz) //顺序表为空，返回0
		return 0;
	for (int i = n - 1; i < pf->sz - 1; i++)  //删除某个数据后，要将后面的数向前移动
		pf->p[i] = pf->p[i + 1];
	pf->sz--;
	return 1;
}
int Check(S*pf, int n)
{
	if (!pf->sz)
		return 0;
	for (int i = 0; i < pf->sz; i++)
	{
		if (n == pf->p[i])
		{
			printf("找到了，下标为%dn", i); //查找某数据是否存在。
		}
	}
	return 1;
}
int Modify(S*pf, int n, int ps) //传入修改数据，下标
{
	if (!pf->sz)
		return 0;
	if (ps > pf->sz)
		return -1;
	pf->p[ps] = n;
	return 1;
}
int main()
{
	S s;
	Initchart(&s);
	for (int i = 0; i < 9; i++)
		Add(&s, i + 1);
	for (int i = 0; i < s.sz; i++)
		printf("%d ", s.p[i]);
	printf("n");
	Delete(&s, 5);
	for (int i = 0; i < s.sz; i++)
		printf("%d ", s.p[i]);
	printf("n");
	Modify(&s, 777, 2);
	for (int i = 0; i < s.sz; i++)
		printf("%d ", s.p[i]);
	printf("n");
	Check(&s, 777);
	return 0;
}

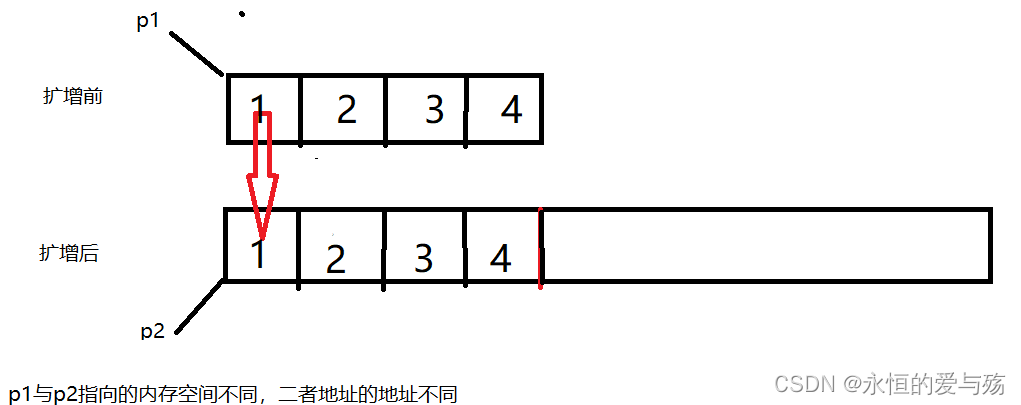
（二）动态版本

注：当初始空间不足以扩增至所需时，realloc会重新选择一块空间并将原数据拷贝过来

#define INITCAPACITY 3 //初始容量
#define ADDNUM 2   //每次扩增的大小
#include<stdio.h>
#include<stdlib.h>
typedef struct Sequencechart
{
    int*p; //用指针指向内存空间
	int capacity; //当前容量大小
	int sz;
}S;

int Initchart(S*pf)
{
	pf->capacity = INITCAPACITY;
	pf->p = malloc(sizeof(int)*(pf->capacity)); //初始开辟空间
	pf->sz = 0;
	return 1;
}
int checkcapacity(S*pf)
{
	if (pf->sz == pf->capacity) //达到当前容量后扩增
	{
		pf->capacity += ADDNUM;
		pf->p= realloc(pf->p, sizeof(int)*pf->capacity); //realloc第一个参数为指向待扩增空间的指针，即地址，第二个为扩增后的大小，为字节数。
	}
	return 1;
}
int Add(S*pf, int n)
{
	checkcapacity(pf);
	pf->p[pf->sz] = n;
	pf->sz++;
	return 1;
}
int Delete(S*pf, int n)
{
	if (!pf->sz)
		return 0;
	for (int i = n - 1; i < pf->sz - 1; i++)
		pf->p[i] = pf->p[i + 1];
	pf->sz--;
	return 1;
}
int Check(S*pf, int n)
{
	if (!pf->sz)
		return 0;
	for (int i = 0; i < pf->sz; i++)
	{
		if (n == pf->p[i])
		{
			printf("找到了，下标为%dn", i);
		}
	}
	return 1;
}
int Modify(S*pf, int n,int ps)
{
	if (!pf->sz)
		return 0;
	if (ps > pf->sz)
		return -1;
	pf->p[ps] = n;
	return 1;
}
int main()
 {
	S s;
	Initchart(&s);
	for (int i = 0; i < 9; i++)
		Add(&s, i + 1);
	for (int i = 0; i <s.sz; i++)
		printf("%d ", s.p[i]);
	printf("n");
	Delete(&s, 5);
	for (int i = 0; i < s.sz; i++)
		printf("%d ", s.p[i]);
	printf("n");
	Modify(&s, 777, 2);
	for (int i = 0; i < s.sz; i++)
		printf("%d ", s.p[i]);
	printf("n");
	Check(&s, 777);
	free(s.p);
	return 0;
}

学会了基本的顺序表后就可以写通讯录这样的小程序了。

二、链表

思想：在内存中数据可以不连续存储，用指针寻找下一个或上一个元素

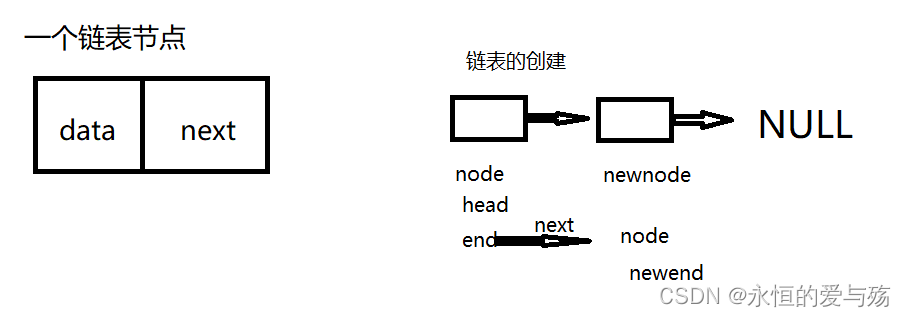
L*SetLinkList(int n) //创建链表
{
	L*head = NULL, *end = NULL;
	for (int i = 0; i < n; i++)
	{
		L*node = (L*)malloc(sizeof(L));
		node->data = i;
		node->next = NULL;
		if (!head)
			head =end= node;
		else
		{
			end->next = node;
			end = node;
		}
	}
	return head;
}

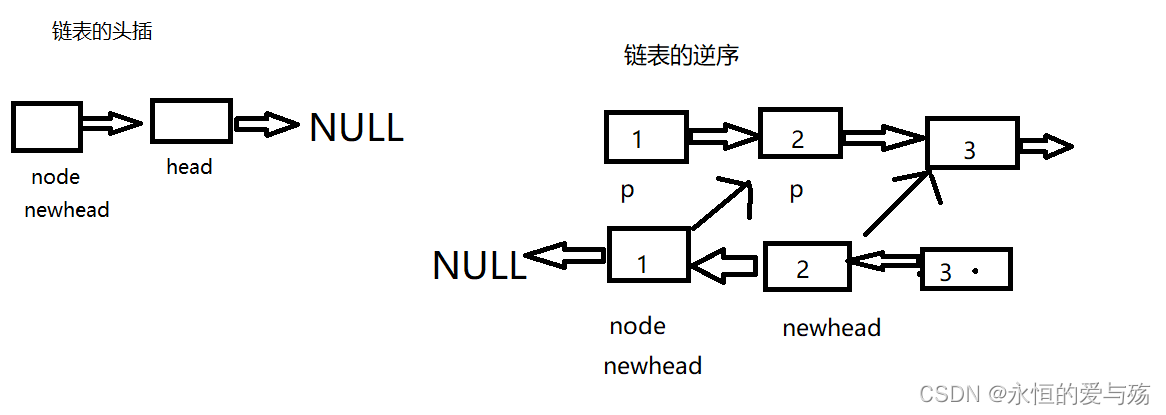
void Headinsert(L*p, int val) //头插数据
{
	L*node = (L*)malloc(sizeof(L));
	node->data = val;
	node->next = p;
	p = node;
}  

L*Reverse(L*p) //翻转链表
{
	L*newhead = NULL, *node = NULL;
	while (p)
	{
		node = p;
		p = p->next;
		node->next = newhead;
		newhead = node;
	}
	return newhead;
}

（一）单链表

#pragma once
#include<stdio.h>
#include<stdlib.h>
typedef struct LinkList
{
	int data;
	struct LinkList*next;
}L;
L*SetLinkList(int n) //创建链表
{
	L*head = NULL, *end = NULL;
	for (int i = 0; i < n; i++)
	{
		L*node = (L*)malloc(sizeof(L));
		node->data = i;
		node->next = NULL;
		if (!head)
			head =end= node;
		else
		{
			end->next = node;
			end = node;
		}
	}
	return head;
}
L*Addnode(L*p, int val, int n)
{
	L*prev = p;
	L*cur = p;
	while (n--)
	{
		prev = cur;
		cur = cur->next;
	}
	L*node = (L*)malloc(sizeof(L));
	node->data = val;
	prev->next = node;
	node->next = cur;
	return p;
}
void*Headinsert(L*p, int val) //头插数据
{
	L*node = (L*)malloc(sizeof(L));
	node->data = val;
	node->next = p;
	p = node;
}  
L*Delete_fdata(L*p, int val)//数据查找
{
	if (p->data == val)
	{
		p = p->next;
		return p;
	}
	L*prev = p;
	L*cur = p;
	while (cur->data != val)
	{
		prev = cur;
		cur = cur->next;
	}
	prev->next = cur->next;
	free(cur);
	cur = NULL;
	return p;
}
L*Delete_index(L*p, int n)//下标查找
{
	if (n == 1)
	{
		p = p->next;
		return p;
	}
	L*prev = p;
	L*cur = p;
	while (n--)
	{
		if (!cur)
		{
			prev->next = NULL;
			return p;
		}
		prev = cur;
		cur = cur->next;
	}
	prev->next = cur->next;
	free(cur);   //开辟的内存空间一定要释放，防止内存泄漏
	cur = NULL;
	return p;

}
int Find_fdata(L*p, int val)//数据查找
{
	L*cur = p;
	int index = 0;
	while (cur->data != val)
	{
		cur = cur->next;
		index++;
	}
	return index;
}
L*Find_index(L*p, int n)//下标查找
{
	L*cur = p;
	while (n--)
	{
		cur = cur->next;
	}
	return cur;
}
L*Modify(L*p, int val, int n)
{
	L*cur = p;
	Find_index(p, n)->data = val;
	return p;
}
L*Reverse(L*p) //翻转链表
{
	L*newhead = NULL, *node = NULL;
	while (p)
	{
		node = p;
		p = p->next;
		node->next = newhead;
		newhead = node;
	}
	return newhead;
}

(二)双向链表

在单链表的基础上增加了一个指向前一个数据的指针

#pragma once
#include<stdio.h>
#include<stdlib.h>

typedef struct LinkList
{
	int data;
	struct LinkList*prev;
	struct LinkList*next;
}L;
L*SetLinkList(int n)
{
	L*head = NULL, *end = NULL;
	for (int i = 0; i < n; i++)
	{
		L*node = (L*)malloc(sizeof(L));
		node->data = i;
		node->prev = node->next = NULL;
		if (!head)
			head = end = node;
		else
		{
			node->prev = end;  //让prev指针指向上一次的end
			end->next = node;
			end = node;
		}
	}
	return head;
}
L*Search(L*p, int index)
{
	L*cur = p;
	while (index--)
	{
		cur = cur->next;
	}
	return cur;
}
L*Headadd(L*p,int val) //头插节点
{
	L*node = (L*)malloc(sizeof(L));
	node->data = val;
	node->next = p;
	p->prev = node;
	node->prev = NULL;
	return node;
}
void Add(L*p, int index,int val)
{
	L*cur = Search(p, index);
	L*node = (L*)malloc(sizeof(L));
	node->data = val;
	node->next = cur->next;
	cur->next->prev = node;
	cur->next = node;
	node->prev = cur;
}
void Delete(L*p, int index)
{
	L*cur = p;
	while (index--)
	{
		cur = cur->next;
	}
	cur->prev->next = cur->next; //删除时也要注意prev指针
	cur->next->prev = cur->prev;
	free(cur);
    cur=NULL;
}
void Modify(L*p,int val,int index)
{
	L*cur = Search(p, index);
	cur->data = val;
}

双向链表就不用费劲逆序了

(三)静态链表

静态链表采用结构体数组模拟链表，其index游标相当于next指针，一个记录下一个数据的下标，另一个则存储地址

相较于数组，删除添加数据时只需修改游标，无需移动数据，但使用的是连续空间，不具备链表随机存取的特点

//静态链表
#include<stdio.h>
#define MAX_SIZE 1000
#define ERROR -1
#define OK 1
typedef int ElemType;
typedef int Status;
typedef struct
{
	ElemType data;
	int index;
}S_list, Static_LinkList[MAX_SIZE];
Status InitList(S_list*sl)
{
	for (int i = 0; i < MAX_SIZE - 1; i++)
		sl[i].index = i + 1;
	sl[MAX_SIZE - 1].index = 0;
	return OK;
}
int Malloc_sl(S_list*s)
{
	int tmp = s[0].index;//使用备用元素,存储的为空闲位置的下标
	if (tmp)
		s[0].index = s[tmp].index;//更新备用元素
	return tmp;
}
int ListLength(S_list*s)
{
	int cnt = 0;
	int i = s[MAX_SIZE - 1].index;
	while (i)
	{
		i = s[i].index;
		cnt++;
	}
	return cnt;
}
Status ListInsert(S_list*s,int num,ElemType e)
{
	int j, k;
	k = MAX_SIZE - 1;
	if (num<1 || num>ListLength(s)+1)
		return ERROR;
	j = Malloc_sl(s);
	if (j)
	{
		s[j].data = e;
		for (int l = 1; l < num; l++)
			k = s[k].index;
		s[j].index = s[k].index;
		s[k].index = j;
		return OK;
	}
	return ERROR;
}

void Free_sl(S_list*s, int k)
{
	s[k].index = s[0].index;
	s[0].index = k;
}

Status ListDelete(S_list*s, int num)
{
	int j, k;
	if (num<1 || num>ListLength(s))
		return ERROR;
	k = MAX_SIZE - 1;
	for (int j = 1; j < num; j++)
		k = s[k].index;
	j = s[k].index;
	s[k].index = s[j].index;
	Free_sl(s,j);
	return OK;
}

void ShowList(S_list*s, int l, int r)
{
	for (int i = l; i <r; i++)
		printf("%d %dn", s[i].data, s[i].index);
}
int main()
{
	Static_LinkList sl;
	InitList(sl);
	for (int i = 1; i < 500; i++)
		ListInsert(sl, i, i);
	ShowList(sl, 0, 500);
	printf("%dn", ListLength(sl));
	for (int i = 0; i < 250; i++)
		ListDelete(sl, i);
	ShowList(sl, 0, 250);
	printf("%dn", ListLength(sl));
	return 0;
}

(四)循环链表

在单链表的基础上，让尾节点指向头部即可

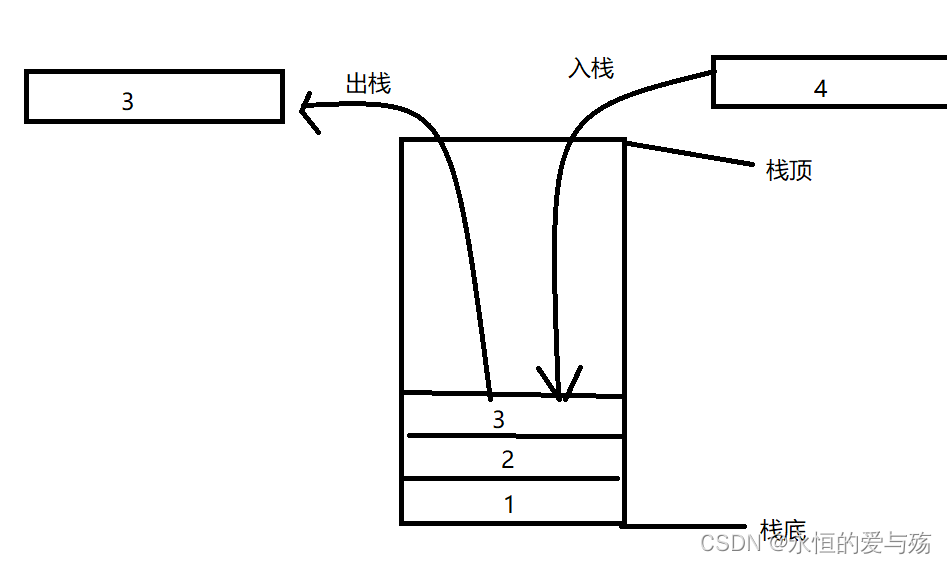
三、栈

思想：先入的数据放在栈底，后入的放在栈顶，遵循先入后出，即FILO（first in last out）

(一)顺序栈

#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>

#define INITCAPACITY 10  //栈的初始容量

typedef int STD;   //为数据类型起一个别名，代表栈的数据

typedef struct Stack
{
	STD*base; //栈底为指向内存空间的指针
	STD top; //栈顶可代表下标，这里用数组实现栈，当然还有别的方法
	int capacity; //栈的当前容量
}S;

void InitStack(S*pf)
{
	pf->base =(int*)malloc(sizeof(int)*INITCAPACITY); //初始空间
	pf->capacity = INITCAPACITY;
	pf->top = 0;
}
void checkcapacity(S*pf)
{
	assert(pf); //pf为空断言报错，便于查找错误
	if (pf->top == pf->capacity)
	{
		pf->capacity *= 2; //不够增容为原来的两倍
		pf->base =(STD*)realloc(pf->base,pf->capacity*sizeof(int));
	}
}
//入栈
void StackPush(S*pf, int n)
{
	checkcapacity(pf);
	pf->base[pf->top] = n;
	pf->top++;
}
//出栈
void StackPop(S*pf)
{
	assert(pf&&pf->top > 0);
	pf->top--; //不必释放空间，再次赋值即可重新利用
}
//判断是否为空栈
bool StackEmpty(S*pf)
{
	assert(pf);
	if (pf->top == 0)
		return true;
	else
		return false;
}
//释放栈
void StackDestory(S*pf)
{
	assert(pf);
	pf->capacity = pf->top = 0;
	free(pf->base);
	pf->base = NULL;
}
//获取栈顶元素
int StackTop(S*pf)
{
	assert(pf&&pf->top > 0); //栈顶要大于0才有数据
	return pf->base[pf->top - 1];
}
//获取栈内的数据数量
int StackSize(S*pf)
{
	assert(pf);
	return pf->top;
}

(二)两栈

将一个数组分为两个栈，从两边向中间存储

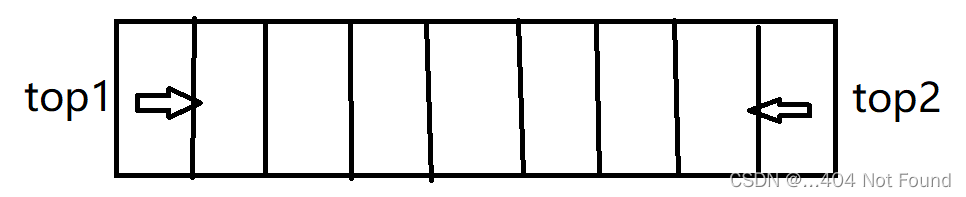
当栈一存值,top1++，栈二存值，top2--，当top1+1==top2时,两站则已存满。

两栈共享一块空间

//双栈
#include<stdio.h>
#include<stdlib.h>
#define MAX_SIZE 100
typedef int ElemType;
typedef struct
{
	ElemType data[MAX_SIZE];
	int top1;
	int top2;
}stack;
void InitStack(stack*s)
{
	s->top1 = 0;
	s->top2 = MAX_SIZE;
}
void push(stack*s,ElemType e,int stacknum)
{
	if (s->top1 + 1 == s->top2)
		return;
	if (stacknum == 1)
		s->data[++s->top1] = e;
	if (stacknum == -1)
		s->data[--s->top2] = e;
}
void pop(stack*s, int stacknum,ElemType*back)
{
	if (stacknum == 1)
	{
		if (s->top1 == -1)
			return;
		else
			*back=s->data[s->top1--];
	}
	if (stacknum == -1)
	{
		if (s->top2 == MAX_SIZE)
			return;
		else
			*back=s->data[s->top2++];
	}
}
int main()
{
	stack s;
	InitStack(&s);
	int flag = 1;
	for (int i = 0; i < 100; i++,flag*=-1)
		push(&s, i, flag);
	int*num=(int*)malloc(sizeof(int));
	for (int i = 0; i < 100; i++,flag*=-1)
	{
		pop(&s, flag, num);
		printf("%d ", *num);
	}
	free(num);
	num = NULL;
	return 0;
}

(三)链栈

使用链表存储数据，采用头插push值

//链栈
#include<stdio.h>
#include<stdlib.h>
typedef int ElemType;
typedef struct LinkNode
{
	ElemType*data;
	struct LinkNode*next;
}Node;
typedef struct
{
	Node*top;
	int size;
}LinkStack;
void InitStack(LinkStack*ls)
{
	ls->size = 0;
	ls->top = NULL;
}
void push(LinkStack*ls, ElemType e)
{
	Node*node = (Node*)malloc(sizeof(Node));
	node->data = e;
	node->next = ls->top;
	ls->top = node;
	ls->size++;
}
void pop(LinkStack*ls, ElemType*back)
{
	if (ls->size == 0)
		return;
	*back = ls->top->data;
	Node*p = ls->top;
	ls->top = ls->top->next;
	free(p);
	p = NULL;
	ls->size--;
}
int main()
{
	LinkStack s;
	ElemType*num = (ElemType*)malloc(sizeof(ElemType));
	InitStack(&s);
	for (int i = 0; i < 100; i++)
		push(&s, i);
	for (int i = 0; i < 100; i++) {
		pop(&s, num);
		printf("%d ", *num);
	}
	free(num);
	num = NULL;
}

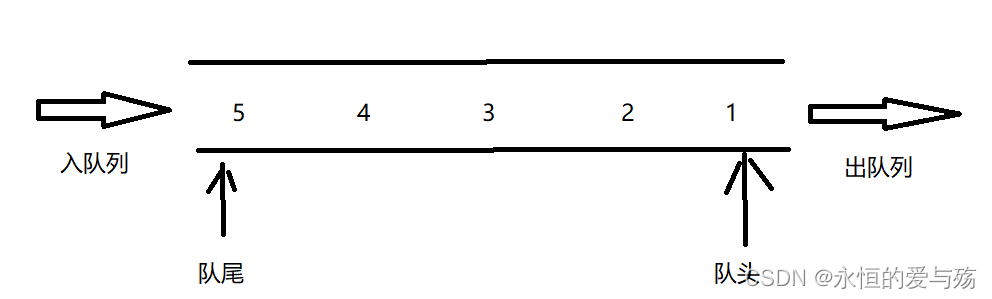
四、队列

思想：先入先出，像通过走廊一样

#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>
#include<assert.h>

typedef	int QUD;

typedef struct QueueNode //这里用链表实现队列
{
	struct QueueNode*next;
	QUD data;
}Qnode;
typedef struct Queue
{
	Qnode*head;
	Qnode*tail;
}Queue;
void QueueInit(Queue*p)
{
	assert(p);
	p->head = p->tail = NULL;
}
//入队列
void QueuePush(Queue*p, QUD n)
{
	assert(p);
	Qnode*node = (Qnode*)malloc(sizeof(Qnode));
	node->next = NULL;
	node->data = n;
	if (p->tail == NULL)
	{
		p->head = p->tail = node;
	}
	else
	{
		p->tail->next = node; //用队尾入数据
		p->tail = node;
	}
}
出队列
void QueuePop(Queue*p)
{
	assert(p&&p->head);
	if (p->head->next == NULL) //只有一个节点直接free头
	{
		free(p->head);
		p->head = p->tail = NULL;
	}
	else
	{
		Qnode*temp = p->head->next; //将下一节点设为头并释放原头内存
		free(p->head);
		p->head = temp;
	}
}
//取队头元素
QUD QueueFront(Queue*p)
{
	assert(p&&p->head);
	return p->head->data;
}
QUD QueueBack(Queue*p)
{
	assert(p&&p->head);
	return p->tail->data;
}
//释放队列
void QueueDestory(Queue*p)
{
	assert(p);
	Qnode*cur = p->head;
	while (cur)
	{
		Qnode*temp = cur->next;
		free(cur);
		cur = temp;
	}
	p->head = p->tail = NULL;
}
//判断队列是否为空
bool QueueEmpty(Queue*p)
{
	return p->head == NULL;
}
//获取队列中元素的个数
int QueueSize(Queue*p)
{
	assert(p);
	int size = 0;
	Qnode*cur = p->head;
	while (cur)
	{
		size++;
		cur = cur->next;
	}
	return size;
}

这里都用了最简单的办法实现栈和队列，先把这四种数据结构的逻辑思想搞懂，再去深入了解其用法和不同的实现方式。

最后

以上就是深情盼望为你收集整理的线性表综合讲解（思想、实现）一、顺序表二、链表三、栈四、队列的全部内容，希望文章能够帮你解决线性表综合讲解（思想、实现）一、顺序表二、链表三、栈四、队列所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。

本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。

本文分类：数据结构
浏览次数：74 次浏览
发布日期：2023-09-23 23:55:53
本文链接：https://www.kaopuke.com/article/k-p-k_14_uzocfx_13_z_10_y.html

线性表综合讲解（思想、实现）一、顺序表二、链表三、栈四、队列

概述

线性表中的数据都像是被串起来一样，具有单一线性关系

一、顺序表

（一）非动态版本

（二）动态版本

二、链表

（一）单链表

(二)双向链表

(三)静态链表

(四)循环链表

三、栈

(一)顺序栈

(二)两栈

(三)链栈

四、队列

最后

评论列表共有 0 条评论

发表评论取消回复

线性表综合讲解（思想、实现）一、顺序表二、链表三、栈四、队列

概述

线性表中的数据都像是被串起来一样，具有单一线性关系

一、顺序表

（一）非动态版本

（二）动态版本

二、链表

（一）单链表

(二)双向链表

(三)静态链表

(四)循环链表

三、栈

(一)顺序栈

(二)两栈

(三)链栈

四、队列

最后

相关文章

评论列表共有 0 条评论

发表评论 取消回复

发表评论取消回复