目录
一、顺序查找法
1.1 算法实现
1.1.1 算法一:设置监视哨的顺序查找法
1.1.2 算法二:不设置监视哨的顺序查找法
1.2 算法性能分析
二、折半查找法
2.1 算法实现
2.3 算法性能分析
基于线性表的查找法具体可分为顺序查找法、折半查找法、分块查找法。
一、顺序查找法
基本思想:用所给关键字与线性表中各元素的关键字逐个比较,直到成功或失败。
存储结构通常为顺序结构,也可为链式结构。这里采用的是顺序结构。
#define LIST_SIZE 20
typedef struct {
KeyType key;
OtherType other_data;
} RecordType;
typedef struct {
RecordType r[LIST_SIZE+1]; /* 保留r[0]为工作单元 */
int length;
} RecordList;
1.1 算法实现
1.1.1 算法一:设置监视哨的顺序查找法
算法思想:在表的一端设置一个称为“监视哨”的附加单元,存放要查找元素的关键字。从表的另一端开始查找。如果在表中找到要查找的元素,则返回对应的下标;否则意味着在监视哨位置找到该元素,返回下标0,代表查找失败。
int SeqSearch(RecordList L, KeyType k) {
L.r[0] = k;
int i = L.length;
while (L.r[i].key != k) --i;
return i;
}1.1.2 算法二:不设置监视哨的顺序查找法
int SeqSearch(RecordList L, KeyType k) {
int i = L.length;
while (i >= 1 && L.r[i].key != k) --i;
return i;
}算法二与算法一相比,循环控制条件中增加了i>=1,用以判断查找过程是否越界。加设监视哨可省去这个条件,从而提高查找效率。
1.2 算法性能分析

二、折半查找法
折半查找法对要查找的列表有两个要求:
- 必须采用顺序存储结构
- 必须按关键字大小有序排列
2.1 算法实现
算法思想:
- 首先取表中间记录的关键字与待查找关键字作比较。如果两者相等,则查找成功;否则,以中间位置为准将表分为左、右两个半区。
- 如果该记录的关键字大于待查找关键字,则进一步查找左半区;否则,进一步查找右半区。
- 重复1、2,直到查找成功,或所查找的区域无记录,查找失败。
int BinSearch(RecordList L, KeyType k) {
low = 0;
high = L.length - 1;
while (low <= high) {
mid = (low + high) / 2;
if (L.r[mid].key == k) return mid;
else if (L.r[mid].key > k) high = mid - 1;
else low = mid + 1;
}
return 0;
}注意:根据具体的数组存储情况设置low和high的值。
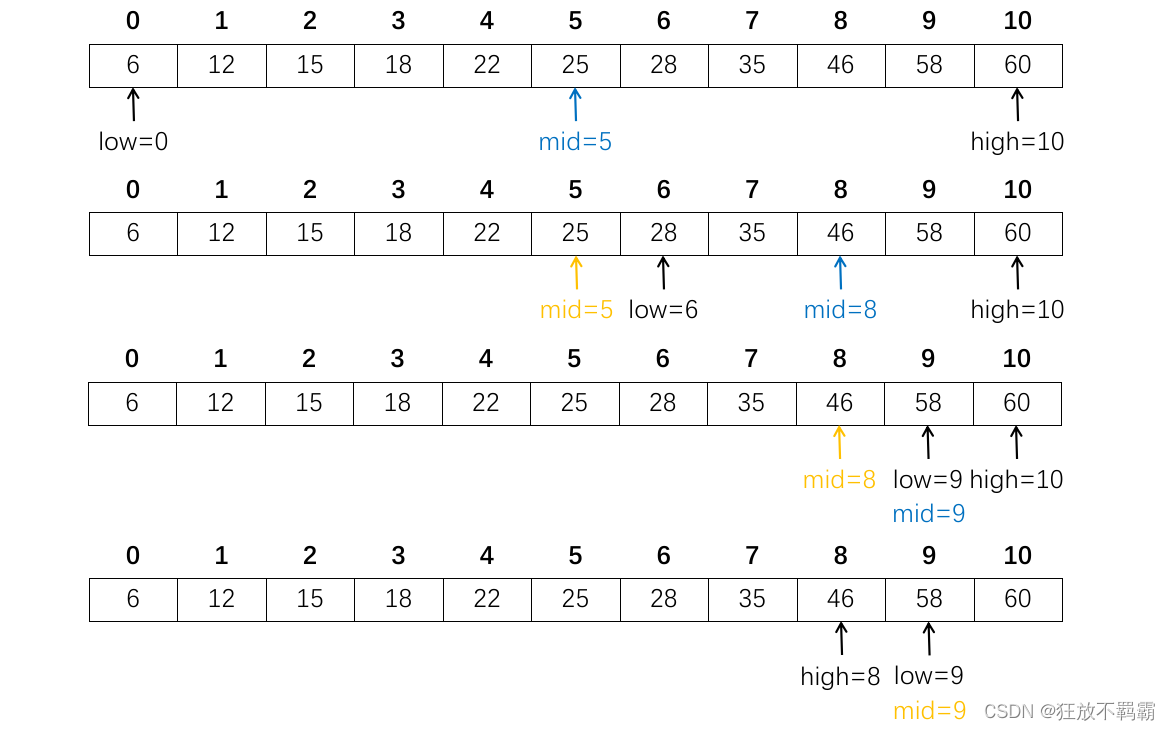
为方便理解,给出一个使用折半查找法的例子(查找关键字50,最终查找失败)。
为方便观察,蓝色标明当前循环中mid的值,黄色标明上一轮循环中mid的值。
2.3 算法性能分析
根据折半查找法,画出上述例子的查找过程。
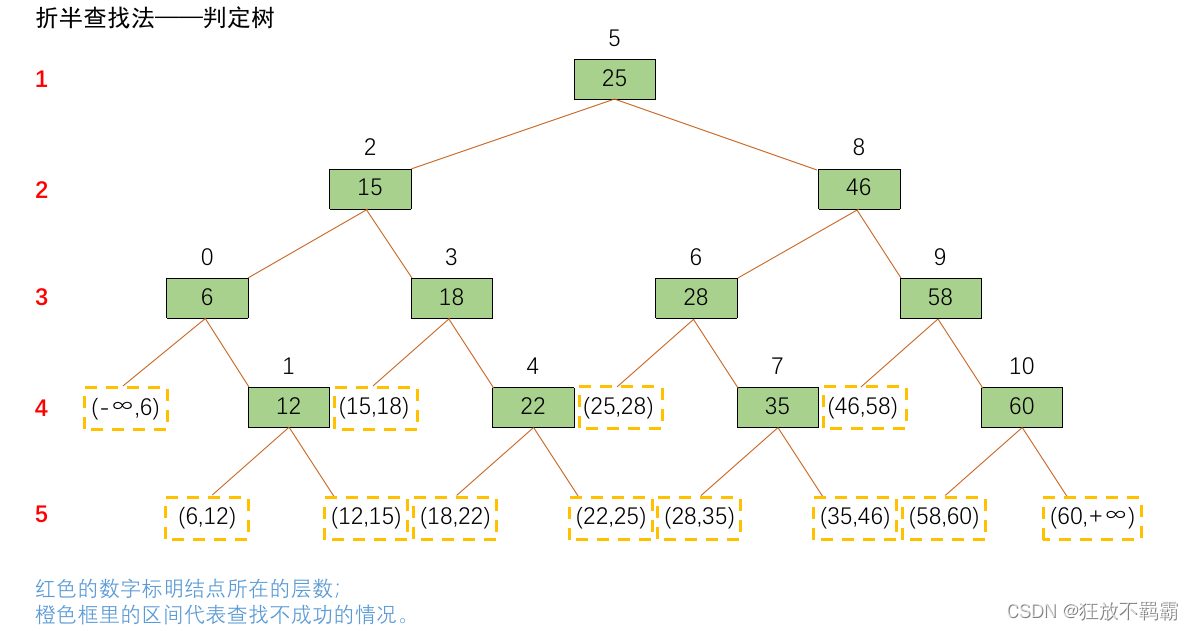
根据分析,可以得出以下结论。
查找成功: 比较次数 = 路径上的结点数 = 结点的层数
查找失败: 比较次数 = 路径上的结点数(即绿色结点的数目)
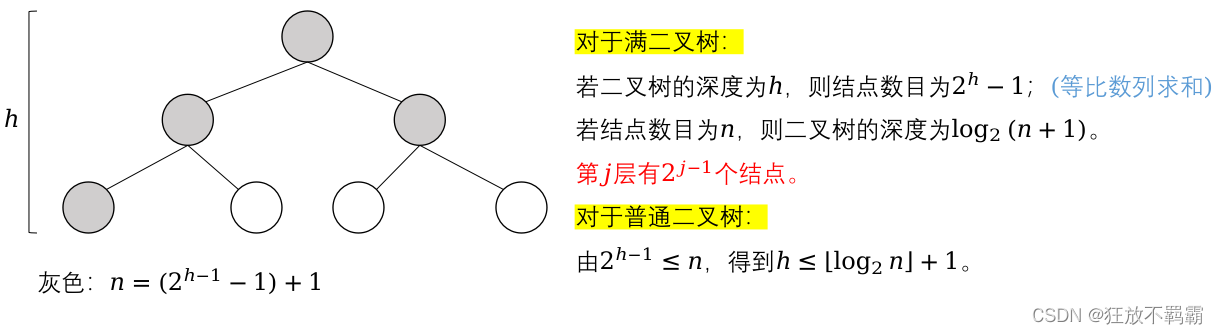
再结合二叉树的性质,计算出平均查找长度(假设判定树是一个满二叉树)。

回顾:二叉树的性质。
最后
以上就是单薄月饼最近收集整理的关于查找——基于线性表的查找法一、顺序查找法二、折半查找法的全部内容,更多相关查找——基于线性表内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供,作为学习参考使用,或来自网络收集整理,版权属于原作者所有。








发表评论 取消回复