概述
Keywords: Dfs, 思维
In the big cities, the subway systems always look so complex to the visitors. To give you some sense, the following figure shows the map of Beijing subway. Now you are supposed to help people with your computer skills! Given the starting position of your user, your task is to find the quickest way to his/her destination.
Input Specification:
Each input file contains one test case. For each case, the first line contains a positive integer N (≤ 100), the number of subway lines. Then N lines follow, with the i-th (i=1,⋯,N) line describes the i-th subway line in the format:
M S[1] S[2] … S[M]
where M (≤ 100) is the number of stops, and S[i]'s (i=1,⋯,M) are the indices of the stations (the indices are 4-digit numbers from 0000 to 9999) along the line. It is guaranteed that the stations are given in the correct order – that is, the train travels between S[i] and S[i+1] (i=1,⋯,M−1) without any stop.
Note: It is possible to have loops, but not self-loop (no train starts from S and stops at S without passing through another station). Each station interval belongs to a unique subway line. Although the lines may cross each other at some stations (so called “transfer stations”), no station can be the conjunction of more than 5 lines.
After the description of the subway, another positive integer K (≤ 10) is given. Then K lines follow, each gives a query from your user: the two indices as the starting station and the destination, respectively.
The following figure shows the sample map.
Note: It is guaranteed that all the stations are reachable, and all the queries consist of legal station numbers.
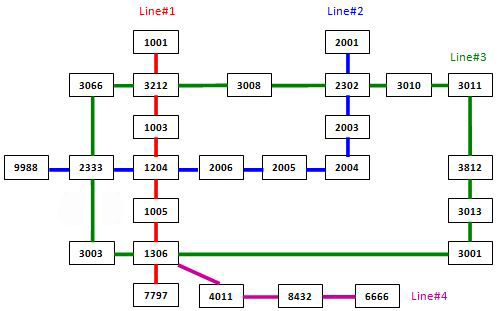
Output Specification:
For each query, first print in a line the minimum number of stops. Then you are supposed to show the optimal path in a friendly format as the following:
Take Line#X1 from S1 to S2.
Take Line#X2 from S2 to S3.
…
where Xi’s are the line numbers and Si’s are the station indices. Note: Besides the starting and ending stations, only the transfer stations shall be printed.
If the quickest path is not unique, output the one with the minimum number of transfers, which is guaranteed to be unique.
Sample Input:
4
7 1001 3212 1003 1204 1005 1306 7797
9 9988 2333 1204 2006 2005 2004 2003 2302 2001
13 3011 3812 3013 3001 1306 3003 2333 3066 3212 3008 2302 3010 3011
4 6666 8432 4011 1306
3
3011 3013
6666 2001
2004 3001
Sample Output:
2
Take Line#3 from 3011 to 3013.
10
Take Line#4 from 6666 to 1306.
Take Line#3 from 1306 to 2302.
Take Line#2 from 2302 to 2001.
6
Take Line#2 from 2004 to 1204.
Take Line#1 from 1204 to 1306.
Take Line#3 from 1306 to 3001.
Note
- 题意： 输出经过节点最少的规划，若最少相同，输出专程最少的规划
- 思路： 用数组记录两个车站之间的信息，这一点一开始并没有想到。Dfs遍历即可，
code1在dfs时记录node类型结果，dfs完直接输出，
code2记录最优规划经过节点的信息，dfs完成后再进行加工，显然，第二种方式要更方便 - line利用map存储， 将两个四位合成一个八位，（长见识le）, printf的时候忘记了04d 导致135测试点错误。
- 注意开始的时候 push和最后一点的输出
Code1
#include<bits/stdc++.h>
using namespace std;
const int maxn = 1e4;
const int inf = 1e9;
struct node{
int start;
int end;
int line;
};
vector<node> path, res;
vector<int> a[maxn];
int line[10000][10000];
int visited[maxn] = {0};
int num, queries, start, des, minstop = inf, mintraverse = inf;
void Dfs(int tempstart, int n, int stopcnt, int traversecnt, int templine){//依次 一条线的起点 当前节点 历经节点数 历经换乘节点数 当前线路
if(n == des){// 递归边界
node temp = {tempstart, n, templine};
path.push_back(temp); // 记录到终点的结果
if(stopcnt < minstop){
minstop = stopcnt;
mintraverse = traversecnt;
res = path;
}else if(stopcnt == minstop && traversecnt < mintraverse){
mintraverse = traversecnt;
res = path;
}
path.pop_back();// 弹出该结果
return ;
}
for(int i = 0; i < a[n].size(); i++){
if(visited[a[n][i]] == 0){
visited[a[n][i]] = 1;
if(line[n][a[n][i]] != templine && stopcnt != 0){ // 若换乘
node temp = {tempstart, n, templine};
path.push_back(temp);
Dfs(n, a[n][i], stopcnt + 1, traversecnt + 1, line[n][a[n][i]] );
path.pop_back();
visited[a[n][i]] = 0;
}
else {
int tempnext= a[n][i]; // 若不换乘
visited[a[n][i]] = 1;
Dfs(tempstart, tempnext, stopcnt + 1, traversecnt, line[n][a[n][i]]);
}
visited[a[n][i]] = 0;
}
}
}
int main(){
int i, j, tempnum, tempa;
cin >> num;
for(i = 0; i < num; i++){
cin >> tempnum;
int last = 0;
for(j = 0; j < tempnum; j++){
cin >> tempa;
if(j != 0){
line[tempa][last] = line[last][tempa] = i+1;
a[tempa].push_back(last);
a[last].push_back(tempa);
}
last = tempa;
}
}
cin >> queries;
while(queries--){
fill(visited, visited + maxn, 0);
cin >> start >> des;
path.clear();
res.clear();
minstop = inf; mintraverse = inf;
Dfs(start, start, 0, 0, line[start][a[start][0]]);
printf("%dn", minstop);
for(i = 0; i < res.size(); i++){
printf("Take Line#%d from %04d to %04d.n", res[i].line, res[i].start, res[i].end );
}
}
return 0;
}
Code2
#include<bits/stdc++.h>
using namespace std;
const int maxn = 1e5;
const int inf = 1e9;
vector<int> temppath, res;
vector<int> a[maxn];
map<int, int> line;
int visited[maxn] = {0};
int num, queries, start, des, minstop = inf, mintraverse = inf;
void Dfs(int n, int stopcnt, int traversecnt, int templine){
if((n == des) && ((stopcnt < minstop) || (stopcnt == minstop && traversecnt < mintraverse))){
mintraverse = traversecnt;
minstop = stopcnt;
res = temppath;
return ;
}
if(n == des) return;
for(int i = 0; i < a[n].size(); i++){
if(visited[a[n][i]] == 0){
temppath.push_back(a[n][i]);
visited[a[n][i]] = 1;
if(line[n * 10000 + a[n][i] ] != templine ) Dfs(a[n][i], stopcnt + 1, traversecnt + 1, line[n * 10000 + a[n][i]] );
else Dfs(a[n][i], stopcnt + 1, traversecnt, line[n * 10000 + a[n][i]]);
temppath.pop_back();
visited[a[n][i]] = 0;
}
}
}
int main(){
int i, j, tempnum, tempa;
cin >> num;
for(i = 0; i < num; i++){
cin >> tempnum;
int last = 0;
for(j = 0; j < tempnum; j++){
cin >> tempa;
if(j != 0){
line[tempa * 10000 + last] = line[last * 10000 + tempa] = i+1;
a[tempa].push_back(last);
a[last].push_back(tempa);
}
last = tempa;
}
}
cin >> queries;
while(queries--){
fill(visited, visited + maxn, 0);
cin >> start >> des;
temppath.clear();
minstop = inf; mintraverse = inf;
visited[start] =1; temppath.push_back(start);// 忘加第一点
Dfs(start, 0, 0, line[start * 10000 + a[start][0]]);
printf("%dn", minstop);
int last = 0, tempstart = start;
for(i = 0; i < res.size(); i++){
if(i != 0 && i < res.size() - 1){
if(line[last * 10000 + res[i] ] != line[res[i] * 10000 + res[i+1] ]){
printf("Take Line#%d from %04d to %04d.n", line[last * 10000 + res[i] ], tempstart, res[i]);
tempstart = res[i];
}
}else if(i == res.size() - 1) printf("Take Line#%d from %04d to %04d.n", line[last * 10000 + des ], tempstart, des);
last = res[i];
}
}
return 0;
}
最后
以上就是结实世界为你收集整理的1131 Subway Map (30 分) 思维Keywords: Dfs, 思维Input Specification:Output Specification:Sample Input:Sample Output:NoteCode1Code2的全部内容，希望文章能够帮你解决1131 Subway Map (30 分) 思维Keywords: Dfs, 思维Input Specification:Output Specification:Sample Input:Sample Output:NoteCode1Code2所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
发表评论 取消回复