从枚举到动态规划

动态规划特点

1、重叠子问题
2、状态转移方程（最关键）
3、最优子结构
题型：求最值
核心：穷举

解题套路

1、明确【状态】
2、明确【选择】
3、明确 dp函数/数组的定义
4、明确 base case

动态规划解法代码框架

//初始化 base case
dp[0][]0][...] = base
//进行状态转移
for 状态1 to 状态1的所有取值
    for 状态2 to 状态2的所有取值
        for ...
            dp[状态1][状态2][...] = 求最值（选择1，选择2...)
            

举个例子

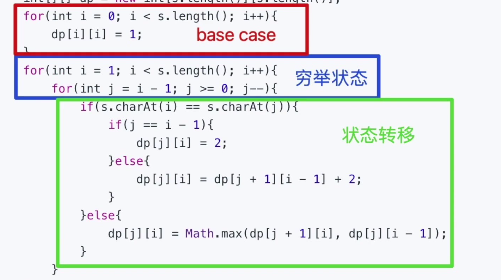
接下来上例题

斐波那数列

严格来说这不算动态规划，因为动态规划一般用来求最值，但是这道题可以清晰的展现出动态规划的过程。
斐波那数列用递归来解代码是这样的：

int fib(int n)
{
    if(n==1||n==2)
        return 1;
    return fib(n-1)+fib(n-2);
}

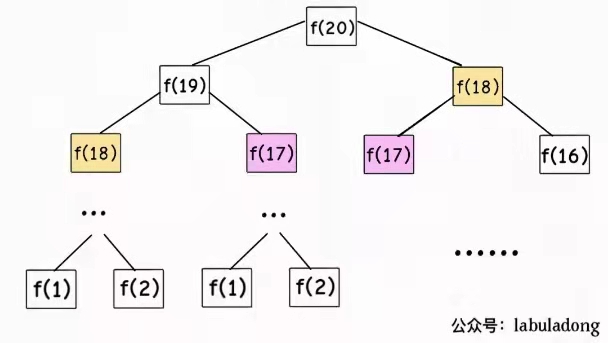
算法十分简洁，但是效率极低，在刷题时不出意外肯定会超时，像我们求 fib(20) 时要求出 fib(19) 和 fib(18) ,而求 fib(19) 时又要再求一次 fib(18) ,以此类推出现了很多相同的计算，做了很多无用功。

这就是问题所在，既然耗时的原因是重复计算，那么我们就可以造一个【备忘录】，每次算出某个子问题的答案记录到【备忘录】中，每次要计算子问题先查查【备忘录】，如果已经解决这个问题，直接拿答案来用。
下面将计算出来的结果存储在数组f[n]中。

int fib(int n)
{
    if(n==0||n==1)
        return f[n]=1;
    if(f[n])
        return f[n];
    return f[n]=fib(n-1)+fib(n-2);
}

至此，带备忘录的递归解法效率已经和迭代的动态规划一样了。实际上，这种解法和迭代的动态规划思想差不多，只不过这叫【自顶向下】，动态规划叫【自底向上】。

什么是【自顶向下】？
刚刚的递归树，是从上向下延伸，都是从大规模问题向下逐渐分解规模，直到触底（递归结束条件），然后逐层放回答案。

什么是【自底向上】？
反过来，我们直接从最底下，最简单，问题规模最小往上推，直到推出我们想要的答案，这就是动态规划的思路，也叫递推，这也是为什么动态规划一般都脱离了递归，而是由循环迭代完成计算。

void fib()
{
   f[0]=1;
   f[1]=1;
   for(int i=2;i<=n;i++)
     f[i]=f[i-1]+f[i-2];
}

什么叫【状态转移方程】
你把 f(n) 想做状态n，这个状态n由状态n-1和状态n-2相加转移而来，这就叫状态转移，仅此而已。但是上面几种解法中的所有操作都是围绕这个方程式的不同表现形式。可见列出【状态转移方程】的重要性，它是解决问题的核心。

凑零钱问题

先看下题目：给你k种面值的硬币，面值分别为c1, c2 … ck，每种硬币的数量无限，再给一个总金额amount，问你最少需要几枚硬币凑出这个金额，如果不可能凑出，算法返回 -1 。算法的函数签名如下：

// coins 中是可选硬币面值，amount 是目标金额
int coinChange(int* coins , int coinsSize , int amount);
比如说k = 3，面值分别为 1，2，5，总金额amount = 11。那么最少需要 3 枚硬币凑出，即 11 = 5 + 5 + 1。

你认为计算机应该如何解决这个问题？显然，就是把所有肯能的凑硬币方法都穷举出来，然后找找看最少需要多少枚硬币。

先确定「状态」
也就是原问题和子问题中变化的变量。由于硬币数量无限，所以唯一的状态就是目标金额amount。

然后确定dp函数的定义：
函数 dp(n)表示，当前的目标金额是n，至少需要dp(n)个硬币凑出该金额。

然后确定「选择」并择优
也就是对于每个状态，可以做出什么选择改变当前状态。具体到这个问题，无论当的目标金额是多少，选择就是从面额列表coins中选择一个硬币，然后目标金额就会减少。

最后明确 base case
显然目标金额为 0 时，所需硬币数量为 0；当目标金额小于 0 时，无解，返回 -1。

例如 amount = 11 , coins = {1, 2, 5} 时，画递归树。

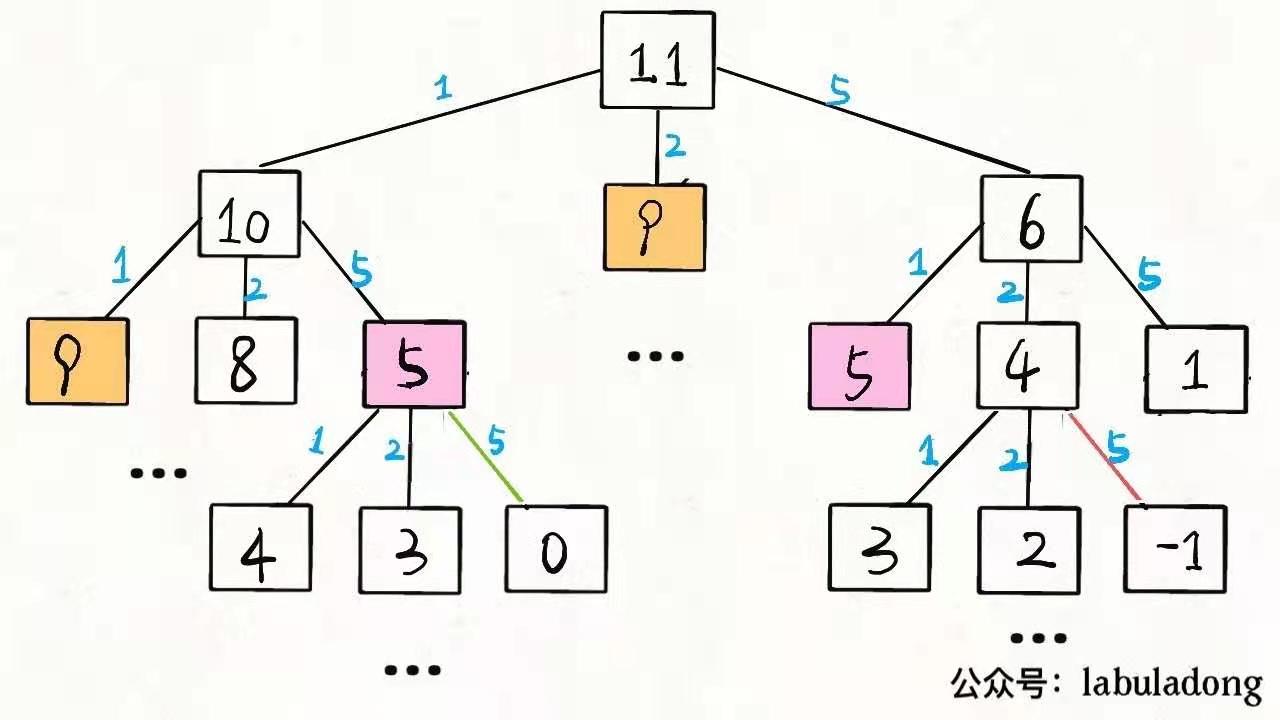
由图可以看出，要求出amount为11时要求出amount为10或amount为9或amount为6的最优解加一。

直接上动态规划代码

int coinChange(int *coins,int coinSize,int amount)
{
    if(amount==0)
        return 0;
    int dp[amount+1];
    dp[0]=0;
    for(int i=1;i<amount+1;i++)
      dp[i]=INT_MAX;     //初始化为最大值
    for(int i=1;i<=amount;i++)
    {
        for(int j=0;j<coinSize;j++)
            if(coins[j]<=i)                    //需要过滤-1的情况
                dp[i]=min(dp[i],(dp[i-coins[j]]+1));
    }
    return (dp[amount]>amount?-1:dp[amount];  
    //如果数组过大说明没法凑到这个钱数，放回-1;
}

动态规划问题总结

1、如何穷举
写出状态转移方程，暴力穷举所有可行解。

2、如何聪明地穷举
用备忘录消除重叠子问题，写出自顶向下的解法。
进一步，可以写出自底向上的迭代解法。
再进一步，可能可以优化空间复杂度。

最后，文章是观看微信公众号：labuladong 的视频后总结出，有兴趣的可去观看视频讲解学习。

最后

以上就是高挑期待为你收集整理的从枚举到动态规划的全部内容，希望文章能够帮你解决从枚举到动态规划所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。