西瓜书决策树实现（基于ID3）——采用字典数据结构

一、前言
这段时间疫情不那么严重，回公司上班了。平时工作比较忙，而且重点在学习数学。很久没有更新，最近实现《西瓜书》决策树，贴出来给大家共享。西瓜数据集2.0如下：在这里插入代码片
[‘青绿’, ‘蜷缩’, ‘浊响’, ‘清晰’, ‘凹陷’, ‘硬滑’, ‘好瓜’],
[‘乌黑’, ‘蜷缩’, ‘沉闷’, ‘清晰’, ‘凹陷’, ‘硬滑’, ‘好瓜’],
[‘乌黑’, ‘蜷缩’, ‘浊响’, ‘清晰’, ‘凹陷’, ‘硬滑’, ‘好瓜’],
[‘青绿’, ‘蜷缩’, ‘沉闷’, ‘清晰’, ‘凹陷’, ‘硬滑’, ‘好瓜’],
[‘浅白’, ‘蜷缩’, ‘浊响’, ‘清晰’, ‘凹陷’, ‘硬滑’, ‘好瓜’],
[‘青绿’, ‘稍蜷’, ‘浊响’, ‘清晰’, ‘稍凹’, ‘软粘’, ‘好瓜’],
[‘乌黑’, ‘稍蜷’, ‘浊响’, ‘稍糊’, ‘稍凹’, ‘软粘’, ‘好瓜’],
[‘乌黑’, ‘稍蜷’, ‘浊响’, ‘清晰’, ‘稍凹’, ‘硬滑’, ‘好瓜’],
[‘乌黑’, ‘稍蜷’, ‘沉闷’, ‘稍糊’, ‘稍凹’, ‘硬滑’, ‘坏瓜’],
[‘青绿’, ‘硬挺’, ‘清脆’, ‘清晰’, ‘平坦’, ‘软粘’, ‘坏瓜’],
[‘浅白’, ‘硬挺’, ‘清脆’, ‘模糊’, ‘平坦’, ‘硬滑’, ‘坏瓜’],
[‘浅白’, ‘蜷缩’, ‘浊响’, ‘模糊’, ‘平坦’, ‘软粘’, ‘坏瓜’],
[‘青绿’, ‘稍蜷’, ‘浊响’, ‘稍糊’, ‘凹陷’, ‘硬滑’, ‘坏瓜’],
[‘浅白’, ‘稍蜷’, ‘沉闷’, ‘稍糊’, ‘凹陷’, ‘硬滑’, ‘坏瓜’],
[‘乌黑’, ‘稍蜷’, ‘浊响’, ‘清晰’, ‘稍凹’, ‘软粘’, ‘坏瓜’],
[‘浅白’, ‘蜷缩’, ‘浊响’, ‘模糊’, ‘平坦’, ‘硬滑’, ‘坏瓜’],
[‘青绿’, ‘蜷缩’, ‘沉闷’, ‘稍糊’, ‘稍凹’, ‘硬滑’, ‘坏瓜’]
二、样本数据读取及存储
为了便于数据操作，每个数据样本存储为字典，字典key为样本各个特征，比如纹理，敲声等，字典value对应特征标签值，比如清晰、沉闷。

def read_data(filename):
    
    """
    Function : 读取西瓜数据集
    
    Input: filename: 数据集文件名
          
    Output: data:西瓜数据集列表，列表元素为字典，每个字典保存西瓜属性
           
    """
    
    text_list = []
    with open(filename,"r") as f:
        #当读到最后一行的下一行时，line 为空集，停止读取
        while True:
            line = f.readline()
            if not line:
                break
            #删除每行尾换行符
            line = line.strip("n")
            #s删除每行头尾空格
            line = line.strip(" ")
            #删除每行头尾的[ ，]
            line = line.strip("[")
            line = line.strip(",")
            line = line.strip("]")
            if line != "":
                text_list.append(line)
    
    #创建数据列表，每个西瓜数据为一个字典，字典形成列表
    dataset = []
    
   
    for i,text_line in enumerate(text_list):
        
        #把每行字符串分割为列表
        split_data_text = text_line.split( ",")
        
        #每个西瓜数据初始化一个字典对象并保存该西瓜的数据
        dic_example = {}
        dic_example["编号"] = i + 1
        #删除每个特征标签的引号和空格
        dic_example["色泽"] = split_data_text[0].replace("'","").strip()
        dic_example["根蒂"] = split_data_text[1].replace("'","").strip()
        dic_example["敲声"] = split_data_text[2].replace("'","").strip()
        dic_example["纹理"] = split_data_text[3].replace("'","").strip()
        dic_example["脐眼"] = split_data_text[4].replace("'","").strip()
        dic_example["触感"] = split_data_text[5].replace("'","").strip()
        dic_example["标签"] = split_data_text[6].replace("'","").strip()
        
        #将西瓜数据字典加入列表
        dataset.append(dic_example)
                
    return dataset
    #建立数据集

数据读取结果如下：

filename = "西瓜数据集2.0.txt"
dataset = read_data(filename)

[{'编号': 1,
  '色泽': '青绿',
  '根蒂': '蜷缩',
  '敲声': '浊响',
  '纹理': '清晰',
  '脐眼': '凹陷',
  '触感': '硬滑',
  '标签': '好瓜'},
 {'编号': 2,
  '色泽': '乌黑',
  '根蒂': '蜷缩',
  '敲声': '沉闷',
  '纹理': '清晰',
  '脐眼': '凹陷',
  '触感': '硬滑',
  '标签': '好瓜'},
 {'编号': 3,
  '色泽': '乌黑',
  '根蒂': '蜷缩',.............
  共17个字典数据构成列表

三、决策树生成思路
整体思路是按照西瓜书的伪代码流程来的，关键步骤是生成判别树时候要使用递归函数。我之前思路是像二叉树那样自己定义结点数据结构和树的数据结构，后来参考了别人做法，为了使用统一的画图函数，直接采用字典嵌套来表示决策树。其实字典本来就可能完美定义各种树，因为字典的键以随意添加，每个键就是结点的分支。分支的值有2种情况，一种情况是分支为子结点情况，此时分支的值（即字典key对应的value）为判别结果“好瓜”、“坏瓜”。一种是该分支又继续有分支，那么该分支的值(即字典key对应的值)应该还是一个字典。
递归函数是解决树问题的有效工具，递归函数的基本要素有两个：一是递归函数终止或者返回条件，二是递归函数的传递条件。
本问题中递归函数终止条件伪代码中已经明示，共有4种情况：
1.该分支样本数为0，那么该分支的值取为其父节点样本中出现次数最多的判别标签。
2…该分支有样本，但是分支所有样本的判别标签相同，即要么全部为好瓜，要么全部为坏瓜，这种情况自然不需再有分支，直接将其取值定为样本的判别标签即可。
3.该分支有样本，但是随着判断的进行，不断选择和丢弃最优特征，最后可以用来判别的特征（指的是纹理、敲声等）用完了，这时候无法选择最优特征，也就无法生成分支，于是只能把该分支的值定为分支中样本出现最多次的标签。
4.该分支有样本，但是如果分支的样本所有特征的标签都是相同的（判别标签不同），那么可以直接选择出现最多的判别标签作为该分支的值即可。因为如果所有样本的特征标签相同，那么所有特征的信息增益都相同，这种情况下是没有最优特征的，直接选择出现最多的样本判别标签作为分支值即可。

于是生成决策树的主函数如下：

def TreeGenerate(node_dataset, A):
    
    """
    Function : 根据样本列表和特征列表生成判别字典
    
    Input: node_dataset: 当前结点的数据集，列表，元素为字典类型
           A: 可以选择的特征列表
    
    Output: 判别字典
           
    """
    #对应终止条件2，判断节点内样本的判别标签是否相同，如果相同则返回样本判别标签
    if  is_the_same_jugement(node_dataset):
        return node_dataset[0]["标签"]
 #对应终止条件3,4如果样本判别的剩余属性数量为0，或者样本特征标签全部相同，将样本标签定义为数量最多的样本对应的标签，并且将其返回
    if len(A) == 0 or is_the_same_labels(node_dataset, A):
        return argmax_jugement(node_dataset)
    
    
    #判别各个特征ai，找出信息增益最大的ai_best
    ai_best = select_ai(node_dataset, A)
    
    
    
    #以ai_best为属性，生成字典
    my_tree = {ai_best: {}}
    
    #根据最优特征ai_best的标签值，将节点样本重新分组
    
    sub_node_datasets= classfide_by_ai_best(node_dataset,ai_best )
    
    #移除A中本次使用的最优特征
    A.remove(ai_best)
        #遍历ai_best 特征的标签值
    for ai_best_value in  sub_node_datasets.keys():
        #注意此时必须使用切片复制的方法，若直接采用sub_A = A，则sub_A中删除最优特征时，A中元素也会删除对应最优特征，
        #，导致同一个根节点的不同分支，随着递归进行，可选的剩余特征越来越少
        sub_A = A[:]
        
        #获取最大增益特征的标签值对应的样本列表
        sub_node_dataset =  sub_node_datasets[ai_best_value]
        #对应返回情况1，如果最大增益特征的某一个标签值对应的样本列表为空，将分支结点定为叶结点，判别标签标记为父节点的样本最多的类标签
        if len(sub_node_dataset) == 0:
            my_tree[ai_best][ai_best_value] = argmax_jugement(node_dataset)
            #空集分支判断结束，进入最优特征的下一个标签结点
            continue
            
        #递归调用本函数，函数自变量为子样本列表和剩余特征列表，函数返回判别标签
        subTree = TreeGenerate(sub_node_dataset, sub_A)
        #把新生成的子树赋值给根节点的分支，分支的结点值为ai_best的标签值
        my_tree[ai_best][ai_best_value] = subTree
    return my_tree
       

四、功能函数实现
主函数完成后，就是功能函数实现了，这里不再多说，看注释即可

def Cal_info_entrop(node_dataset):
    """
    Function : 计算某结点的信息熵
    
    Input: node_dataset: 当前结点的数据集，列表对象
    
    Output: entrop:当前结点的信息熵
           
    """
#计算结点内样本数量
    number_of_example = len(node_dataset)
    
    #创建标签统计字典
    label_stastics = {}
    
    for data in node_dataset:
        #如果标签不在标签字典里，在字典里创建标签作为key并赋值为0
        if data["标签"] not in label_stastics.keys():
            label_stastics[data["标签"]] = 0
        #对应分类标签加1
        label_stastics[data["标签"]] += 1
        
    entrop = 0.0
    
    #根据标签分类字典计算信息熵
    for key in label_stastics.keys():
        pk = float(label_stastics[key] / number_of_example)
        entrop +=  - pk * np.log2(pk)
    
    return entrop
 

def Cal_info_gain(node_dataset, feature):
    """
    Function : 计算结点内某一个属性的信息增益    
    Input: node_dataset: 当前结点的数据集，列表对象
           feature:计算信息增益所采用的属性        
    Output: entrop:信息增益
           
    """
    #计算结点内样本数量
    D = len(node_dataset)
    
    #根据样本的feature类别数将样本分为不同的列表，列表元素为样本字典对象，每一个列表里的样本属性拥有相同的特征值
    feature_stastic = {}
    #import pdb
    #pdb.set_trace()
    for data in node_dataset:
        
        #判断字典中是否有属性的特征值，如果没有，则在字典中新建该键值项，其值为空列表
        if data[feature] not in feature_stastic.keys():
            feature_stastic[data[feature]] = []
            
         #把样本按照属性特征值放入不同的列表   
        feature_stastic[data[feature]].append(data)
    
    #计算结点所有样本的信息熵 （公式4.1）   
    EntD = Cal_info_entrop(node_dataset)
    Info_gain = EntD 
    #计算属性分类子集的信息熵
   
    for key in feature_stastic.keys():        
        #获取字典列表的样本数
        Dv = len(feature_stastic[key])
        #计算字典列表的信息熵（即计算对该属性分类后的子集合的信息熵）
        EntDv = Cal_info_entrop(feature_stastic[key])
        #计算信息增益（公式4.2）
        Info_gain = Info_gain - Dv / D * EntDv
   
    return  Info_gain

def is_the_same_jugement(node_dataset):
    """
    Function : 判断结点data是否为同个标签的样本
    Input: node_dataset: 当前结点的数据集，列表对象
    Output: True:是同一个标签，
           False: 不是同一个标签      
    """
    datalabel =  node_dataset[0]["标签"]
    for data in node_dataset:
        if datalabel !=  data["标签"]:
            return False
    return True

def argmax_jugement(node_dataset):
    
    """
    Function : 找出结点data样本中，包含最多样本的标签
    
    Input: node_dataset: 当前结点的数据集，列表对象
    
    Output: 标签
           
    """
    #统计不同标签对应的样本个数，存放到字典
    label_stastics = {}
    for data in node_dataset:
        #如果标签不在标签字典里，在字典里创建标签作为key并赋值为0
        if data["标签"] not in label_stastics.keys():
            label_stastics[data["标签"]] = 0
        #对应分类标签加1
        label_stastics[data["标签"]] += 1
    
    #找到样本数量最大的标签值
    max_label = max(label_stastics, key = label_stastics.get)
    
    return max_label

def is_the_same_labels(node_dataset,A):
    """
    Function : 判别结点data样本中，剩余特征的标签是否相同
    
    Input: node_dataset: 当前结点的数据集，列表对象
           A: 可以选择的特征列表
    
    Output: 若特征标签完全相同，返回Ture，否则返回False
           
    """
    #遍历剩余特征
    for av in A:
    #遍历所有样本的特征标签
        for data in node_dataset:  
            #如果第一个样本的标签值与其他任何样本不同，返回False
            if node_dataset[0][av] != data[av]:
                return False
    return True
 

def select_ai(node_dataset, A):
    
    """
    Function : 找出样本中信息增益最大的特征
    
    Input: node_dataset: 当前结点的数据集，列表对象
            A: 可以选择的特征列表
    
    Output: 信息增益最大的特征
           
    """
    Max_info_gain = 0.00
    ai_best = "找不到"
    for ai in A:
        Info_gain = Cal_info_gain(node_dataset, ai)
        if Info_gain > Max_info_gain:
            Max_info_gain = Info_gain
            ai_best = ai
            
    return ai_best

def get_the_feature_label_dic(dataset):
    
    """
    Function : 根据原始样本集，生产每个特征和对应的标签数据映射
    
    Input: node_dataset: 原始数据集，列表，元素为字典类型
           
    
    Output: 样本的特征取值，字典key为样本特征，value为列表，列表元素为样本特征的标签
           
    """
    feature_label_dic = {}
    for data in dataset:
        for key in data.keys():
            if key  not in feature_label_dic.keys():
                feature_label_dic[key] = []
            if data[key]  not in feature_label_dic[key]:
                feature_label_dic[key].append(data[key])
    return feature_label_dic

def classfide_by_ai_best(node_dataset,ai_best):
    
    """
    Function : 根据样本列表和最大增益特征，将列表中的样本按特征标签分类
    
    Input: node_dataset: 当前结点的数据集，列表，元素为字典类型
           ai_best:作为分类依据的特征
    
    Output: 样本的分类字典，字典key为aiv,value为对应的列表，列表元素为特征标签相同的样本，比如特征纹理同为标签模糊的样本集合
           
    """
        #统计不同标签对应的样本个数，存放到字典
    sub_node_datasets = {}
    #为最优特征的每个标签生成key_value键值对
    for ai_value in feature_label_dic[ai_best]:
        sub_node_datasets[ai_value] = []
        
    for data in node_dataset:
    #对应分类标签的value为列表，将data加入列表内，若该标签没有对应样本，则列表长度为0
        sub_node_datasets[data[ai_best]].append(data)
    return  sub_node_datasets

五、绘图程序
绘图程序参考《机器学习实战》

# @Time    : 2017/12/18 19:46
# @Author  : Leafage
# @File    : treePlotter.py
# @Software: PyCharm

import matplotlib.pylab as plt
import matplotlib

# 能够显示中文
matplotlib.rcParams['font.sans-serif'] = ['SimHei']
matplotlib.rcParams['font.serif'] = ['SimHei']

# 分叉节点，也就是决策节点
decisionNode = dict(boxstyle="sawtooth", fc="0.8")

# 叶子节点
leafNode = dict(boxstyle="round4", fc="0.8")

# 箭头样式
arrow_args = dict(arrowstyle="<-")


def plotNode(nodeTxt, centerPt, parentPt, nodeType):
    """
    绘制一个节点
    :param nodeTxt: 描述该节点的文本信息
    :param centerPt: 文本的坐标
    :param parentPt: 点的坐标，这里也是指父节点的坐标
    :param nodeType: 节点类型,分为叶子节点和决策节点
    :return:
    """
    createPlot.ax1.annotate(nodeTxt, xy=parentPt, xycoords='axes fraction',
                            xytext=centerPt, textcoords='axes fraction',
                            va="center", ha="center", bbox=nodeType, arrowprops=arrow_args)


def getNumLeafs(myTree):
    """
    获取叶节点的数目
    :param myTree:
    :return:
    """
    # 统计叶子节点的总数
    numLeafs = 0

    # 得到当前第一个key，也就是根节点
    firstStr = list(myTree.keys())[0]

    # 得到第一个key对应的内容
    secondDict = myTree[firstStr]

    # 递归遍历叶子节点
    for key in secondDict.keys():
        # 如果key对应的是一个字典，就递归调用
        if type(secondDict[key]).__name__ == 'dict':
            numLeafs += getNumLeafs(secondDict[key])
        # 不是的话，说明此时是一个叶子节点
        else:
            numLeafs += 1
    return numLeafs


def getTreeDepth(myTree):
    """
    得到数的深度层数
    :param myTree:
    :return:
    """
    # 用来保存最大层数
    maxDepth = 0

    # 得到根节点
    firstStr = list(myTree.keys())[0]

    # 得到key对应的内容
    secondDic = myTree[firstStr]

    # 遍历所有子节点
    for key in secondDic.keys():
        # 如果该节点是字典，就递归调用
        if type(secondDic[key]).__name__ == 'dict':
            # 子节点的深度加1
            thisDepth = 1 + getTreeDepth(secondDic[key])

        # 说明此时是叶子节点
        else:
            thisDepth = 1

        # 替换最大层数
        if thisDepth > maxDepth:
            maxDepth = thisDepth

    return maxDepth


def plotMidText(cntrPt, parentPt, txtString):
    """
    计算出父节点和子节点的中间位置，填充信息
    :param cntrPt: 子节点坐标
    :param parentPt: 父节点坐标
    :param txtString: 填充的文本信息
    :return:
    """
    # 计算x轴的中间位置
    xMid = (parentPt[0]-cntrPt[0])/2.0 + cntrPt[0]
    # 计算y轴的中间位置
    yMid = (parentPt[1]-cntrPt[1])/2.0 + cntrPt[1]
    # 进行绘制
    createPlot.ax1.text(xMid, yMid, txtString)


def plotTree(myTree, parentPt, nodeTxt):
    """
    绘制出树的所有节点，递归绘制
    :param myTree: 树
    :param parentPt: 父节点的坐标
    :param nodeTxt: 节点的文本信息
    :return:
    """
    # 计算叶子节点数
    numLeafs = getNumLeafs(myTree=myTree)

    # 计算树的深度
    depth = getTreeDepth(myTree=myTree)

    # 得到根节点的信息内容
    firstStr = list(myTree.keys())[0]

    # 计算出当前根节点在所有子节点的中间坐标,也就是当前x轴的偏移量加上计算出来的根节点的中心位置作为x轴（比如说第一次：初始的x偏移量为：-1/2W,计算出来的根节点中心位置为：(1+W)/2W，相加得到：1/2），当前y轴偏移量作为y轴
    cntrPt = (plotTree.xOff + (1.0 + float(numLeafs))/2.0/plotTree.totalW, plotTree.yOff)

    # 绘制该节点与父节点的联系
    plotMidText(cntrPt, parentPt, nodeTxt)

    # 绘制该节点
    plotNode(firstStr, cntrPt, parentPt, decisionNode)

    # 得到当前根节点对应的子树
    secondDict = myTree[firstStr]

    # 计算出新的y轴偏移量，向下移动1/D，也就是下一层的绘制y轴
    plotTree.yOff = plotTree.yOff - 1.0/plotTree.totalD

    # 循环遍历所有的key
    for key in secondDict.keys():
        # 如果当前的key是字典的话，代表还有子树，则递归遍历
        if isinstance(secondDict[key], dict):
            plotTree(secondDict[key], cntrPt, str(key))
        else:
            # 计算新的x轴偏移量，也就是下个叶子绘制的x轴坐标向右移动了1/W
            plotTree.xOff = plotTree.xOff + 1.0/plotTree.totalW
            # 打开注释可以观察叶子节点的坐标变化
            # print((plotTree.xOff, plotTree.yOff), secondDict[key])
            # 绘制叶子节点
            plotNode(secondDict[key], (plotTree.xOff, plotTree.yOff), cntrPt, leafNode)
            # 绘制叶子节点和父节点的中间连线内容
            plotMidText((plotTree.xOff, plotTree.yOff), cntrPt, str(key))

    # 返回递归之前，需要将y轴的偏移量增加，向上移动1/D，也就是返回去绘制上一层的y轴
    plotTree.yOff = plotTree.yOff + 1.0/plotTree.totalD


def createPlot(inTree):
    """
    需要绘制的决策树
    :param inTree: 决策树字典
    :return:
    """
    # 创建一个图像
    fig = plt.figure(1, facecolor='white')
    fig.clf()
    axprops = dict(xticks=[], yticks=[])
    createPlot.ax1 = plt.subplot(111, frameon=False, **axprops)
    # 计算出决策树的总宽度
    plotTree.totalW = float(getNumLeafs(inTree))
    # 计算出决策树的总深度
    plotTree.totalD = float(getTreeDepth(inTree))
    # 初始的x轴偏移量，也就是-1/2W，每次向右移动1/W，也就是第一个叶子节点绘制的x坐标为：1/2W，第二个：3/2W，第三个：5/2W，最后一个：(W-1)/2W
    plotTree.xOff = -0.5/plotTree.totalW
    # 初始的y轴偏移量，每次向下或者向上移动1/D
    plotTree.yOff = 1.0
    # 调用函数进行绘制节点图像
    plotTree(inTree, (0.5, 1.0), '')
    # 绘制
    plt.show()

六、运行结果
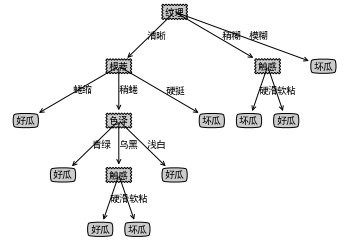
代码运行后生成的判别树如下：

my_tree = TreeGenerate(dataset, A)

{'纹理': {'清晰': {'根蒂': {'蜷缩': '好瓜',
    '稍蜷': {'色泽': {'青绿': '好瓜',
      '乌黑': {'触感': {'硬滑': '好瓜', '软粘': '坏瓜'}},
      '浅白': '好瓜'}},
    '硬挺': '坏瓜'}},
  '稍糊': {'触感': {'硬滑': '坏瓜', '软粘': '好瓜'}},
  '模糊': '坏瓜'}}

绘图：

createPlot(my_tree)

最后

以上就是年轻缘分为你收集整理的西瓜书决策树实现（基于ID3）——采用字典数据结构的全部内容，希望文章能够帮你解决西瓜书决策树实现（基于ID3）——采用字典数据结构所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。