动态数组怎么定义_动态规划｜分割等和子集

180 阅读 0 评论 119 点赞

我是靠谱客的博主苗条巨人，最近开发中收集的这篇文章主要介绍动态数组怎么定义_动态规划｜分割等和子集，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

动态规划｜分割等和子集

今天一起来学习Leetcode第 416 题：分割等和子集。

题目描述

题目分析

这是一道中等难度的题目。可能很多同学初看这道题目没有什么想法，但如果我们可以转变一下思路，这道题是不是说「我们是否可以从给定的数组中挑出一些数，这些数的总和恰好是数组总和的一半」。

有没有感觉很熟悉，我们想一下背包问题的问题描述：「我们是否可以从给定的物品中挑出一些物品，使得这些物品恰好可以装满整个背包」。

其实这道题本质上就是一道「背包问题」。

既然我们可以将这道题转化为常见的背包问题，那么这道题的解题思路也就大概明确了，我们应该使用「动态规划」的思想来解决这道题。

我们首先定义一个二维的动态规划数组dp[n][m+1]，并将其全部初始化为False。其中n 表示物品的总个数，而 m 表示数组总和的一半。dp 数组在容量这里多加一维是为了考虑容量为0 这个边界条件。

定义好了dp数组之后，我们看一下dp[i][j] 的含义，我们定义状态dp[i][j] 为在前i个物品中存不存在一种选择的可能性，使得它们的总和为j。如果存在，我们就将dp[i][j]的值置为True。

定义好了状态dp[i][j]，我们怎么进行状态的转移呢？也就是说我们怎么不断填满我们的dp数组呢?

其实这里的状态转移和我们人做选择时候很像，对于元素i, 只有两种选择的可能性，「放或者是不放」。

如果我们如果选择不放第 i 个物品，那么dp[i][j]=dp[i-1][j]。

如果我们选择放第 i 个物品，那么 dp[i][j]=dp[i-1][j-nums[i]]，当然这里的前提条件是 j>=nums[i]。

可能有些同学有些蒙，我们来手动画一下状态转移图来加深一下理解:

上面这个就是我一步一步推导的状态转移过程，有了上面的分析之后，我们可以写出代码

题目代码

class Solution:
    def canPartition(self, nums: List[int]) -> bool:
        total_sum = sum(nums)
        n = len(nums)
        if total_sum%2==1:
            return False
        
        half_sum = total_sum//2
        dp = [[0]*(half_sum+1) for i in range(n)]
        if nums[0]<=half_sum:
            dp[0][nums[0]]=1
        
        for i in range(n):
            dp[i][0]=1

        for i in range(1,n):
            for j in range(half_sum+1):
                dp[i][j] = dp[i-1][j]
                if nums[i]<=j:
                    dp[i][j] = dp[i-1][j] or dp[i-1][j-nums[i]]
        return dp[-1][-1]

当然，我们由上面的推导过程可以发现，只要我们当发现dp[i][-1]=1的时候，就说明前i个元素就可以等于我们的既定目标，那么我们就可以直接结束我们的程序，从而完成剪枝。所以我们对代码进行一些优化：

class Solution:
    def canPartition(self, nums: List[int]) -> bool:
        total_sum = sum(nums)
        n = len(nums)
        if total_sum%2==1:
            return False
        
        half_sum = total_sum//2
        dp = [[0]*(half_sum+1) for i in range(n)]
        if nums[0]<=half_sum:
            dp[0][nums[0]]=1
        
        for i in range(n):
            dp[i][0]=1

        for i in range(1,n):
            for j in range(half_sum+1):
                dp[i][j] = dp[i-1][j]
                if nums[i]<=j:
                    dp[i][j] = dp[i-1][j] or dp[i-1][j-nums[i]]
            if dp[i][-1]==1:
              return True
        return dp[-1][-1]

代码优化

当然，和背包问题一样，我们可以对算法的空间复杂度进一步优化。上述代码的空间复杂度为O(mn)，我们可以将其降到O(m)。

降低空间复杂度的核心motivation在于，我们发现，dp[i][:]的更新仅仅依赖于dp[i-1][:]，和dp[i-2][:] 或者更往前的状态是无关的；并且dp[i][j]的状态仅仅和dp[i-1][j] 以及 dp[i-1][j-nums[i]] 相关，如下图所示：

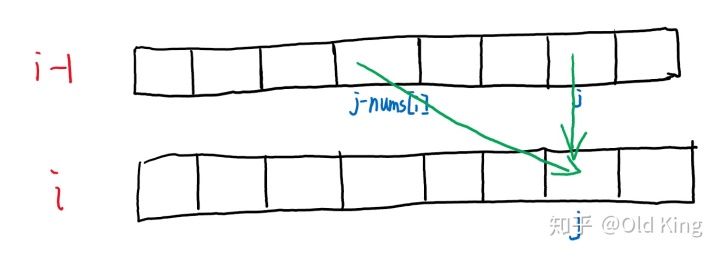
因此，之前的历史状态其实是可以不保存的；我们可以仅仅维护一个动态数组dp[m+1]，而其中最核心的技巧就是将j从大到小更新，这样上一轮dp[j-nums[i]]的值就可以在这一轮更新dp[j]的时候保持不变，代码如下：

class Solution:
    def canPartition(self, nums: List[int]) -> bool:
        total_sum = sum(nums)
        n = len(nums)
        if total_sum%2==1:
            return False 
        half_sum = total_sum//2
        dp = [0]*(half_sum+1)
        dp[0]=1
        if nums[0]<=half_sum:
            dp[nums[0]]=1
        for i in range(1,n):
            for j in range(half_sum,-1,-1):
                if nums[i]<=j:
                    dp[j] = dp[j] or dp[j-nums[i]]
        return dp[-1]