[1]进制转化,原反补码以及综合例题
1>进制加减法
进行加法运算时逢 几 进1,进行减法运算时借1当 几
2>二进制、八进制、十六进制转换为十进制

3>十进制转换为二进制、八进制、十六进制
整数部分:除 几 取余
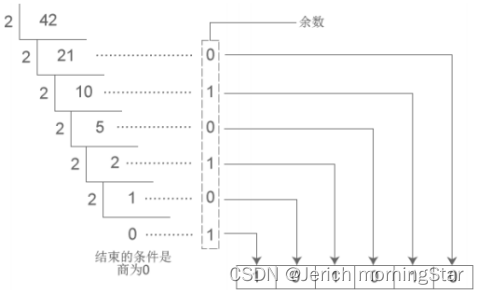
小数部分:乘 几 取整
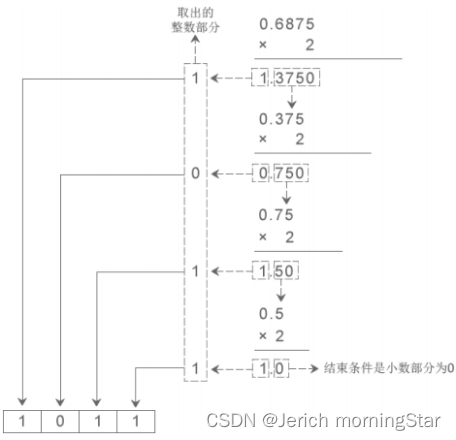
4>二进制和八进制,以及二进制和十六进制之间的转换
-
二—>八:三合一,不够0补
-
八—>二:一分三
-
二—>十六:四合一,不够0补
-
十六—>二:一分四
5>原码、反码、补码
符号位表示:0表示正 、1表示负
-
正数:原反补码都相同
-
负数:反码 = 原码符号位不变,其它位取反
补码 = 反码 + 1
6>综合例题
0x12345678,将该数的第8-10位设置为Ox7,12-14位设置为0x6,其他位保持不变
0001 0010 0011 0100 0101 0110 0111 1000 //原码
0000 0000 0000 0000 0000 0111 0000 0000 //0x7<<8
0001 0010 0011 0100 0101 0111 0111 1000 //GPX2CON = GPX2CON | (0x7<<8)
0000 0000 0000 0000 0111 0000 0000 0000 //0x7<<12
1111 1111 1111 1111 1000 1111 1111 1111 //取反:~( 0x7<<12)
0001 0010 0011 0100 0000 0111 0111 1000 //清零:GPX2CON = GPX2CON & ~(0x7<<12)
0000 0000 0000 0000 0110 0000 0000 0000 //0x6<<12
0001 0010 0011 0100 0110 0111 0111 1000 //置位
GPX2CON = GPX2CON & ~(0x7<<12) | 0x6<<12 = 0x12346778
[2] gcc编译流程
GCC把源文件生成操作系统可以执行的文件需要经历4个过程
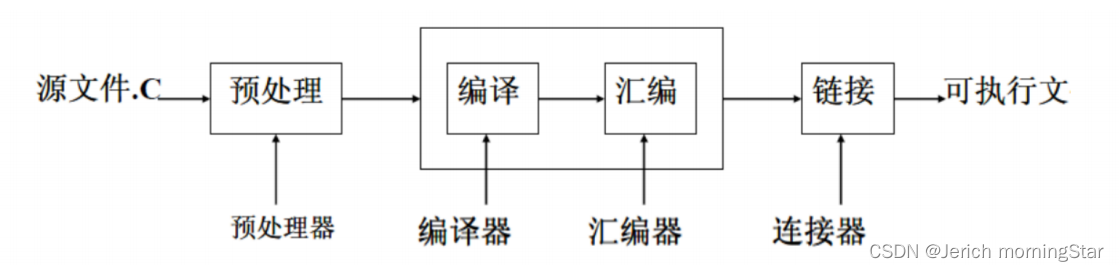
| 后缀名 | 对应的语言 |
|---|---|
| -c | 只编译不链接,生成目标文件".o" |
| -S | 只编译不汇编,生成汇编代码 |
| -E | 只进行预编译,不做其他处理 |
| -g | 在可执行程序种包含标准调试信息 |
| -o file | 把输出文件输出到file里 |
| -v | 打印出编译器内部编译各过程的命令行信息和编译器的版本 |
1> 预处理阶段
去掉注释,加载头文件,代替宏定义,条件编译
条件编译 需要文件:.c文件 生成产物:预处理文件(以.i结尾)
gcc -E [源文件] -o [目标文件]
实例:gcc -E hello.c -o hello.i
后缀名为”.i”的文件是经过预处理后的C原始程序。
2> 编译
编译阶段的主要工作是把我们的源代码生成相应的汇编代码的过程。这个阶段花费的时间会比较长。它需要对我们的C语言进行语法和语义的分析。如果有语法错误,报错,并结束编译过程。如果没有语法错误,还需要优化我们的代码,把C的源程序转变为汇编代码。需要文件:.i文件 生成产物:汇编文件(以.s结尾)。
gcc -S [源文件] -o [目标文件]
实例:gcc -S hello.i -o hello.s
后缀名为”.s”的文件是汇编语言原始程序。
3> 汇编
首先我们应该知道汇编代码(汇编指令)并不是机器能够执行的语言。我们还必须把汇编语言翻译
成计算机能识别的机器语言,这个翻译的过程是在汇编阶段完成的。所以在这个阶段把汇编源文件通过
汇编器生成目标文件(二进制机器语言)。
gcc -c [源文件] -o [目标文件]
实例:gcc -c hello.s -o hello.o
C 语言代码经过编译以后,并没有生成最终的可执行文件(.exe 文件),而是生成了一种叫做目标文件(Object File)的中间文件(或者说临时文件)。目标文件也是二进制形式的,它和可执行文件的格式是一样的。对于 Visual C++,目标文件的后缀是.obj;对于 GCC,目标文件的后缀是.o。
4> 链接
把目标文件执行所依赖的所有二进制的其他目标文件及C的库文件都整合成一个可执行文件的过程需要文件:.o文件及各种动态库或静态库
生成产物:可执行程序。
gcc [源文件] -o [目标文件]
实例:gcc hello.o -o hello
汇编只是将我们自己写的代码变成了二进制形式,它还需要和系统组件(比如标准库、动态链接库
等)结合起来, 链接(Link)其实就是一个“打包”的过程,它将所有二进制形式的目标文件和系统组件组合成
一个可执行文件。
[3]运算符优先级
| 优先级 | 运算符 | 名称或含义 | 使用形式 | 结合方向 | 说明 |
|---|---|---|---|---|---|
| 1 | [ ] | 数组下标 | 数组名[ ] | 左到右 | |
| ( ) | 圆括号 | (表达式) /函数名(形参表) | |||
| . | 成员选择(对象) | 对象.成员名 | |||
| -> | 成员选择(指针) | 对象指针->成员名 | |||
| 2 | - | 负号运算符 | -表达式 | 右到左 | 单目运算符 |
| ~ | 按位取反 | ~表达式 | |||
| ++ | 自增 | ++变量名、变量名++ | |||
| – | 自减 | –变量名、变量名– | |||
| * | 取值运算符 | *指针变量 | |||
| & | 取地址 | &变量名 | |||
| ! | 逻辑非 | !(表达式) | |||
| (类型) | 强制转换 | (数据类型)表达式 | |||
| sizeof | 长度运算符(字节) | sizeof(表达式) | |||
| 3 | / | 除 | 表达式/表达式 | 左到右 | 双目运算符 |
| * | 乘 | 表达式*表达式 | |||
| % | 取余 | 表达式%表达式 | |||
| 4 | + | 加 | 表达式+表达式 | ||
| - | 减 | 表达式-表达式 | |||
| 5 | << | 左移 | 变量<<(表达式) | ||
| >> | 右移 | 变量>>(表达式) | |||
| 6 | > | 大于 | 表达式>表达式 | 左到右 | 双目运算符 |
| >= | 大于等于 | 表达式>=表达式 | |||
| < | 小于 | 表达式<表达式 | |||
| <= | 小于等于 | 表达式<=表达式 | |||
| 7 | == | 等于 | 表达式==表达式 | ||
| != | 不等于 | 表达式!=表达式 | |||
| 8 | & | 按位与 | 表达式&表达式 | 左到右 | 双目运算符 |
| 9 | ^ | 按位异或 | 表达式^表达式 | ||
| 10 | | | 按位或 | 表达式|表达式 | ||
| 11 | && | 逻辑与 | 表达式&&表达式 | ||
| 12 | || | 逻辑或 | 表达式||表达式 | ||
| 13 | ? : | 条件运算符 | 表达式1 ? 表达式2 : 表达式3 | 右到左 | 三目运算符 |
| 14 | = | 赋值 | 变量=表达式 | 右到左 | |
| /= | 除后赋值 | 变量/=表达式 | |||
| *= | 乘后赋值 | 变量*=表达式 | |||
| %= | 取余后赋值 | 变量%=表达式 | |||
| += | 加后赋值 | 变量+=表达式 | |||
| -= | 减后赋值 | 变量-=表达式 | |||
| <<= | 左移后赋值 | 变量<<=表达式 | |||
| >>= | 右移后赋值 | 变量>>=表达式 | |||
| &= | 按位与后赋值 | 变量&=表达式 | |||
| ^= | 按位异或后赋值 | 变量^=表达式 | |||
| |= | 按位或后赋值 | 变量|=表达式 | |||
| 15 | , | 逗号 | 表达式1,表达式2,表达式3… | 左到右 |
[4]linux下使用sqrt函数问题
程序引用头文件math.h;
gcc编译时需要在.c后面加上**-lm**
如:gcc test.c -lm -o test
[5]linux终端左右分屏
-
1>安装tmux工具:sudo apt-get install tmux
-
2>使用工具:tmux
-
3>左右分屏:ctrl + b 再按 %
-
4>切换屏幕:ctrl + b 再按 o
-
5>关闭一个终端:ctrl + b 再按x
[6]while循环中printf打印两次问题
原因:按下回车键’n’被视为字符,同样进入while循环里的语句判断,造成printf重复执行了两次
解决办法:在获取键盘输入后,加入以下代码,消耗内存中的’n’
while(getchar()!='n')
continue;
[7]输出斐波那契数列前n项以及前n项和(函数+递归)
首先介绍一下斐波那契数列:1、1、2、3、5、8、13、21、34、55……
在数学上,斐波那契数列以递推的方法定义:F(0)=0,F(1)=1, F(n)=F(n - 1)+F(n - 2)(n ≥ 2,n ∈ N*)
代码的实现:
/*斐波那契数列第n项*/
int fibonacci(int n){
/*返回数列第n项,当n>2时,递归利用递推关系算出第n项*/
return (n==1||n==2)?1:fibonacci(n-1)+fibonacci(n-2);
}
int main(){
int n,fn;
while(1){
int sum = 0;
printf("输入项数/(q->exit):");
scanf("%d",&n);
if(getchar()=='q')
break;
for(int i = 1;i <= n;i++){
fn = fibonacci(i);
sum += fn; /*不建议求和项数太多,因为数列越往后数值会变得非常大,求和会容易溢出(参考下图的代码测试)*/
printf("%d ",fn);
}
printf("n前%d项和 = %dn",n,sum);
}
return 0;
}
Ubuntu20.04编译运行测试:
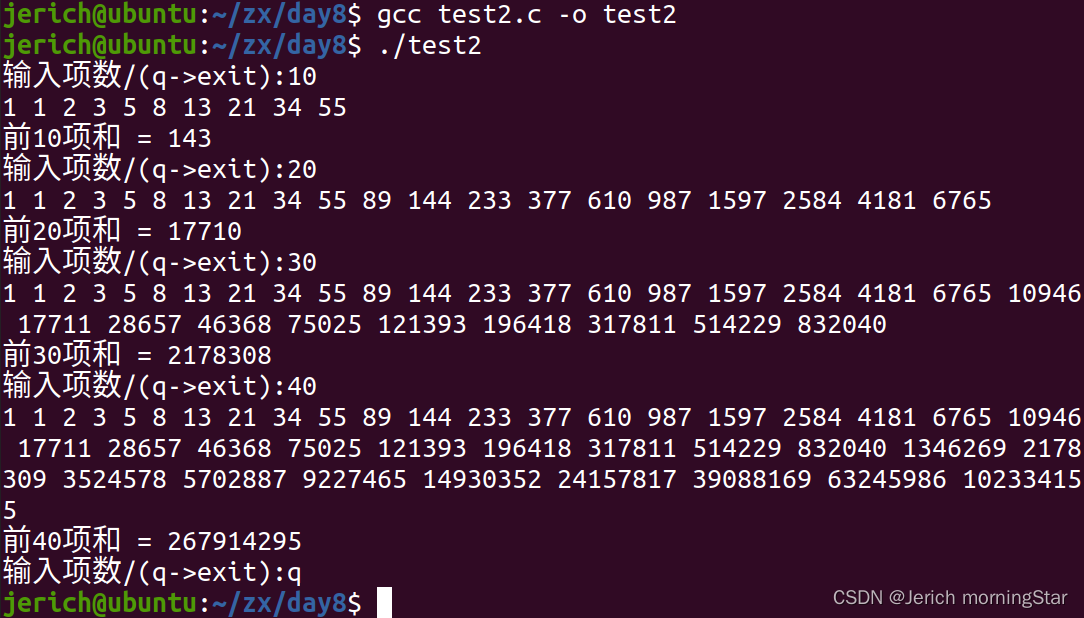
[8]输出二维数组中最大元素以及它的索引
思路:先遍历找出最大元素,再遍历每个元素与最大值比较等于就输出它的值以及索引。
代码的实现:
#include <stdio.h>
#include <stdlib.h>
int main(){
int arr[3][4];
for(int i = 0;i < 3;i++){
for(int j = 0;j < 4;j++){
arr[i][j] = rand()%30 + 1;
}
}
arr[0][3] =28; /*测试有多个相同最大值*/
for(int i = 0;i < 3;i++){
for(int j = 0;j < 4;j++){
printf("%dt",arr[i][j]);
}
putchar('n');
}
int maxVal = arr[0][0];
int maxIndex1 = 0;
int maxIndex2 = 0;
/*找出最大的元素*/
for(int i = 0;i < 3;i++){
for(int j = 0;j < 4;j++){
if(arr[i][j] > maxVal){
maxIndex1 = i;
maxIndex2 = j;
maxVal = arr[i][j];
}
}
}
/*判断有多个相同最大值*/
for(int i = 0;i < 3;i++){
for(int j = 0;j < 4;j++){
if(arr[i][j] == maxVal){
maxIndex1 = i;
maxIndex2 = j;
maxVal = arr[i][j];
printf("最大元素:arr[%d][%d] = %dn",maxIndex1,maxIndex2,maxVal);
}
}
}
return 0;
}
[9]冒泡排序(bubble sort)
排序思路:每次循环把最大的元素放到数组的最后面(排序皆是从小到大)。
代码的实现:
int temp;
bool flag = false;
for (int i = 0;i < N-1;i++){
/*每次内循环结束把最大的数放到后面N-i-1位置,保证数据从小到大排序*/
for(int j = 0;j < N-i-1;j++){
/*前者大则与后者交换,之后再与后面的值比较*/
if(arr[j] > arr[j+1]){
temp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = temp;
/*发生交换则true值给flag*/
flag = true;
}
}
/*每次排序结束判断,flag值是否发生变化,无变化说明数组已经有序,提前结束循环,节省时间*/
if(!flag){
break;
}else{
flag = false;
}
}
flag的作用:flag是对冒泡排序算法的优化,每次内循环结束都会将长度为N-i-1数组中最大的元素交换到最后面,当内循环结束没有发生数据的交换,说明数组已经是有序的了,此时flag=false,退出循环。
[10]杨辉三角
思路:
第一种:利用二维数组;
第二种:利用了它的排列组合的性质:第n行的第m个数可表示为 C(n-1,m-1),即为从n-1个不同元素中取m-1个元素的组合数。
二维数组方法的代码实现:
#include <stdio.h>
/*二维数组法*/
int main(){
int n;
printf("输入行数:");
scanf("%d",&n);
/*杨辉三角n行有n个元素*/
int arr[n][n];
/*三角形两条腰上元素都是1*/
for(int i = 0;i < n;i++){
arr[i][0] = arr[i][i] = 1;
}
/*每行从第二个元素开始,都是上一行前一个元素和后一个元素之和*/
for(int i = 2;i < n;i++){
for(int j = 1;j < i;j++){
arr[i][j] = arr[i-1][j-1] + arr[i-1][j];
}
}
/*打印三角形*/
for(int i = 0;i < n;i++){
/*三角形左边的空格*/
for(int j = 0;j < n-i;j++){
printf(" ");
}
/*跟在空格后打印每行的元素*/
for(int k = 0;k < i+1;k++){
printf("%6d",arr[i][k]);
}
putchar('n');
}
return 0;
}
排列组合法代码的实现:
#include <stdio.h>
/*阶乘*/
long int factorial(int a){
long int p=1;
for(int i = 1;i <= a;i++){
p *= i;
}
return p;
}
/*组合C(n,m),n为下标,m为上标*/
int Cn(int n,int m){
if(m == 1){
return 1;
}
else{
return factorial(n-1)/(factorial(m-1)*factorial(n-m));
}
}
/*杨辉三角*/
int main(){
int n;
printf("输入行数(1~20):");
scanf("%d",&n);
for(int i = 1;i <= n;i++){
for(int j = 0;j < n-i;j++){
printf(" ");
}
for(int k = 0;k < i;k++){
printf("%6d",Cn(i,k+1));
}
putchar('n');
}
return 0;
}
运行结果:
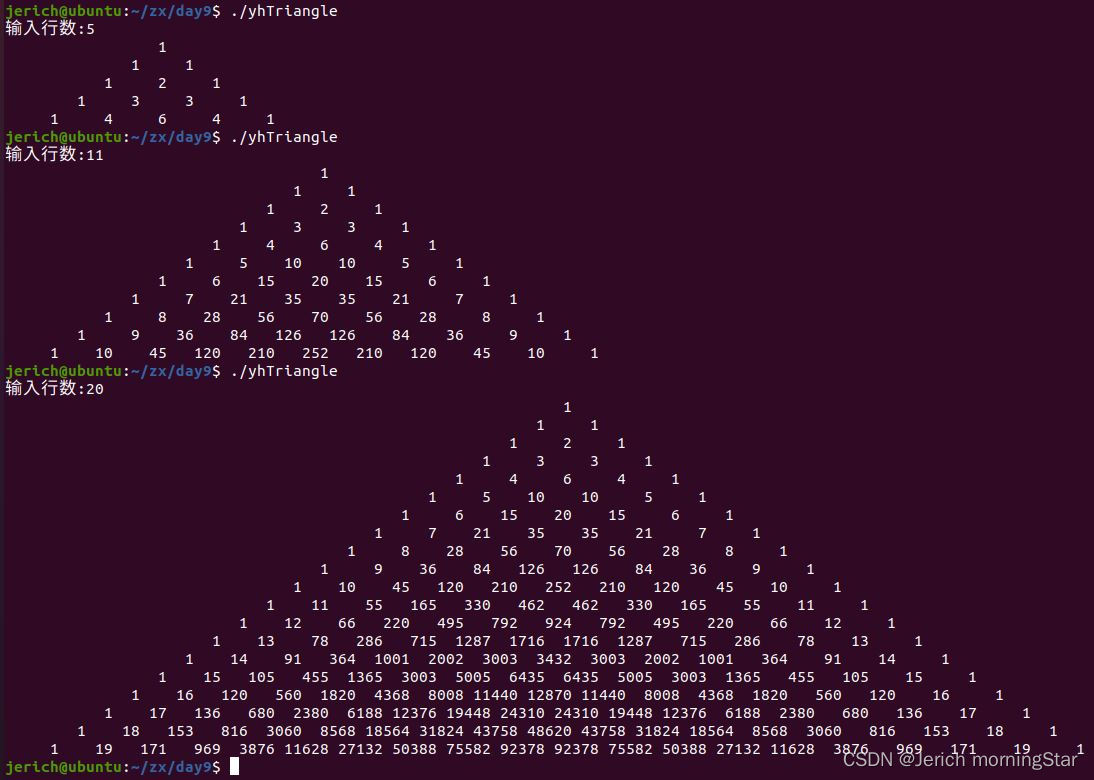
[11]约瑟夫环
使用数组法解决约瑟夫环问题
约瑟夫入狱,监狱内共有33个犯人。某日33名犯人围成一圈,从第一个犯人开始报数,报到数字7的犯人出列,被枪毙,
下一名犯人重新从1开始报数。依次类推,直至剩下最后1名犯人可被赦免。聪明的约瑟夫在心里稍加计算,算出了最后枪毙的位置,他站在这个位置,最终避免了自己被枪毙,逃出升天。
问:约瑟夫算出的是哪个位置?
- 提示:对于约瑟夫环问题来说,需要解决3个问题
- 如何解决数组循环的问题?
- 如何解决“逢7一杀”这个逻辑?
- 如何处理“已死之人”?
代码的实现:
#include <stdio.h>
#define N 33
#define KILL 7
int main(){
/*定义犯人数组,全部元素置零表示没被噶*/
int prisoner[N] = {0};
/*记录被噶了几个犯人*/
int counter = 0;
/*数组索引*/
int index = 0;
/*报数*/
int num = 0;
/*有一个辛存者,所以被噶了32个犯人时结束循环*/
while(counter != N-1){
/*如果数组索引=33,则置零再继续*/
if(index == N){
index = 0;
}
/*值为0 ,说明还没噶,要继续报数*/
if(prisoner[index] == 0){
num++;
/*报到7的人,噶了*/
if(num == KILL){
prisoner[index] = 1;
/*被嘎人数+1*/
counter++;
/*有人被噶,重新从1开始报数*/
num = 0;
printf("第%2d轮报数,%2d号位置的人被嘎了n",counter,index+1);
}
}
index++;
}
/*循环结束,遍历数组,看看约瑟夫站哪了*/
for(int i = 0;i < N;i++){
if(prisoner[i] == 0){
printf("约瑟夫在第%d个位置n",i+1);
}
}
return 0;
}
运行结果:
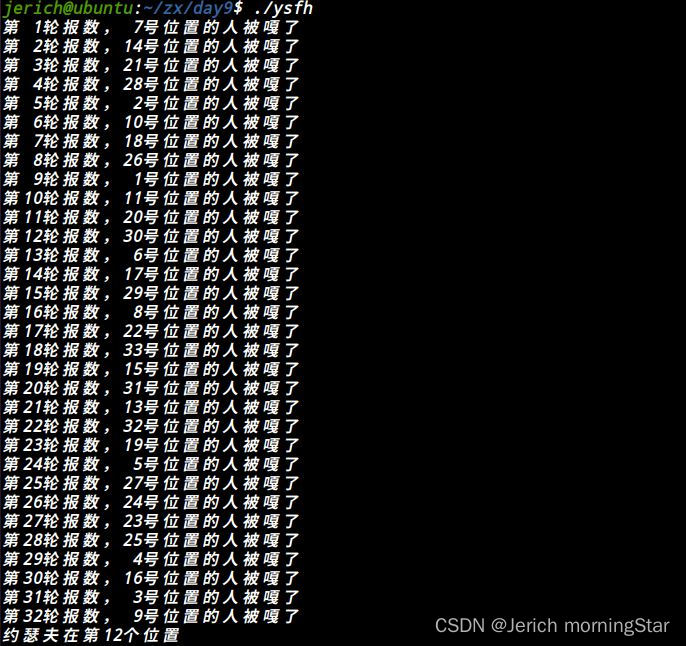
最后
以上就是缥缈音响最近收集整理的关于Linux及C基础学习总结的全部内容,更多相关Linux及C基础学习总结内容请搜索靠谱客的其他文章。








发表评论 取消回复