第十章重积分1. 曲顶柱体的体积：2.平面薄片的质量：3.二重积分的定义：5.直角坐标中二重积分的计算（最基本的方法）6.三重积分：7.重积分的应用：

66 阅读 0 评论 44 点赞

我是靠谱客的博主糊涂香氛，最近开发中收集的这篇文章主要介绍第十章重积分1. 曲顶柱体的体积：2.平面薄片的质量：3.二重积分的定义：5.直角坐标中二重积分的计算（最基本的方法）6.三重积分：7.重积分的应用：，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

1. 曲顶柱体的体积：

规则柱体的体积公式： $tiny V= Sh$ .

想象在曲顶柱体的底面上任取一小块区域，记作： $tiny dsigma$ （这一小块的面积也用 $tiny dsigma$ 来表示），设曲顶柱体的顶面有函数 $tiny z=z(x,y)$ ,取小闭区域上任一点作为小柱体的高，则小柱体的体积近视表示为 $tiny zd sigma$ ,取积分就得到柱体的体积

2.平面薄片的质量：

质量元素为： $tiny u(x,y) dsigma$

3.二重积分的定义：

$tiny iint_{D} f(x,y)dsigma = lim_{ lambda to 0} sum_{i=1}^{n}f(xi_i,eta_i)Delta sigma_i =iint_{D} f(x,y)dxdy$

1. 函数 $tiny f(x,y )$ 是定义在有界闭区域上D上的

2.函数 $tiny f(x,y )$ 是有界函数。

3.对积分区域的划分是用直线网来划分的。

4.结论：有界闭区域D上的连续函数 $tiny f(x,y )$ 的二重积分必定存在，即是定义中的极限必定存在。

5.曲顶柱体的体积：

$tiny V= iint_{D}f(x,y)dxdy$

平面包边的质量：

$tiny m= iint_{D}u(x,y)dxdy$ ，其中u（x，y）是薄片的面密度，所谓薄片就是单位厚度，理解为各种“1” ，例如：1CM,1M根据实际选取的量纲不同而不同。

6.二重积分的几何意义：曲顶柱体的体积， $tiny f(x,y )$ 是曲顶柱体的顶在点 $tiny (x,y )$ 处的竖坐标。

6.1 如果 $tiny f(x,y ) < 0$ ，那么 $tiny V< 0$ ;

6.2 如果 $tiny f(x,y ) > 0$ ，那么 $tiny V> 0$ ;

6.3 如果（f 有正有负）

$tiny left{begin{matrix} f(x,y ) > 0,(x,y) in D_1\ \ f(x,y ) < 0,(x,y) in D_2 \ .....\D=D_1+D_2+... end{matrix}right. Rightarrow V=V_1+V_2+....$

6.4当二重积分的最大值

$tiny left{begin{matrix} V_{max}=iint_{D_1 in D }f(x,y)dxdy\ \ D_1=left { (x,y)|f(x,y)>0 right } end{matrix}right.$

4.二重积分的性质：

4.1 函数可加（积分区域相同函数可以相加减）

4.2 积分区域可加，（函数相同，不同的积分区域可以相加减，这个可以结合初等数学中的所谓“割补法”）

4.3 二重积分可以计算闭区域的面积

$tiny S_D=iint_{D}dxdy= iint_{D}1.dxdy$

====不等性质：

4.4 若

$tiny f(x,y) leq g(x,y) Rightarrow iint_Df(x,y)dxdy leq iint_Dg(x,y)dxdy$ .

事实上 $tiny g-fgeq 0$

绝对值不等式：

   $tiny left | iint_Df(x,y)dxdy right | leq iint_D left | f(x,y) right | dxdy$

4.5 估值不等式

   $tiny msigma leq iint_Df(x,y)dxdy leq Msigma$

4.6 中值定理：

   $tiny iint_Df(x,y)dxdy =f(xi,eta)sigma$

============二重积分的计算

5.直角坐标中二重积分的计算（最基本的方法）

5.1 后积先定限，限内画条线，从负向着正，先交为下限，后交为上限。

$tiny iint_{D}f(x,y)dsigma =int_{a}^{b}dxint_{y_1(x)}^{y_2(x)}f(x,y)dy ,(y_1(x)leq y leq y_2(x),aleq xleq b)$

TIP：根据积分区域的类型，选择合适的积分次序：

（1）转化成定积分容易计算；

（2）积分区间容易表达，计算量低。

（3）利用积分区间的对称性，配合积分的集合意义；和被积函数的奇偶性事先化简积分。

==============

待补充

==============

5.2 利用极坐标计算：

极坐标于直角坐标的关系：

$tiny left{begin{matrix} r^2=x^2+y^2\ \ x=rcostheta \ y=rsintheta end{matrix}right.$

极坐标下的面积元素：

$tiny dsigma = rdrdtheta Rightarrow S = iint_Drdrdtheta$

利用极坐标做代换之后，二重积分的计算仍然按照直角坐标的计算方式进行；重点在于极坐标下积分区域的表示。

5.3 二重积分的换元法：

$tiny iint_Df(x,y)dxdy = iint_{D'}f[x(u,v),y(u,v)]J(u,v)duddv$

（1）换元法是坐标面的变换，极坐标变化，可以看作是换元法的特殊情形；

（2）主要是各种整体代换。

（3）要求 $tiny x(u,v),y(u,v)$ 具有一阶连续偏导数，保证代换后仍然可积；雅克比行列式不为零；映射是一对一的；

6.三重积分：

6.1 三重积分是二重积分的推广,实际意义是空间几何体的质量。

6.2 定义：

$tiny iiint_Df(x,y,z)dxdydz =lim_{lambda to 0} sum_{i=0}^{n}f(xi_i,eta_i,zeta _i) Delta v_i =iiint_Df(x,y,z)dv$

6.3 三重积分的计算：

$tiny iiint_Df(x,y,z)dxdydz =$

（1）投影法：先1后2；后积先定限，限内画条线；

（2）截痕法：先2后1；后积先定限，限内画个面

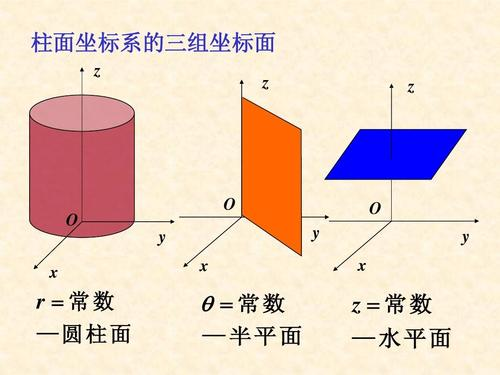
6.4 柱面坐标计算三重积分:

柱面坐标：

$tiny left{begin{matrix} 0 leq r leq infty \ 0leq theta leq 2pi \ -infty leq z leqslant +infty \ end{matrix}right. Rightarrow x=rcostheta ,y =rsintheta ,z=z$

r为常数，表示以z为轴的柱面； $tiny theta$ 为常数表示过z轴的半平面；z为常数表示平行于 $tiny xoy$ 面的平面

柱面坐标下的的体积元素：

$tiny dv=rdrdtheta dz$

柱面坐标下的三重积分：

$tiny iiint_{mho }f(x,y,z)dxdydz = iiint_{mho }f(rcostheta,rsintheta,z)rdrdtheta dz$ （投影在xoy面的情形，类似可以讨论投影到其他坐标面的情形）

球面坐标计算三重积分：

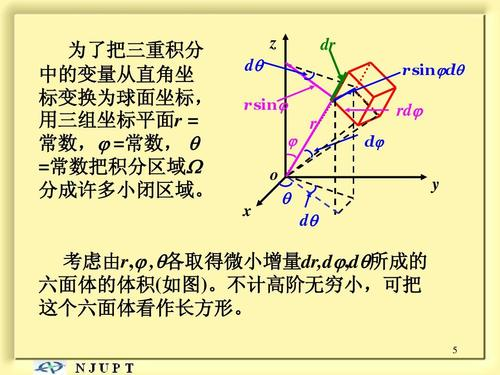
纬线的微分是先计算近似点处的平面半径，然后根据弧长公式取得角度增量 $tiny dtheta$ ,

因此， $tiny dv= dr . rdvarphi .rsinvarphi d theta$

$tiny iiint_{mho }f(x,y,z)dxdydz = iiint_{mho }f(rsin varphi costheta,rsinvarphi sintheta,rcosvarphi)r^2sinvarphi drdtheta dvarphi$

7.重积分的应用：

曲面的面积：

空间平面在坐标面上上投影区域的面积

$tiny d sigma = cos gamma dS$

$tiny cos gamma = frac{1}{sqrt{1+z_x^2+z_y^2}}$

于是空间曲面的面积为：

$tiny iint_{D_{xy}}sqrt{1+z_x^2+z_y^2}dxdy =A$

注意：空间曲面的法向量公式。

质心：

质点的静矩：md ，利用元素法求得总的静矩于物体的质量做比值就得到质心坐标。

密度均匀薄片的质心公式：

$tiny overline{x} =frac{1}{A}iint_Dxdsigma, overline{y} =frac{1}{A}iint_Dydsigma,$ 由于这时候的质心，只与薄片的集合形状相关，所以也叫做形心

转动惯量：

质点的转动惯量： $small Md^2$

平面薄片的转动惯量：

$tiny I_x=iint_Dx^2u(x,y)dsigma,I_y=iint_Dy^2u(x,y)dsigma$

万有引力：

量个质点的万有引力公式：

$tiny F=Gfrac{m_1m_2}{r^2}$

利用元素法，可以表示出近似质点的引力，然后再分解到各个坐标方向上在积分，就得到各个方向上的分力；

记住：空间向量的方向余弦的计算