马尔科夫矩阵

# Author:Wyy
# -*- coding = utf-8 -*-
# @Time :2022/11/14 
# @Author:WYY
# @Site :
# @File :马尔科夫链模型状态转移矩阵.py
# @Software: PyCharm
import numpy as np
matrix = np.matrix([[0.9,0.075,0.025],[0.15,0.8,0.05],[0.25,0.25,0.5]], dtype=float)# 马尔科夫链模型的状态转移矩阵
vector1 = np.matrix([[0.3,0.4,0.3]], dtype=float)# 假设我们当前股市的概率分布为：[0.3,0.4,0.3]
for i in range(100):# vector1作为序列概率分布的初始状态t0，将其带入这个状态转移矩阵计算t1,t2,t3...的状态
    vector1 = vector1*matrix
    print("Current round:", i+1)
    print(vector1)

# 更换一个初始概率分布
matrix = np.matrix([[0.9,0.075,0.025],[0.15,0.8,0.05],[0.25,0.25,0.5]], dtype=float)
vector1 = np.matrix([[0.7,0.1,0.2]], dtype=float)# 假设当前股市的概率分布为[0.7,0.1,0.2]
for i in range(100):# 带入矩阵计算t1、2、3的状态
    vector1 = vector1*matrix
    print("Current round:" , i+1)
    print(vector1)

# 尝试证明对于一个确定的状态转移矩阵P，它的n次幂Pn在当n大于一定的值的时候也可以发现是确定的
matrix = np.matrix([[0.9,0.075,0.025],[0.15,0.8,0.05],[0.25,0.25,0.5]], dtype=float)
for i in range(10):
    matrix = matrix*matrix
    print("Current round:" , i+1)
    print(matrix)

输出结果：

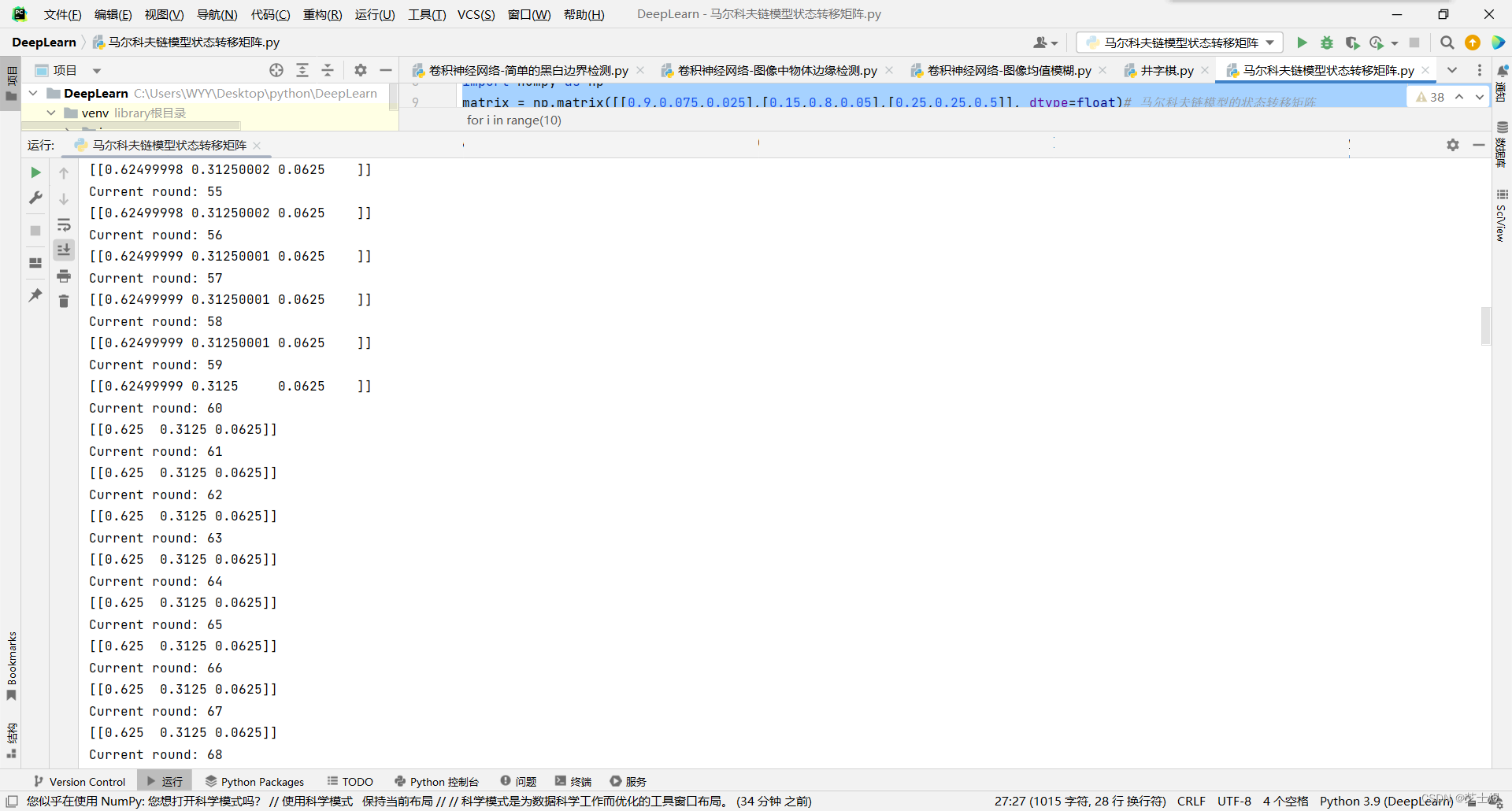
可以发现，从第60轮开始，我们的状态概率分布就不变了，一直保持在[0.625   0.3125  0.0625]，即62.5%的牛市，31.25%的熊市与6.25%的横盘。 

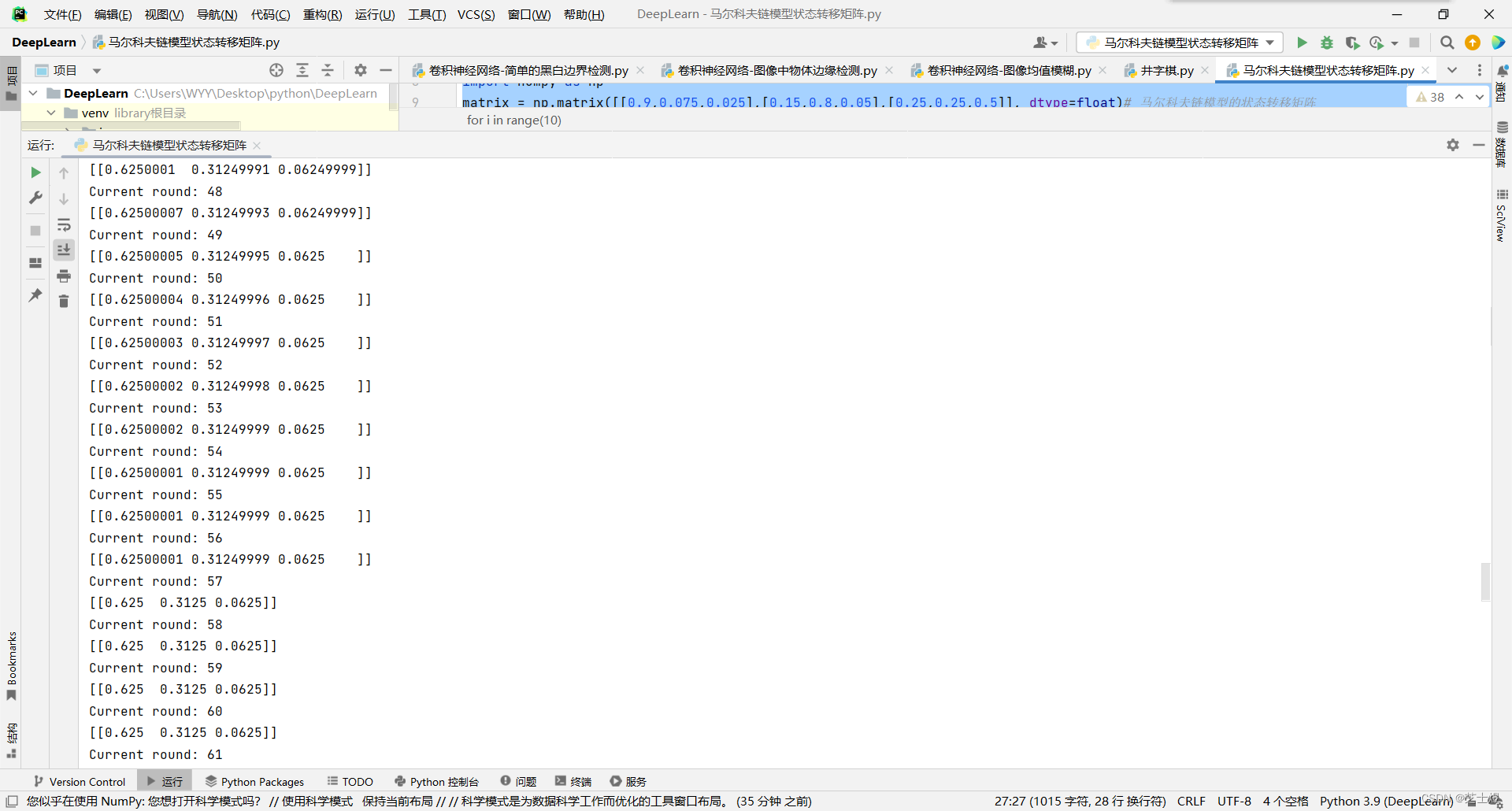
可以看出最终状态的概率分布趋于同一个稳定的概率分布[0.625   0.3125  0.0625]

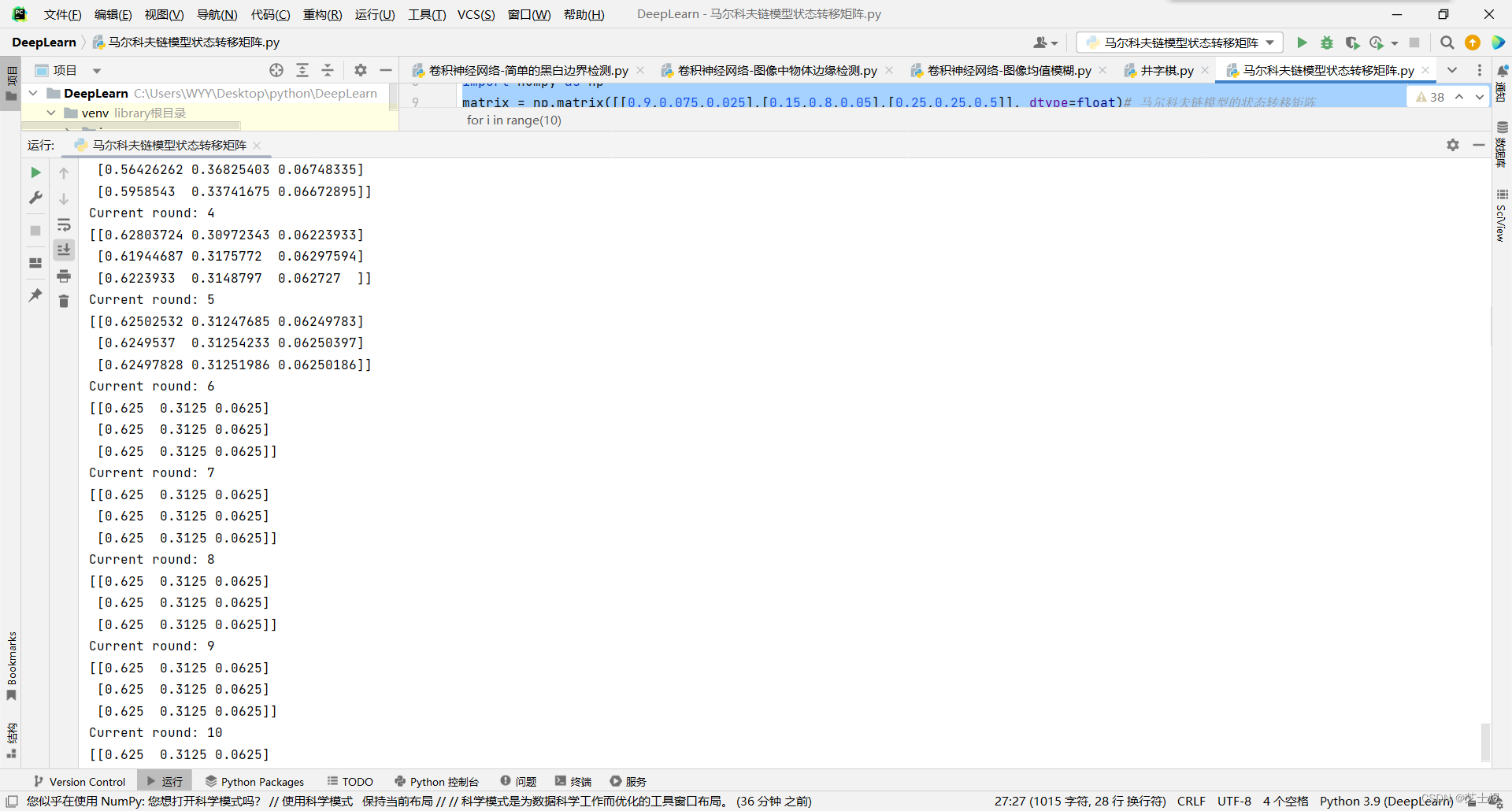
可以发现在n≥6n≥6以后，PnPn的值稳定不再变化，而且每一行都为[0.625   0.3125  0.0625]，这和我们前面的稳定分布一致。

最后

以上就是俊逸胡萝卜为你收集整理的马尔科夫矩阵的全部内容，希望文章能够帮你解决马尔科夫矩阵所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。