自然二进制码与格雷码相互转换

86 阅读 0 评论 57 点赞

我是靠谱客的博主聪明柠檬，最近开发中收集的这篇文章主要介绍自然二进制码与格雷码相互转换，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

自然二进制码与格雷码相互转换

一、格雷码简介

格雷码是由弗兰克·格雷于1953年发明，其主要特点是相邻编码值中间只有一个比特发生改变，又被称为循环码。

格雷码是一种无权码，采用绝对编码方式，典型格雷码是一种具有反射特性和循环特性的单步自补码，它在任意两个相邻的数之间转换时，只有一个数位发生变化。它大大地减少了由一个状态到下一个状态时逻辑的混淆。

二、自然二进制码转换为格雷码

自然二进制码转换成二进制格雷码，其法则是保留自然二进制码的最高位作为格雷码的最高位，而次高位格雷码为二进制码的高位与次高位相异或，格雷码其余各位依次求之。

原理: 
若二进制码表示为: B[N-1]B[N-2]...B[2]B[1]B[0]，
则二进制格雷码表示为: G[N-1]G[N-2]...G[2]G[1]G[0]。
其中最高位保留: G[N-1] = B[N-1]，
其他各位: G[i] = B[i+1] xor B[i]. (i = 0, 1, 2, ..., n-2)。

图示如下：

在这里插入图片描述
代码如下：

module b_to_g(binary,gray);
	
	parameter PTR = 8;   //设置位数
	
	input  [PTR-1:0] binary;
	output [PTR-1:0] gray;
	
	reg [PTR-1:0] gray;
	integer i;
	
	always @(*) begin
		for (i=0; i<PTR-1; i=i+1)
			begin 
				gray[i] = binary[i] ^ binary[i+1]; 
			end
		gray[PTR-1] = binary[PTR-1];
	end
	
endmodule

测试代码如下:

//b_to_g_tb

`timescale 1 ns/ 1ns

module b_to_g_tb();
  
    parameter PTR = 8;
	reg  [PTR-1:0] binary;
	wire [PTR-1:0] gray;
	
	integer i;
	
	b_to_g my_b_to_g(
		.binary(binary),
		.gray(gray));
		
	initial
	begin
		binary = 0;
		#2 for(i=0;i<20;i=i+1)
			begin
				#2 binary = $random;
			end
	end
	
endmodule

仿真波形如下（清晰显示请点开放大）：

在这里插入图片描述

三、格雷码转换为自然二进制码

二进制格雷码转换成自然二进制码，其法则是保留格雷码的最高位作为自然二进制码的最高位，而次高位自然二进制码为高位自然二进制码与次高位格雷码相异或，而自然二进制码的其余各位依次求之。

原理: 
若二进制格雷码表示为: G[N-1]G[N-2]...G[2]G[1]G[0]，
则二进制码表示为: B[N-1]B[N-2]...B[2]B[1]B[0]。
其中最高位保留: B[N-1] = G[N-1];
其他各位: B[i-1] = G[i-1] xor B[i]. (i = 1, 2, ..., n-1)。

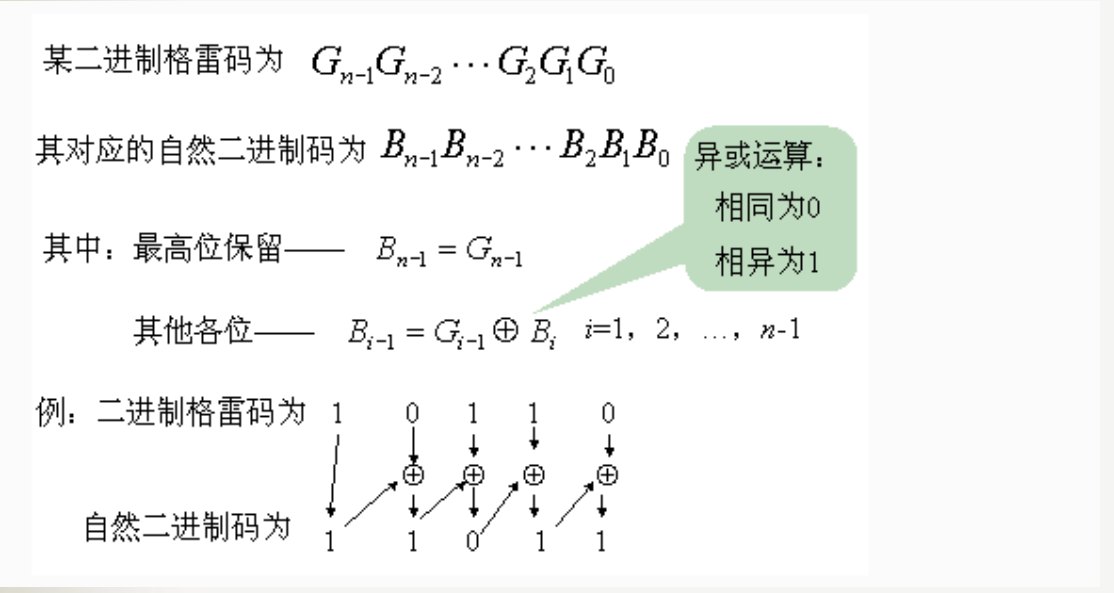
图示如下：

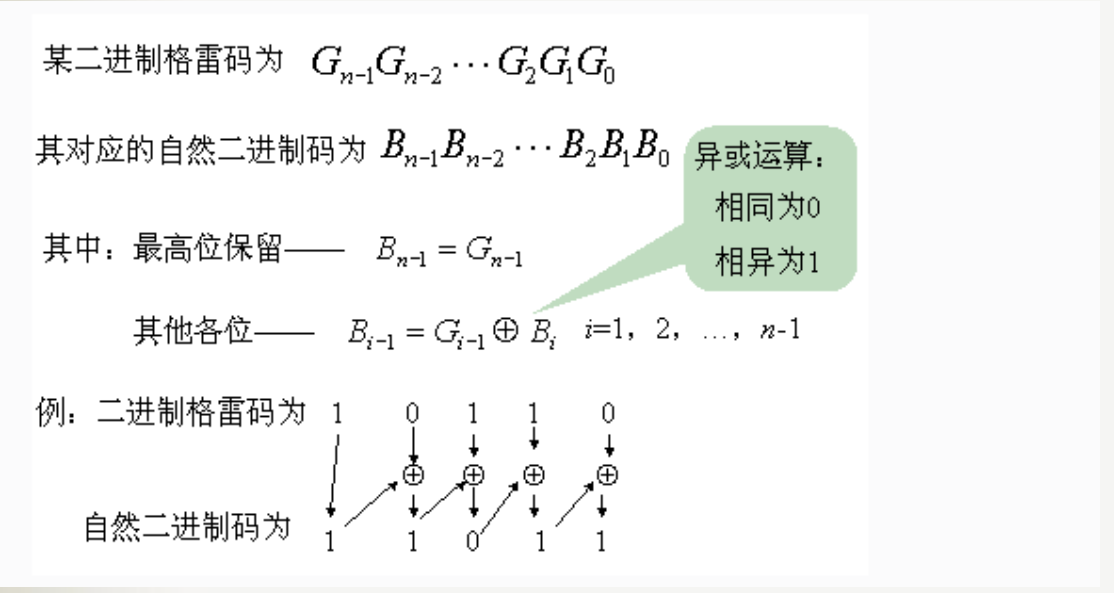
在这里插入图片描述
代码如下：

module g_to_b (
  binary, gray);
   
  parameter PTR = 8;
  input  [PTR-1:0] gray;
  output [PTR-1:0] binary;
  
  integer i;
  reg [PTR-1:0] binary;
  
  always @(*) begin
 	 //这里我用for (i=0; i<PTR-1; i=i+1)的话，仿真结果不对。
 	 //不大清楚，有明白的同学请指出。
    for (i=PTR-2; i>=0; i=i-1)  
      begin
        binary[i] = binary[i+1] ^ gray[i];
      end
      binary[PTR-1] = gray[PTR-1];
  end
  
endmodule

测试代码如下:

//g_to_b_tb

`timescale 1 ns/1 ns

module g_to_b_tb();
  
  parameter PTR = 8;
  integer i;
  
  reg   [PTR-1:0] gray;
  wire  [PTR-1:0] binary;
  
  g_to_b my_g_to_b(
 	 .gray(gray),
 	 .binary(binary)
	  );
  
  initial
  begin
    gray = 0;
    #2 for (i=0; i<30; i=i+1)
        begin
          #2 gray = $random;
        end
  end
  
endmodule

仿真波形如下（清晰显示请点开放大）：

在这里插入图片描述