1、主成分分析
(1)用途
- 非监督的机器学习算法
- 主要用于数据的降维
- 通过降维,可以得到更容易理解的特征信息
- 可以方便数据可视化、用于去噪
(2)原理
坐标系上有五个点,需要通过降维,在最大程度保留数据信息的基础上将二维表示的数据降到一维。所以我们需要找到一个轴,使得样本映射到轴上之后,样本间的方差最大(最容易区别各个样本)
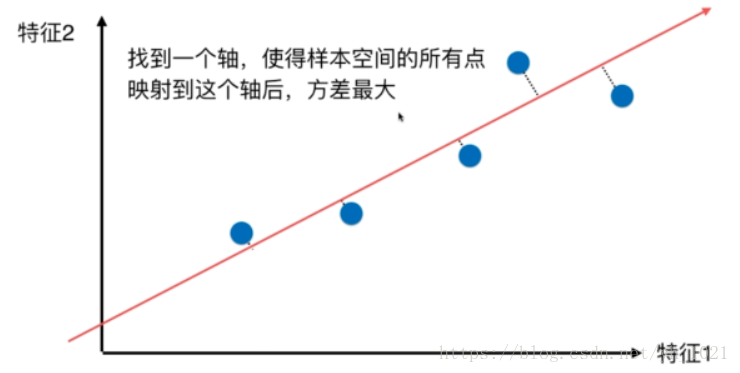
。需要求一个轴的方向w=(w1,w2),使得所有样本映射到w以后,方差最大,
即
Var(x)=1m∑mi=1∥xi∥2
V
a
r
(
x
)
=
1
m
∑
i
=
1
m
‖
x
i
‖
2
的值最大,
xi
x
i
是映射到w轴后的坐标值。

2、用梯度上升法求解第一主成分
目标:求w,使得
f(x)=1m∑mi=1(x(i)1w1+x(i)2w2+...+x(i)nwn)2
f
(
x
)
=
1
m
∑
i
=
1
m
(
x
1
(
i
)
w
1
+
x
2
(
i
)
w
2
+
.
.
.
+
x
n
(
i
)
w
n
)
2
最大
向量化梯度表达式:
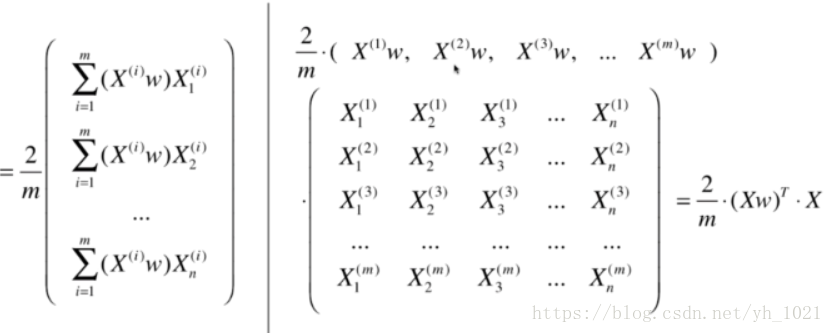
x的下标表示第几个特征,上标表示第几个样本,最终得到目标函数梯度的表达式
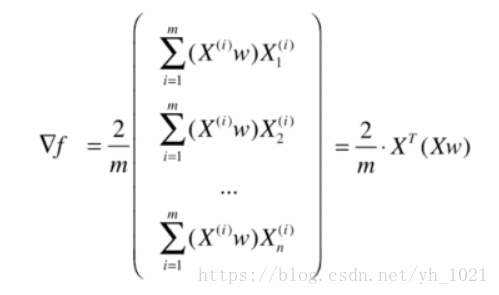
import numpy as np
import matplotlib.pyplot as plt
X = np.empty((100,2)) #X具有两个特征
X[:,0]=np.random.uniform(0.,100.,size=100) #0-100之间进行随机分布
X[:,1]=0.75*X[:,0]+3.+np.random.normal(0.,10.,size=100)
plt.scatter(X[:,0],X[:,1])
plt.show()
#将样本均值归零
def demean(x):
return x-np.mean(x,axis=0) #在行方向上求均值,即对每一列求均值
x_demean=demean(X)
###############梯度上升法##################
#目标函数
def f(w,x):
return np.sum((X.dot(w)**2))/len(X)
#目标函数梯度:
def df(w,x):
return X.T.dot(X.dot(w))*2./len(X)
#梯度上升法
#因为w为单位向量,但是每一次梯度上升后不一定为单位向量,所以需要化为单位向量的函数
def direction(w):
return w/np.linalg.norm(w)
def gradient_descent(X,w,eta,n_iters=1e4,epsilon=1e-8):
cur_iter=0
while cur_iter<n_iters:
gradient=df(w,X)
last_w=w
w=w+eta*gradient
w=direction(w)
if(abs(f(last_w,X)-f(w,X))<epsilon):
break
cur_iter+=1
return w
initial_w=np.random.random(X.shape[1]) #初始时w不能全为0,不然之后都为0
eta=0.001
#不能使用standardscalar标准化数据,因为目标函数要求方差最大化,若标准化数据后,样本方差就为1,也就没有最大方差了
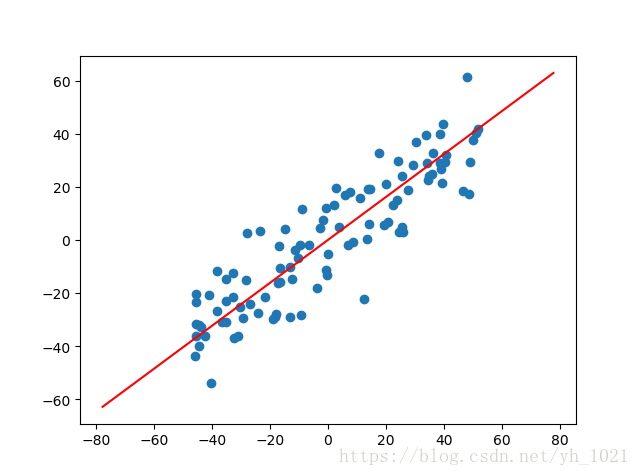
w=gradient_descent(x_demean,initial_w,eta)
print(w)
plt.scatter(x_demean[:,0],x_demean[:,1])
plt.plot([-w[0]*100,w[0]*100],[-w[1]*100,w[1]*100],color='r')
plt.show()要使均值为0,但因为目标函数是求方差的最大值,所以不能通过归一化样本使方差为1。
最后通过梯度下降法可以得到w轴的方向
3、求解数据的前n个主成分

将投影在第一主成分轴上的长度再乘以单位向量w,即可以得到数据在第一主成分方向上的向量,若将数据在第一主成分上的分量去掉,可以得到新数据
X′(i)
X
′
(
i
)
,在新的数据上面求第一主成分,就可以得到第二主成分,以此类推可以得到前n个主成分。
在sklearn中的PCA:
from sklearn import datasets
digits=datasets.load_digits()
X=digits.data
Y=digits.target
from sklearn.model_selection import train_test_split
x_train,x_test,y_train,y_test =train_test_split(X,Y,random_state=666)
from sklearn.neighbors import KNeighborsClassifier
knn=KNeighborsClassifier()
knn.fit(x_train,y_train)
result1= knn.score(x_test,y_test)
print(result1)
########使用PCA降维######################
from sklearn.decomposition import PCA
pca=PCA(n_components=2) #保留前两个最大的主成分
pca.fit(x_train)
#用训练数据集训练得到的pca来得到训练和测试数据集的降维结果
x_train_reduction=pca.transform(x_train)
x_test_reduction=pca.transform(x_test)
knn_pca=KNeighborsClassifier()
knn_pca.fit(x_train_reduction,y_train)
result2=knn_pca.score(x_test_reduction,y_test)
print(result2)得到的结果分别为:
0.9866666666666667
0.6066666666666667可以看出使用PCA虽然可以节省时间,但是会损失很多精度。当然,保留的主成分数量越多,精度越高。在sklearn中可以使用pca中的explained_variance_ratio_方法,可以得到样本所有主成分所拥有信息量的比重。
pca=PCA(n_components=x_train.shape[1]) #得到样本的所有主成分
pca.fit(x_train)
pca.explained_variance_ratio_
#画出前i个成分的总和所占的比重
plt.plot([i for i in range(x_train.shape[1])],
[np.sum(pca.explained_variance_ratio_[:i+1]) for i in range(x_train.shape[1])])
plt.show()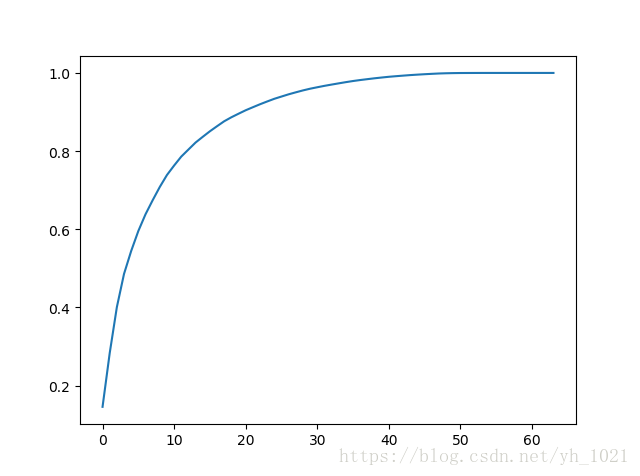
sklearn中也可以指定需要得到所有信息量的百分之多少的信息量所对应的主成分个数:
pca=PCA(0.95)
pca.fit(x_train)
print(pca.n_components_) #打印出拥有95%信息量的主成分的个数
#为28再使用此pca对数据进行降维,并用knn对此计算精确度:
x_train1=pca.transform(x_train)
x_test1=pca.transform(x_test)
knn=KNeighborsClassifier()
knn.fit(x_train1,y_train)
result=knn.score(x_test1,y_test)
print(result)
#结果为0.98步骤:
1、先确定需要保留的信息量,如95%,并用pca=PCA(0.95)得到此pca
2、再用此pca对训练集和数据集进行降维
3、用分类、回归模型计算精确度
优点:
尽可能的保留精确度的前提下提高了运算效率
若降维至二维,则可以进行可视化
pca=PCA(n_components=2)
pca.fit(x_train)
x_reduction=pca.transform(X)
for i in range(10):
plt.scatter(x_reduction[Y==i,0],x_reduction[Y==i,1],alpha=0.8)
plt.show()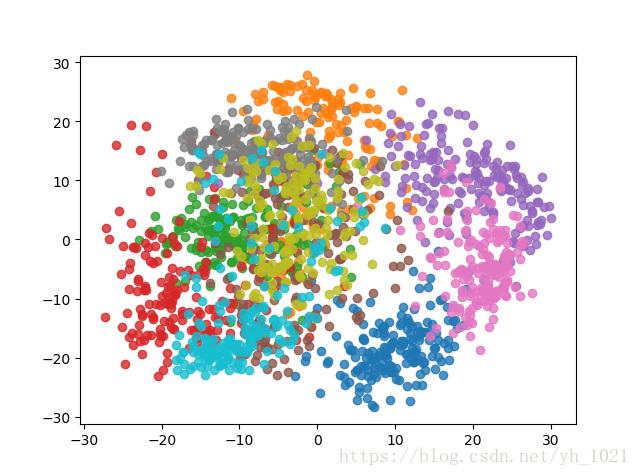
4、利用MNIST数据集验证PCA降维后的效果
import numpy as np
from sklearn.datasets import fetch_mldata #可以从官方网站中下载各种机器学习数据集
#加载手写数字数据集
mnist=fetch_mldata("MNIST original")
x,y=mnist['data'],mnist['target']
print(x.shape)
x_train=np.array(x[:60000],dtype=float)
y_train=np.array(y[:60000],dtype=float)
x_test=np.array(x[60000:],dtype=float)
y_test=np.array(y[60000:],dtype=float)
print(x_train.shape)
#使用KNN
from sklearn.neighbors import KNeighborsClassifier
#PCA降维
from sklearn.decomposition import PCA
pca=PCA(0.9) #降维后希望保持90%的信息量
pca.fit(x_train)
x_train_reduction=pca.transform(x_train)
print(x_train_reduction.shape)
knn_pca=KNeighborsClassifier()
knn_pca.fit(x_train_reduction,y_train)
x_test_reduction=pca.transform(x_test)
result=knn_pca.score(x_test_reduction,y_test)
print(result)(70000, 784)
(60000, 784)
(60000, 87)
0.9728准确率为97.28%,在提高效率的情况下,精度下降不是很明显。
5、使用PCA降噪
先通过PCA降维,将降维后的数据重建成原来维度的数据,就可以起到降噪的过程,原理还是通过PCA方法会丢失部分数据,只不过丢失的数据可能为噪声。
import numpy as np
import matplotlib.pyplot as plt
x=np.empty((100,2))
x[:,0]=np.random.uniform(0.,100.,size=100)
x[:,1]=0.75*x[:,0]+3.+np.random.normal(0,5,size=100)
plt.scatter(x[:,0],x[:,1])
plt.show()
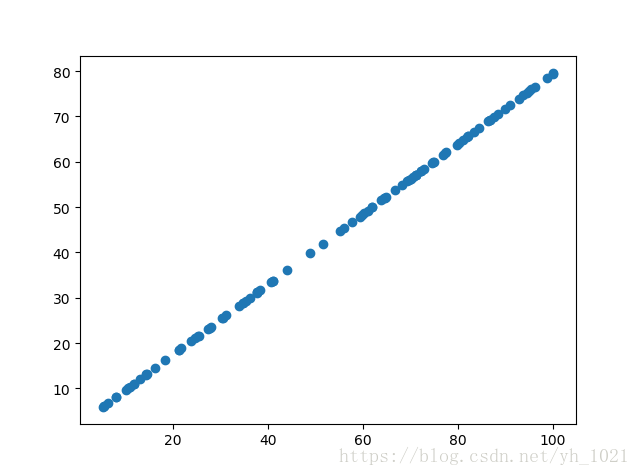
from sklearn.decomposition import PCA
pca=PCA(n_components=1)
pca.fit(x)
x_reduction=pca.transform(x)
x_restore=pca.inverse_transform(x_reduction) #将降到一维的数据重建成二维数据
plt.scatter(x_restore[:,0],x_restore[:,1])
plt.show()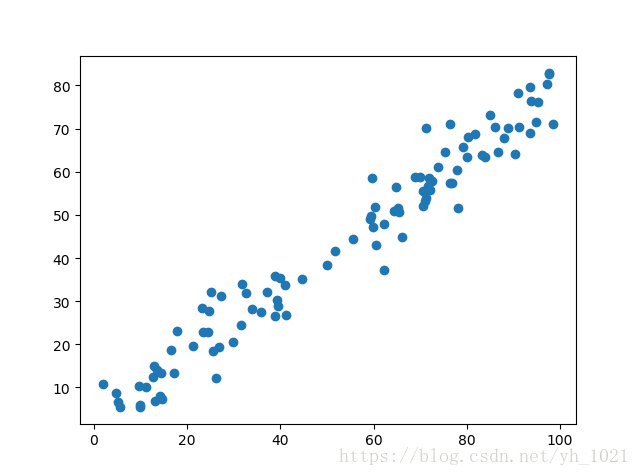
PCA降噪后
ps:可以使用from sklearn.datasets import fetch_lfw_people 尝试人脸识别
最后
以上就是呆萌白羊最近收集整理的关于主成分分析法(PCA)——自学第六篇的全部内容,更多相关主成分分析法(PCA)——自学第六篇内容请搜索靠谱客的其他文章。








发表评论 取消回复