首先,线性规划,比较简单,对误差方程 Ex = (y-mx-c)^2 分别求偏导,再令偏导等于0 一步一步的求出m和c。 令偏导等于0的原因是为了寻找极致点,我们假设每次迭代的都是极值点,而极值点的特点是导数为0。
python代码表示就是:
for i in np.arange(1000000):
m = ((y - c)*x).sum()/(x*x).sum()
c = (y-m*x).sum()/y.shape[0]
数据是老师给的,mc要提前赋值(找个差不多像的随机值,不然要迭代好多次)
这样迭代下来的结果就是:
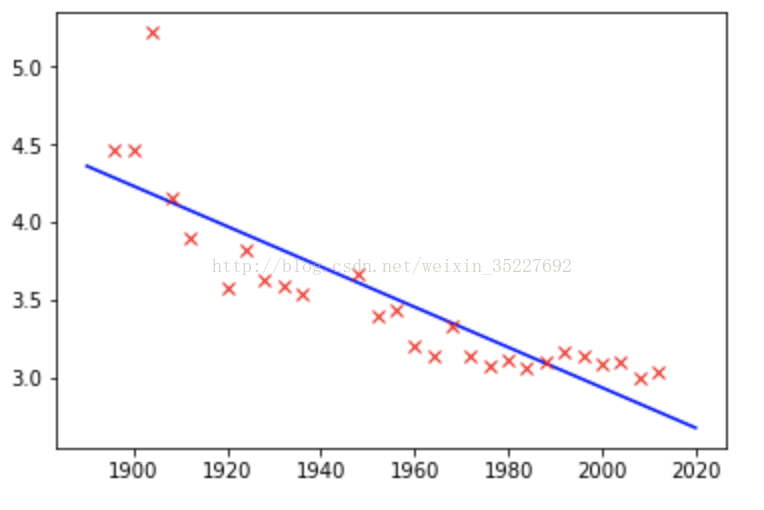
很明显,这些观测数据点是近似线性的,但是用线性规划不足以使误差达到很小的状态,所以现在的做法就是提高维度,用多个基础方程的形式表现,拟合出一个高维的空间模型,而这个模型我们用向量来表示,所以参数形式上还是线性的。

现在可以用代码生成一个多项式的方程:
def polynomial(x, degree, loc, scale):
degrees = np.arange(degree+1) Phi = ((x-loc)/scale)**degrees return Phi 这个东西算出来的返回值是:
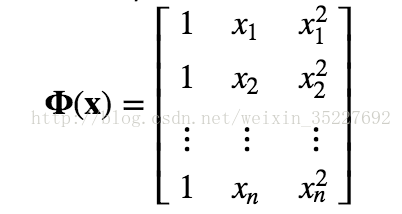
这个形式的。
按照最小二乘法找误差:
E(w)=(y−Xw)⊤(y−Xw)
求出偏导:
∂∂wE(w)=−2X⊤y+2X⊤Xw
之前的文章也有提及将偏导数 等于零的时候, 就是这个公式求得的极值(因为斜率为0 这个点是才是顶点或者谷点)
0=−2X⊤y+2X⊤Xw
求得
X⊤Xw=X⊤y
直接求这个公式的话,如果x的矩阵是特别大的 那么 x的转置矩阵 乘以 x 计算量会非常的大, 所以我们需要通过QR矩阵分解:(听说我们学校的教授 neil大神,对世界矩阵分解做出了一些贡献,。。现在个人拿到的研究经费已经有半个亿了,最近又被google 挖过去带一个新部门。。所以, 同学们 学好数学,,,,)
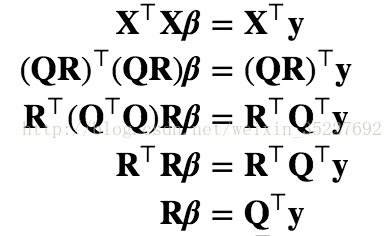
用代码表现就是:
def fit(Phi, y):
Q, R = np.linalg.qr(Phi)
w = sp.linalg.solve_triangular(R, np.dot(Q.T, y))
return w
拟合出来的w 还可以用来预测未来值,只要将预测的x带入上边的求Phi的方法内,再用这个w做向量点乘,然后把每一个基础方程的值加起来就好了(这里会在下边的完整代码中看到并且明白是怎么回事)
完整代码:
def quadratic(x):
Phi = np.ones((x.shape[0], 3))
Phi[:,1:2] = x
Phi[:,2:3] = x**2
return Phi
Phi = quadratic(x)
#下面这三行就是用三方库求得的 w
import scipy as sp
Q, R = np.linalg.qr(Phi)
w = sp.linalg.solve_triangular(R, np.dot(Q.T, y))
y_pred = (w.T*Phi)[:,0:1]+(w.T*Phi)[:,1:2]+(w.T*Phi)[:,2:3]
import pylab as plt
fig, ax = plt.subplots(figsize=(12,4))
ax.plot(x, y, 'rx')
ax.plot(x, y_pred, 'g-')
plt.title('the error')
结果是:
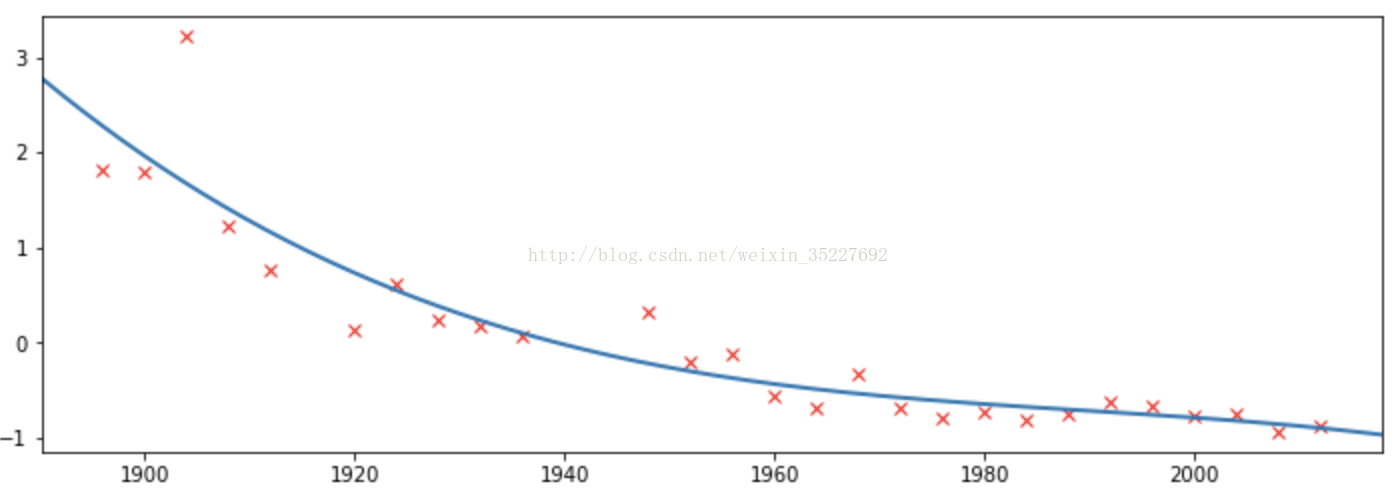
在此基础上,可以进行很多validation的验证,什么k-fold hold one out 什么的,这些很简单,下边lab作业我也全都写了,one out 那个 适合小数据量,k fold那个就是分组验证,防止过拟合这种,主要是为了模型拟合成功,用来预测的可靠性。
最后
以上就是妩媚百合最近收集整理的关于基于线性回归与核函数——linear function & basis function 的代码,处理马拉松数据的全部内容,更多相关基于线性回归与核函数——linear内容请搜索靠谱客的其他文章。








发表评论 取消回复