均匀分布产生高斯分布
- 简介
- 方法和证明
- 逆变换法
- Box-Muller算法
- 拒绝采样
- 代码
- 逆变换代码
- Box-Muller算法代码
- 拒绝采样代码
- 效果
- 检验
- 算法效果
- 引用
简介
上图像处理课的小作业，顺便复习概率论！！
这里只用了三种方法，未完待续。。。
方法和证明
已经写成word了，不想再打一遍了awsl。
逆变换法
Box-Muller算法
拒绝采样
代码
逆变换代码
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45clc; clear; % 验证高斯噪声-------------- ep = 1e-3; %间隔 x = -4 : ep : 4; num = length(x); U = rand(1, num); gaussian = @(u) sqrt(2) * erfinv(u); %高斯分布的逆累积分布函数 y = gaussian(2 * U - 1); [f, xi] = ksdensity(y, x); %绘制概率分布 % 作图 figure(1); plot(x, f); % 添加高斯噪声-------------- img = imread('lena.bmp'); Nvar = [0 50]; % 均值0，标准差50 rate = 0.5; % 50%的区域加噪声 img_processed = add_Guassian_noise(img, Nvar, rate); % 原图 figure(2); subplot(1, 2, 1); imshow(img); title('src'); % 处理后 subplot(1, 2, 2); imshow(img_processed); title('dst'); function dst = add_Guassian_noise(src, Nvar, rate) % src --> raw img to be processed % Nvar --> [mean, std] % rate --> the rate of noise [r, c] = size(src); src = double(src); flag = (rand(r,c) > rate); U = rand(r, c); noise = Nvar(2) * sqrt(2) * erfinv(2 * U - 1) + Nvar(1); dst = src + noise .* flag; dst = uint8(dst); end
Box-Muller算法代码
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45clc; clear; % 验证高斯噪声--------------- ep = 1e-3; %间隔 x = -4 : ep : 4; num = length(x); U1 = rand(1, num); U2 = rand(1, num); y = sqrt(-2 * log(U1)) .* cos(2*pi*U2); %Box-Muller公式 [f, xi] = ksdensity(y, x); figure(1); plot(x, f); % 添加高斯噪声-------------- img = imread('lena.bmp'); Nvar = [0 50]; % 均值0，标准差50 rate = 0.5; % 50%的区域加噪声 img_processed = add_Gaussian_noise(img, Nvar, rate); % 作图 figure(2); subplot(1, 2, 1); imshow(img); title('src'); subplot(1, 2, 2); imshow(img_processed); title('dst'); function dst = add_Gaussian_noise(src, Nvar, rate) % src --> raw img to be processed % Nvar --> [mean, std] % rate --> the rate of noise [r, c] = size(src); src = double(src); flag = (rand(r,c) > rate); U1 = rand(r, c); U2 = rand(r, c); noise = Nvar(2) * sqrt(-2 * log(U1)) .* cos(2 * pi * U2) + Nvar(1); dst = src + noise .* flag; dst = uint8(dst); end
拒绝采样代码
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54clc; clear; % 检验高斯分布------------ ep = 1e-3; x = -5 : ep : 5; %five sigma top = 4 * 1 / 10; %由于均匀分布U~(-5,5)，则p=0.1；但高斯分布最大值0.4，因此k取4。 sample_num = 1e5; %采样点1e5个 U = rand(1, sample_num) * 10 - 5; gaussian = @(x) 1/sqrt(2*pi) * exp(-x.^2 / 2); sample_id = (rand(1, sample_num) * top) <= gaussian(U); %接受的id sample = U(sample_id); [f, xi] = ksdensity(sample, x); figure(1); plot(x, f); % 添加高斯噪声-------------- img = imread('lena.bmp'); Nvar = [0 50]; rate = 0.5; img_processed = add_Guassian_noise(img, Nvar, rate); % 作图 figure(2); subplot(1, 2, 1); imshow(img); title('src'); subplot(1, 2, 2); imshow(img_processed); title('dst'); function dst = add_Guassian_noise(src, Nvar, rate) % src --> raw img to be processed % Nvar --> [mean, std] % rate --> the rate of noise [r, c] = size(src); src = double(src); flag = (rand(r,c) < rate); sample_num = r * c; %每次取样r*c个，得到接受的个数n noise = []; top = 4 * 1 / 10; while(length(noise) < sample_num) %取样n达到r*c后退出循环 U = 10 * rand(1, sample_num) - 5; gau = 1/sqrt(2*pi) * exp(-U.^2 / 2); sample_id = (rand(1, sample_num) * top <= gau); noise = [noise U(sample_id)]; end noise = noise(1, 1:sample_num); noise = reshape(noise, [r, c]); noise = Nvar(2) * noise + Nvar(1); dst = src + noise .* flag; dst = uint8(dst); end
效果
检验
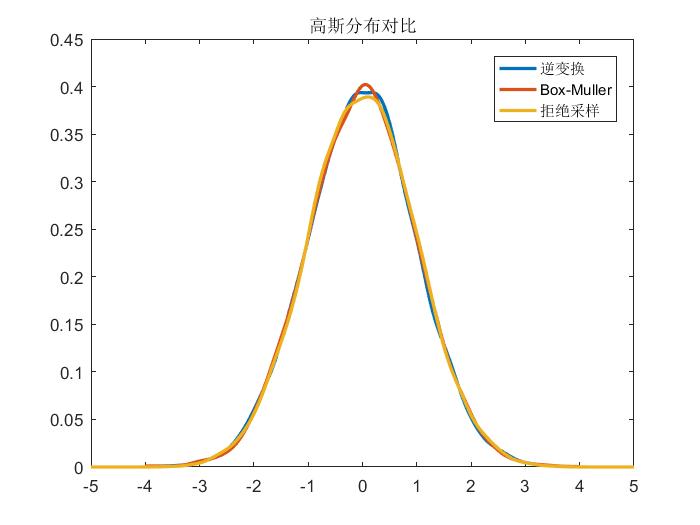
算法效果
引用
- https://blog.csdn.net/renwudao24/article/details/44463489
- https://www.jianshu.com/p/cb916e1ba399
- https://blog.csdn.net/libing_zeng/article/details/81842245?depth_1-utm_source=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-1&utm_source=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-1
最后
以上就是英勇猫咪最近收集整理的关于均匀分布产生高斯分布的全部内容，更多相关均匀分布产生高斯分布内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。
发表评论 取消回复