1. 首页
  2. 文章中心
  3. python

BasicMotions数据集的分析处理简介

62 阅读 0 评论
我是靠谱客的博主 害羞秀发，最近开发中收集的这篇文章主要介绍BasicMotions数据集的分析处理简介，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

简介

数据集描述：The data was generated as part of a student project where four students performed four activities whilst wearing a smart watch. The watch collects 3D accelerometer and a 3D gyroscope It consists of four classes, which are walking, resting, running andbadminton. Participants were required to record motion a total of five times, and the data is sampled once every tenth of a second, for a ten second period.
数据集
本次采取单变量进行分析，使用传感器1的数据进行分析，进而提取四种运动的特征。

FFT(快速傅里叶变换）

对与时序数据集，很难发现其中的规律时就要转为频域上进行分析。从时域转到频域后可以进行一系列操作如滤波等。（近期看论文，有将傅里叶变换后的实部和虚部做为网络的输出可以得到比较好的预测，还没有具体看）

from scipy.io import arff
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
from scipy.fftpack import fft


plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示符号

def FFT(y1,x,name):
    y = y1.tolist()
    yy=fft(y)  #快速傅里叶变换
    yreal=yy.real   #获取实数部分
    yimag=yy.imag   #获取虚数部分

    yf=abs(fft(y))  #取绝对值
    yf1=abs(fft(y))/len(x)  #归一化处理
    yf2=yf1[range(int(len(x)/2))] #由于对称性，只取一半区间

    xf=np.arange(len(y))   #频率
    xf1=xf
    xf2=xf[range(int(len(x)/2))]  #取一半区间

    #逆快速傅里叶
    ifft=np.fft.ifft(yy)

    plt.subplot(221)
    plt.plot(x, y)
    plt.title(name+':Original wave',fontsize=7)

    plt.subplot(222)
    plt.plot(xf, yf, 'r')
    plt.title('FFT of Mixed wave(two sides frequency range)', fontsize=7, color='#7A378B')  # 注意这里的颜色可以查询颜色代码表

    # plt.subplot(223)
    # plt.plot(x,ifft, 'g')
    # plt.title('FFT of Mixed wave(normalization)', fontsize=7, color='r')

    plt.subplot(223)
    plt.plot(xf2, yf2, 'b')
    plt.title('FFT of Mixed wave)', fontsize=7, color='#F08080')

    plt.subplot(224)
    plt.plot(x, ifft, 'g')
    plt.title('ifft', fontsize=7, color='r')

    plt.show()


data = arff.loadarff(r'D:BasicMotionsBasicMotionsDimension1_TEST.arff')
df = pd.DataFrame(data[0]).set_index('activity')
print(df)
# print(df.shape[0])
y1 = df.iloc[0:10]
y2=df.iloc[10:20]
y3=df.iloc[20:30]
y4=df.iloc[30:40]
y_1=pd.concat([y1.iloc[0],y1.iloc[1]])
y_2=pd.concat([y2.iloc[0],y2.iloc[1]])
y_3=pd.concat([y3.iloc[0],y3.iloc[1]])
y_4=pd.concat([y4.iloc[0],y4.iloc[1]])
for i in range(8):
    #Standing
    yy1=pd.concat([y_1,y1.iloc[i+1]],axis=0,ignore_index=False)
    y_1 = yy1
    #Running
    yy2 = pd.concat([y_2, y2.iloc[i + 1]], axis=0, ignore_index=False)
    y_2 = yy2
    # Walking
    yy3 = pd.concat([y_3, y3.iloc[i + 1]], axis=0, ignore_index=False)
    y_3 = yy3
    # Badminton
    yy4 = pd.concat([y_4, y4.iloc[i + 1]], axis=0, ignore_index=False)
    y_4 = yy4

x=np.linspace(0,10,1000)
name1='Standing'
name2='Running'
name3='Walking'
name4='Badminton'
FFT(y_1,x,name1)
#FFT(y_2,x,name2)
#FFT(y_3,x,name3)
#FFT(y_4,x,name4)

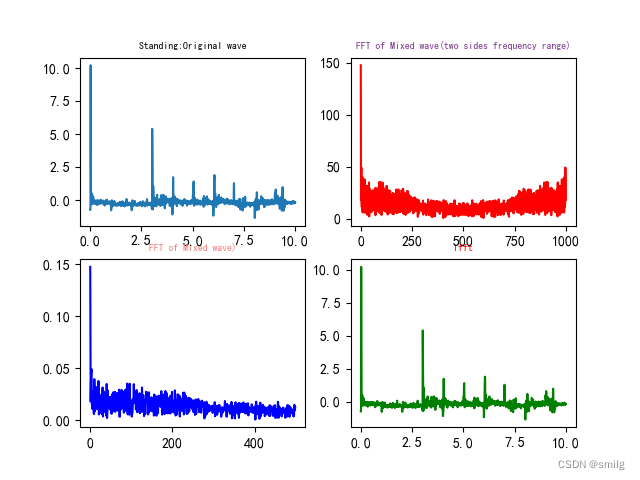
因为每个运动都有10个人的数据，将10个人的数据进行了一个拼接。
得到的结果如下图

在这里插入图片描述

小波变换

from scipy.io import arff
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
import  pywt


plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示符号

def Pywt(y1,x,name,wavename1,totalscal1):
    y = y1.tolist()
    wavename=wavename1
    totalscal=totalscal1
    fc=pywt.central_frequency(wavename)
    cparam=2*fc*totalscal
    scales=cparam/np.arange(totalscal,1,-1)
    [cwtmatr,frequencies]=pywt.cwt(y,scales,wavename,1.0/10)
    plt.contourf(x,frequencies,abs(cwtmatr))
    plt.subplots_adjust(hspace=0.4)
    plt.tight_layout
    plt.xlabel('时间/s')
    plt.title(name)
    plt.show()



data = arff.loadarff(r'D:BasicMotionsBasicMotionsDimension1_TEST.arff')
df = pd.DataFrame(data[0]).set_index('activity')
print(df)
print(df.shape)
y1 = df.iloc[0:10]
y2=df.iloc[10:20]
y3=df.iloc[20:30]
y4=df.iloc[30:40]
y_1=pd.concat([y1.iloc[0],y1.iloc[1]])
y_2=pd.concat([y2.iloc[0],y2.iloc[1]])
y_3=pd.concat([y3.iloc[0],y3.iloc[1]])
y_4=pd.concat([y4.iloc[0],y4.iloc[1]])
for i in range(8):
    #Standing
    yy1=pd.concat([y_1,y1.iloc[i+1]],axis=0,ignore_index=False)
    y_1 = yy1
    #Running
    yy2 = pd.concat([y_2, y2.iloc[i + 1]], axis=0, ignore_index=False)
    y_2 = yy2
    # Walking
    yy3 = pd.concat([y_3, y3.iloc[i + 1]], axis=0, ignore_index=False)
    y_3 = yy3
    # Badminton
    yy4 = pd.concat([y_4, y4.iloc[i + 1]], axis=0, ignore_index=False)
    y_4 = yy4
name1='Standing'
name2='Running'
name3='Walking'
name4='Badminton'
x=np.arange(0,10,0.01)
wavename='cgau8'
totalscal=256
Pywt(y_1,x,name1,wavename,totalscal)
Pywt(y_2,x,name2,wavename,totalscal)
Pywt(y_3,x,name3,wavename,totalscal)
Pywt(y_4,x,name4,wavename,totalscal)

结果如下图、

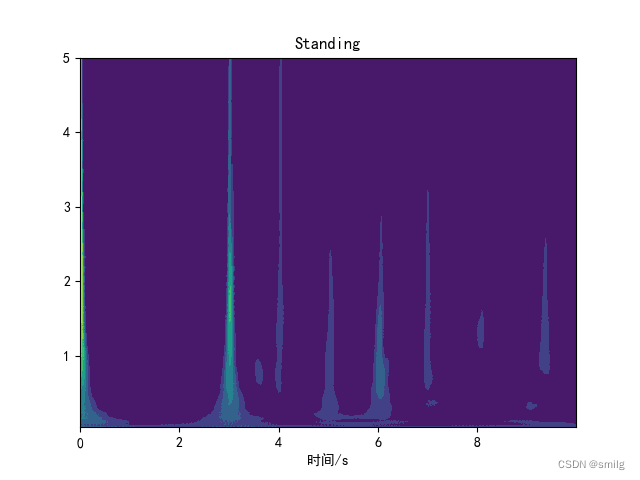
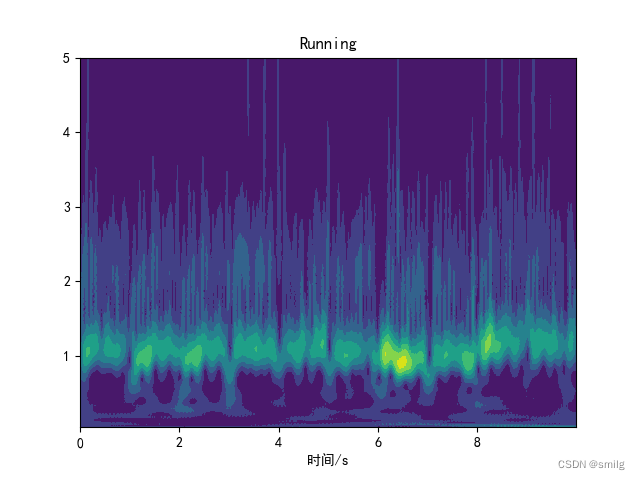
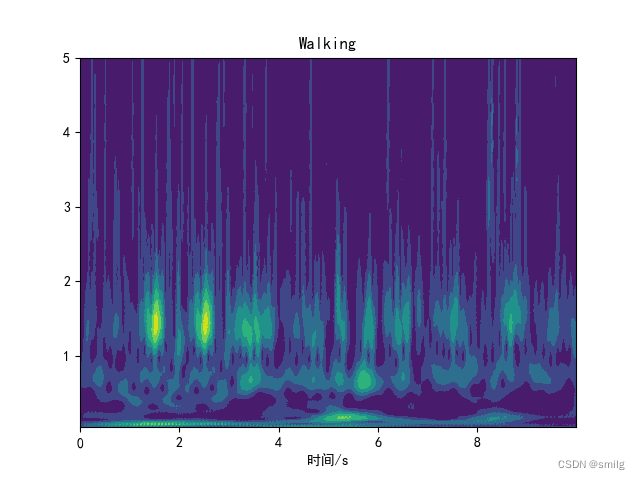
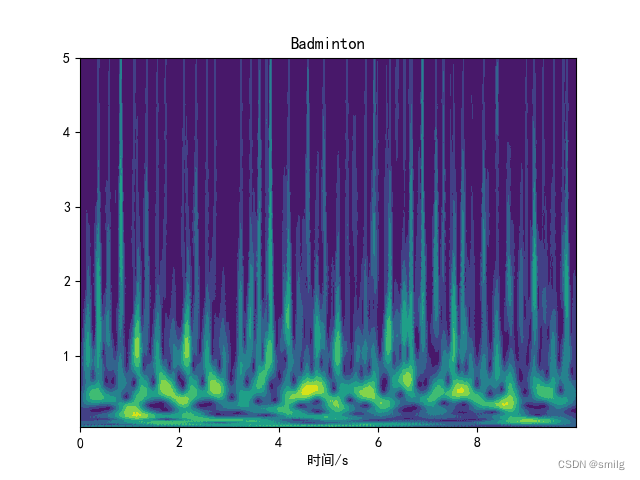
在这里插入图片描述在这里插入图片描述在这里插入图片描述在这里插入图片描述
从小波时频图种可以看出四种运动的特征还是有很大区别。进而使用神经网络训练进而分类。

小波包分解

通过小波包分解，把不同频段以能量的形式展示。

from scipy.io import arff
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
import  pywt


plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示符号


def wpd_plt(signal, n):
    x = np.arange(0, 1000, 1)
    # wpd分解
    wp = pywt.WaveletPacket(data=signal, wavelet='db1', mode='symmetric', maxlevel=n)

    # 计算每一个节点的系数，存在map中
    map = {}
    map[1] = signal
    #print(map[1])
    for row in range(1, n + 1):
        lev = []
        for i in [node.path for node in wp.get_level(row, 'freq')]:
            map[i] = wp[i].data

    # 作图
    plt.figure(figsize=(15, 10))
    plt.subplot(n + 1, 1, 1)  # 绘制第一个图
    plt.plot(x,map[1])
    for i in range(2, n + 2):
        level_num = pow(2, i - 1)  # 从第二行图开始，计算上一行图的2的幂次方
        # 获取每一层分解的node
        re = [node.path for node in wp.get_level(i - 1, 'freq')]
        for j in range(1, level_num + 1):
            plt.subplot(n + 1, level_num, level_num * (i - 1) + j)
            plt.plot(map[re[j - 1]])  # 列表从0开始
    plt.show()
    #绘制小波包能量图
    wp=pywt.WaveletPacket(data=signal,wavelet='db1',mode='symmetric',maxlevel=n)
    re=[]
    for i in [node.path for node in wp.get_level(n,'freq')]:
        re.append(wp[i].data)
    #第n层能量特征
    enery=[]
    for i in re:
        enery.append(pow(np.linalg.norm(i,ord=None),2))
    j=0
    for i in enery:
        j=j+1
        print(i)
    plt.figure(dpi=80)
    # 柱子总数
    N = j
    values = enery
    # 包含每个柱子下标的序列
    index = np.arange(N)
    # 柱子的宽度
    width = 0.45
    # 绘制柱状图, 每根柱子的颜色为紫罗兰色
    p2 = plt.bar(index, values, width, label="num", color="#87CEFA")
    plt.xlabel('clusters')
    plt.ylabel('Wavel energy')
    plt.title('Cluster Distribution')
    # 添加纵横轴的刻度
    plt.xticks(index, ('7', '8', '9', '10', '11', '12', '13', '14'))
    # plt.yticks(np.arange(0, 10000, 10))
    plt.legend(loc="upper right")
    plt.show()


data = arff.loadarff(r'D:BasicMotionsBasicMotionsDimension1_TEST.arff')
df = pd.DataFrame(data[0]).set_index('activity')

y1 = df.iloc[0:10]
y2=df.iloc[10:20]
y3=df.iloc[20:30]
y4=df.iloc[30:40]
y_1=pd.concat([y1.iloc[0],y1.iloc[1]])
y_2=pd.concat([y2.iloc[0],y2.iloc[1]])
y_3=pd.concat([y3.iloc[0],y3.iloc[1]])
y_4=pd.concat([y4.iloc[0],y4.iloc[1]])
for i in range(8):
    #Standing
    yy1=pd.concat([y_1,y1.iloc[i+1]],axis=0,ignore_index=False)
    y_1 = yy1
    #Running
    yy2 = pd.concat([y_2, y2.iloc[i + 1]], axis=0, ignore_index=False)
    y_2 = yy2
    # Walking
    yy3 = pd.concat([y_3, y3.iloc[i + 1]], axis=0, ignore_index=False)
    y_3 = yy3
    # Badminton
    yy4 = pd.concat([y_4, y4.iloc[i + 1]], axis=0, ignore_index=False)
    y_4 = yy4
wpd_plt(y_1,3)
wpd_plt(y_2,3)
wpd_plt(y_3,3)
wpd_plt(y_4,3)


# 原始频率为1000Hz，分成8份，每份为125Hz，因此
# 7是指0-125Hz频段
# 8是指125-250Hz频段
# ...
# 13是指750-875Hz频段
# 14是指875-1000Hz频段

结果如图，3次分解后，统计能量直方图，可以发现4种运动还是有很大的不同。这里我只放了一种运动的。
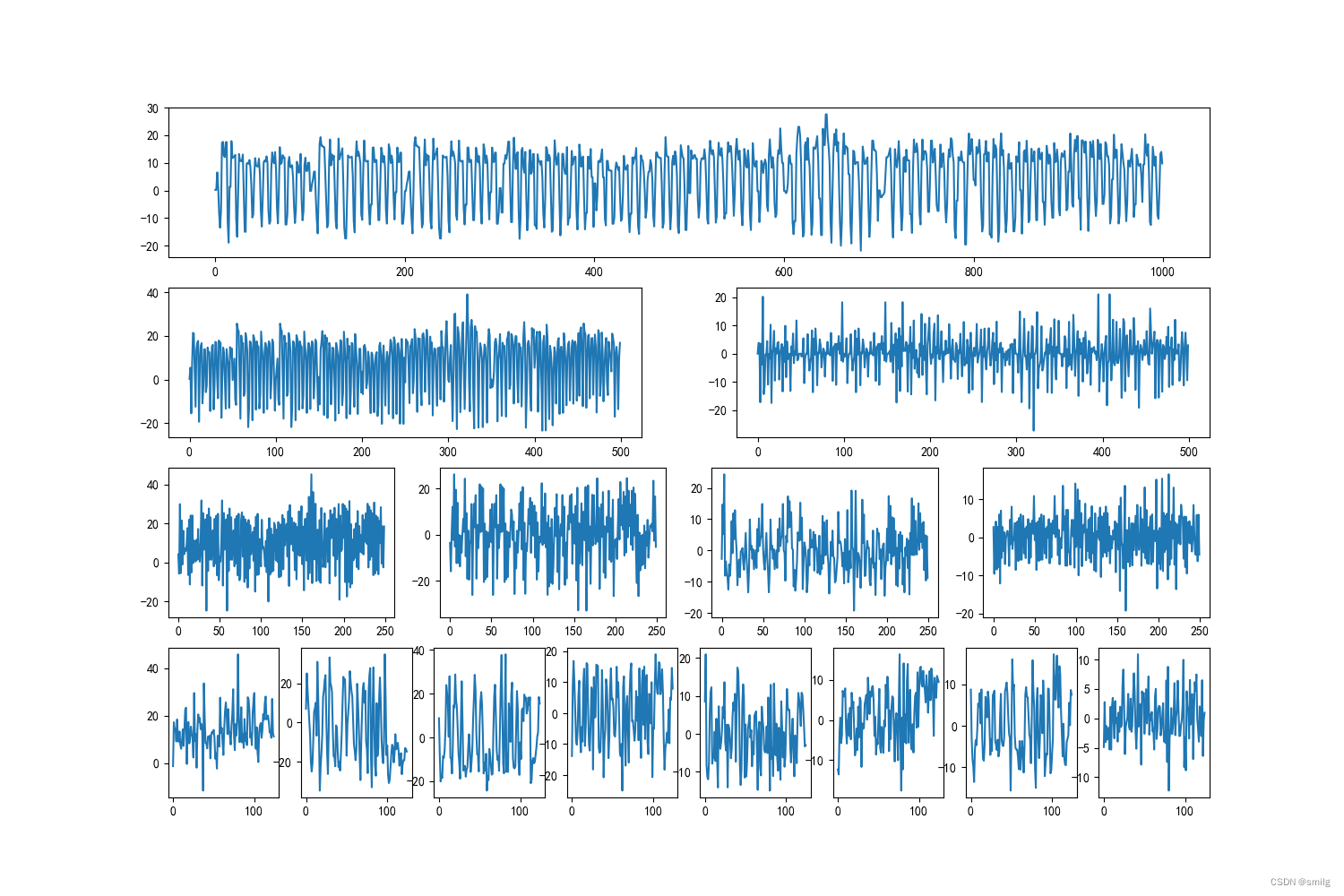
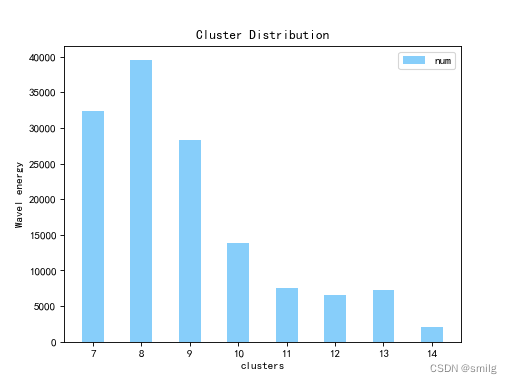
在这里插入图片描述在这里插入图片描述
关于FFT、小波、小波包有很多大佬写的很好。本文只在BasicMotions数据集进行实操。

最后

以上就是害羞秀发为你收集整理的BasicMotions数据集的分析处理简介的全部内容，希望文章能够帮你解决BasicMotions数据集的分析处理简介所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。

本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。
点赞(41)

相关文章

python多元线性回归模型案例_Python 实战多元线性回归模型，附带原理+代码
python多元线性回归模型案例_Python 实战多元线性回归模型，附带原理+代码
python数据分析多元 线性回归1 基本环境设置2 读取数据加载3 y预估方法与误差方法设计4 梯度下降设计5 数据处理6 模型运行7 模型可视化8 误差绘图
python数据分析多元 线性回归1 基本环境设置2 读取数据加载3 y预估方法与误差方法设计4 梯度下降设计5 数据处理6 模型运行7 模型可视化8 误差绘图
读书系列之LSTM和GRU背后的数学公式
读书系列之LSTM和GRU背后的数学公式
LSTM 详细公式与图解
LSTM 详细公式与图解
BasicMotions数据集的分析处理简介
BasicMotions数据集的分析处理简介
RNN_LSTM公式
RNN_LSTM公式
标准的LSTM网络以及公式
标准的LSTM网络以及公式
LSTM算法公式
LSTM算法公式

评论列表共有 0 条评论

立即
投稿
返回
顶部