一、什么是序列模型
面对图像数据,研究人员设计了专门的神经网络结构来利用数据的规律。 换句话说,如果我们拥有一张图像,图像中的内容看起来就像模拟电视时代的测试图,那么对图像中的像素位置进行重排,就会对图像中的内容推理造成极大的困难,因为各个像素间都是独立的。
最重要的是,到目前为止我们默认数据都来自于某种分布,并且所有样本都是独立同分布的(independently and identically distributed, i.i.d.)。 然而,大多数的数据并非如此。 例如,文章中的单词是按顺序写的,如果顺序被随机地重排,就很难理解文章原始的意思。 同样,视频中的图像帧、对话中的音频信号以及网站上的浏览行为都是有顺序的。 因此,针对此类数据而设计特定模型,可能效果会更好。
循环神经网络通过引入状态变量存储过去的信息和当前的输入,从而可以确定当前的输出。
简言之,卷积神经网络可以有效地处理空间信息,循环神经网络(recurrent neural network, RNN)这种设计可以更好地处理序列信息。
想象一下你正在看网飞(Netflix,一个国外的视频网站)上的电影。作为一个很棒的网飞用户,你决定对每一部电影都给出评价。毕竟,一部好的电影值得好电影这个名声,而且你想看更多的好电影,对吧?事实证明,事情并不那么简单。随着时间的推移,人们对电影的看法会发生很大的变化。事实上,心理学家甚至对某些效应起了名字:
- 锚定(anchoring),基于其他人的意见。例如,奥斯卡颁奖后,受到关注的电影的评分会上升,尽管它还是原来那部电影。这种影响将持续几个月,直到人们忘记了这部电影曾经获得的奖项。结果表明,这种效应会使评分提高半个百分点以上。
- 享乐适应(hedonic adaption),即人类迅速接受并且适应一种更好或者更坏的情况作为新的常态。例如,在看了很多好电影之后,人们会强烈期望下部电影会一样好或者更好。因此,在许多精彩的电影被看过之后,即使是一部普通的也可能被认为是糟糕的。
- 季节性(seasonality),少有观众喜欢在八月看圣诞老人的电影。
- 有时候,电影会由于导演或演员在制作中的不当行为变得不受欢迎。
简而言之,电影评分决不是固定不变的。因此,使用时间动力学可以得到更准确的电影推荐 [Koren, 2009] 。当然,序列数据不仅仅是关于电影评分的。下面给出了更多的场景。
- 在使用应用程序时,许多用户都有很强的特定习惯。例如,在学生放学后社交媒体应用更受欢迎。在市场开放时股市交易软件更常用。
- 预测明天的股价要比填补昨天遗失的股价的更困难,尽管两者都只是估计一个数字。毕竟,先见之明比事后诸葛亮难得多。在统计学中,前者(对超出已知观测范围进行预测)称为
外推法(extrapolation),而后者(在现有观测值之间进行估计)称为 内插法(interpolation)。 - 在本质上,音乐、语音、文本和视频都是连续的。如果它们的序列被我们重排,那么原有的意义就会失去。文本标题 狗咬人 远没有 人咬狗那么令人惊讶,尽管组成两句话的字完全相同。
- 地震具有很强的相关性,即大地震发生后,很可能会有几次较小的余震,这些余震的强度比不是大地震的余震要大得多。事实上,地震是时空相关的,即余震通常发生在很短的时间跨度和很近的距离内。
- 人类之间的互动也是连续的,这可以从推特上的争吵和辩论中看出。
统计工具
对于一个时许序列,在时间
t
t
t观察到
x
t
x_{t}
xt,那么得到
T
T
T个不独立的随机变量
(
x
1
,
…
x
T
)
∼
p
(
x
)
left(x_{1}, ldots x_{T}right) sim p(mathbf{x})
(x1,…xT)∼p(x)
我们对这个联合概率,使用条件概率展开
p
(
a
,
b
)
=
p
(
a
)
p
(
b
∣
a
)
=
p
(
b
)
p
(
a
∣
b
)
p(a, b)=p(a) p(b mid a)=p(b) p(a mid b)
p(a,b)=p(a)p(b∣a)=p(b)p(a∣b)
那么我们对一个序列用上述公式展开,如下图所示:

先算
p
(
x
1
)
pleft(x_{1}right)
p(x1)的概率,十分好算
再算
p
(
x
2
)
pleft(x_{2}right)
p(x2)的概率,即在
x
1
x_{1}
x1发生的情况下求解,
x
2
x_{2}
x2是依赖于
x
1
x_{1}
x1的
我们也可以进行反序计算,先求
x
T
x_{T}
xT的概率,然后推前面的事情,但是这种情况一般在物理意义上是行不通的,比如一个真实的事件,你无法根据未来的事件推前面的事件,很有可能未来事件时基于前面的事件产生的

条件概率建模
我们核心的事情就是对
p
(
x
t
∣
x
1
,
…
x
t
−
1
)
=
p
(
x
t
∣
f
(
x
1
,
…
x
t
−
1
)
)
pleft(x_{t} mid x_{1}, ldots x_{t-1}right)=pleft(x_{t} mid fleft(x_{1}, ldots x_{t-1}right)right)
p(xt∣x1,…xt−1)=p(xt∣f(x1,…xt−1))
进行建模,我们的做法是对前
t
−
1
t-1
t−1个进行建模,表示为一个模型(函数),这种对见过的数据建模,也叫自回归模型,那么接下来的事情就是如何对
f
f
f进行建模,主流方案有两种:
- 马尔科夫假设
- 潜变量模型
本文只对潜变量模型进行介绍,有时间再进行后续补充。
一个序列模型的例子:
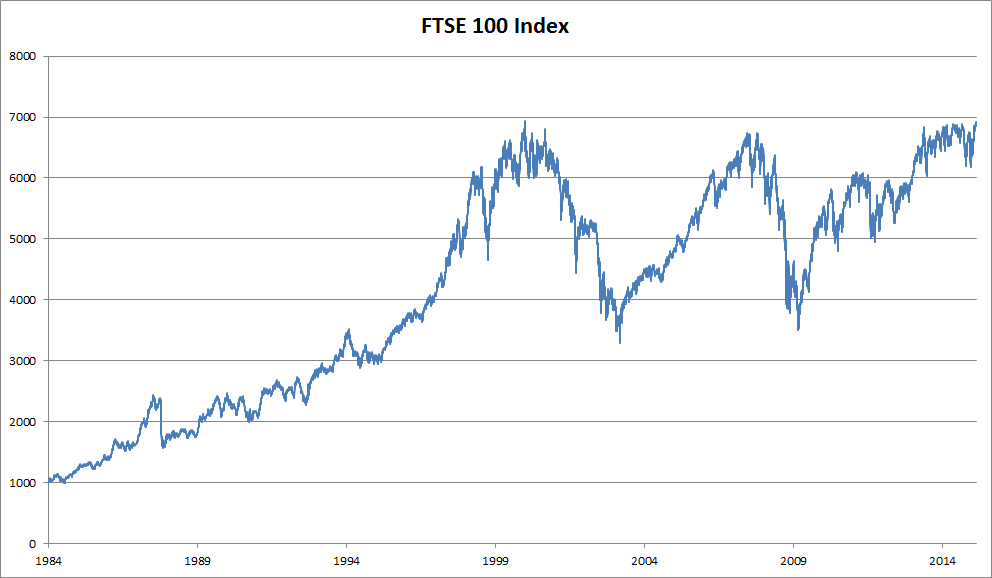
我们以近30年的富时100指数为例,其中,用
x
t
x_{t}
xt表示价格,即在 时间步(time step)
t
∈
Z
+
t in mathbb{Z}^{+}
t∈Z+ 时,观察到的价格
x
t
x_{t}
xt 。请注意,
t
t
t对于本文中的序列通常是离散的,并随整数或其子集而变化。假设一个交易员想在
t
t
t日的股市中表现良好,于是通过以下途径预测
x
t
x_{t}
xt:
x
t
∼
P
(
x
t
∣
x
t
−
1
,
…
,
x
1
)
x_{t} sim Pleft(x_{t} mid x_{t-1}, ldots, x_{1}right)
xt∼P(xt∣xt−1,…,x1)
二、潜变量模型
我们引入一个潜变量
h
t
h_{t}
ht去总结过去信息,
h
t
=
f
(
x
1
,
…
x
t
−
1
)
h_{t}=fleft(x_{1}, ldots x_{t-1}right)
ht=f(x1,…xt−1)
那么对于公式
p
(
x
t
∣
f
(
x
1
,
…
x
t
−
1
)
)
pleft(x_{t} mid fleft(x_{1}, ldots x_{t-1}right)right)
p(xt∣f(x1,…xt−1))来说,就变成了
x
t
=
p
(
x
t
∣
h
t
)
x_{t}=pleft(x_{t} mid h_{t}right)
xt=p(xt∣ht)
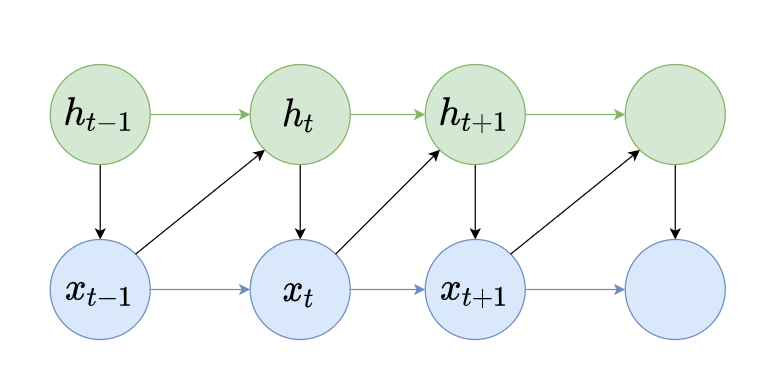
对于
x
x
x的下一个序列
x
t
x_{t}
xt来说,我们通过
x
x
x计算
x
t
x_{t}
xt,
x
t
x_{t}
xt既和
x
x
x相关,又和
h
t
h_{t}
ht相关
同时
h
t
h_{t}
ht是通过上一个时刻的
x
x
x和潜变量
h
h
h得到的,我们潜变量就可以做到时刻更新,影响此时刻的输出,并结合输出生成下一时刻的潜变量
这样我们就可以拆分出来两个简单模型,
p
(
h
t
∣
h
t
−
1
,
x
t
−
1
)
pleft(h_{t} mid h_{t-1}, x_{t-1}right)
p(ht∣ht−1,xt−1)
p
(
x
t
∣
h
t
,
x
t
−
1
)
pleft(x_{t} mid h_{t}, x_{t-1}right)
p(xt∣ht,xt−1)
这两个都是简单模型,利用多层感知机算法是不是就可以进行建模
三、RNN模型
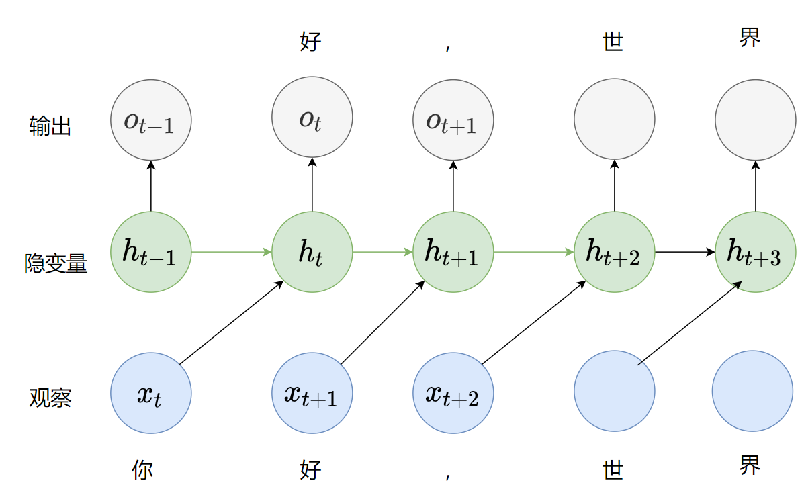
仔细观察此图并与隐变量模型做对比,发现当前时刻
h
t
h_{t}
ht决定了当前输出
o
t
o_{t}
ot,而
h
t
h_{t}
ht不能用
x
t
x_{t}
xt的东西,而是
x
t
−
1
x_{t-1}
xt−1,那么这样做对语言模型有什么用呢?
假设我们的输入是“你”,那么我回去更新我的隐变量,并去预测“好”字,接下来我观测到了“好”,我再去更新隐变量,输出“,”。其实
o
t
o_{t}
ot是用来match到你的输入
x
t
x_{t}
xt,但你在生成
o
t
o_{t}
ot时你看不到
x
t
x_{t}
xt,你的当前时刻的输出是要预测当前时刻的输入。
那么计算损失的时候我们计算
o
t
o_{t}
ot与
x
t
x_{t}
xt的损失就可以了。
更新当前状态:
h
t
=
ϕ
(
W
h
h
h
t
−
1
+
W
h
x
x
t
+
b
h
)
mathbf{h}_{t}=phileft(mathbf{W}_{h h} mathbf{h}_{t-1}+mathbf{W}_{h x} mathbf{x}_{t}+mathbf{b}_{h}right.)
ht=ϕ(Whhht−1+Whxxt+bh)
输出:
o
t
=
ϕ
(
W
h
o
h
t
+
b
o
)
mathbf{o}_{t}=phileft(mathbf{W}_{h o} mathbf{h}_{t}+mathbf{b}_{o}right)
ot=ϕ(Whoht+bo)
先看第一个公式,
W
h
x
mathbf{W}_{h x}
Whx代表了
x
t
−
1
x_{t-1}
xt−1到
h
t
h_{t}
ht之间的权重,如果只看这一部分是一个做了线性变换的多层感知机。而
W
h
h
mathbf{W}_{h h}
Whh表示
h
t
−
1
h_{t-1}
ht−1到
h
t
h_{t}
ht之间的权重,再加上偏质
b
h
b_{h}
bh,两者共同主导了
h
t
h_{t}
ht的状态更新。
第二个公式,
W
h
o
{W}_{h o}
Who代表
h
t
到
h_{t}到
ht到o_{t}的权重。
具体实例
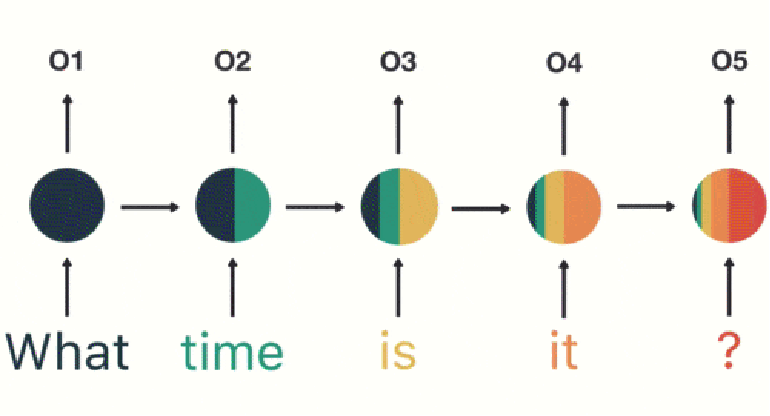
假如需要判断用户的说话意图(问天气、问时间、设置闹钟…),用户说了一句“what time is it?”我们需要先对这句话进行分词:

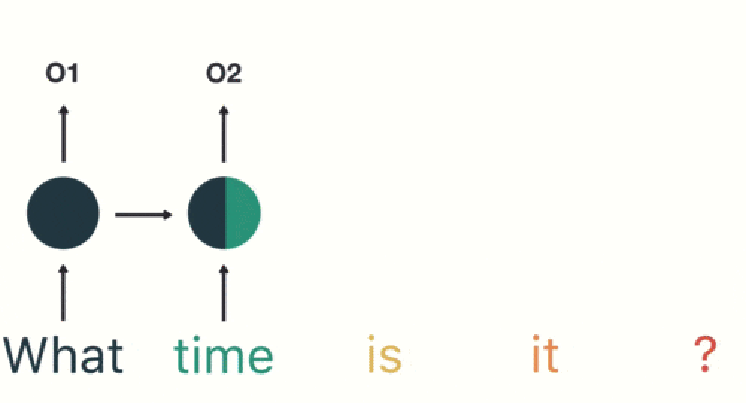
然后按照顺序输入 RNN ,我们先将“what”作为 RNN 的输入,得到输出「01」

然后,我们按照顺序,将“time”输入到 RNN 网络,得到输出「02」。
这个过程我们可以看到,输入 “time” 的时候,前面 “what” 的输出也产生了影响(隐藏层中有一半是黑色的)。

以此类推,前面所有的输入都对未来的输出产生了影响,我们可以看到圆形隐藏层中包含了前面所有的颜色。如下图所示:
当我们判断意图的时候,只需要最后一层的输出「05」,如下图所示:
缺点
通过上面的例子,我们已经发现,短期的记忆影响较大(如橙色区域),但是长期的记忆影响就很小(如黑色和绿色区域),这就是 RNN 存在的短期记忆问题。
最后
以上就是含蓄哑铃最近收集整理的关于RNN循环神经网络——从问题提出到原理解释一、什么是序列模型二、潜变量模型的全部内容,更多相关RNN循环神经网络——从问题提出到原理解释一、什么是序列模型二、潜变量模型内容请搜索靠谱客的其他文章。








发表评论 取消回复