文章目录
- 循环神经网络(RNN)
- RNN网络结构
- RNN的神经元个数
- RNN前向传播
- RNN反向传播
- RNN的梯度消失问题
- 长短期记忆网络(LSTM)
- LSTM结构
- LSTM反向传播
- LSTM神经元个数
循环神经网络(RNN)
如果我们的数据是一个时间序列,且序列长短不一,在每一个时间点存在数据,如下 < … , x t − 2 , x t − 1 , x t , x t + 1 , x t + 2 , ⋯ > <dots , x_{t-2}, x_{t-1}, x_{t}, x_{t+1},x_{t+2}, dots> <…,xt−2,xt−1,xt,xt+1,xt+2,⋯>可以说不同时刻的数据相互之间十分可能存在某种联系。
对于这种数据,如果考虑使用DNN或者CNN,首先,DNN与CNN的batch维度是不起作用的,因为batch中的数据在前向传播是独立进行,反向传播仅仅把误差相加,DNN与CNN显然无法很好的学习batch中的数据在时间上的相关规律。另一方面,如果我们明确知道这种数据的时间连续性在前100个时间点内,我们可以增加DNN的输入神经元或CNN的输入通道数到100,把前100个时间点的数据当做特征字段 x x x输入,来得到该时间点的目标输出 y y y。但是实际应用中,序列长短不一(可能还不够100),也有可能与超过100个时间点之前的数据相关系,这样我们的CNN和DNN就不好解决了,因此引入了RNN。
RNN网络结构
RNN的一个cell往往占据一个隐层,只有一个隐层的RNN其网络结构如下图左,按时间轴展开后就得到了右边的图像。
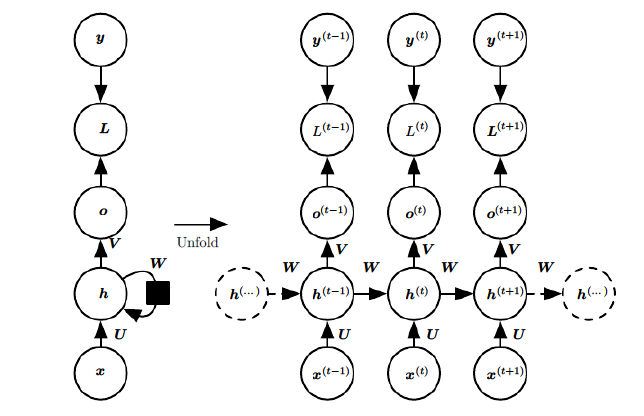
其中的 h h h所代表的模块即是RNN的cell,它有一个箭头(权重是 W W W)指向自己,这就是"循环"二字的由来。一般看RNN要看其展开后的图像, x x x是网络的输入, h h h( h i d d e n hidden hidden的缩写)是隐藏层状态, o o o是网络的输出, y y y是期望输出, L L L就是 y y y与 o o o的损失,右上角的 t t t即是在 t t t时刻的数据,我们看 t t t时刻的隐藏层状态 h ( t ) h^{(t)} h(t),它是由 t t t时刻的输入 x ( t ) x^{(t)} x(t)和 t − 1 t-1 t−1时刻的隐藏层状态 h ( t − 1 ) h^{(t-1)} h(t−1)共同决定,可见RNN存在同一隐层内部的传播,这在CNN和DNN这种前馈神经网络结构中是不存在的,正是由于这种隐层内的传播,让RNN能够综合学习之前时刻的数据,来输出当前时刻的数据。
上图中的权重 U , V , W U,V,W U,V,W,对于展开后的RNN,是参数共享的,不同时刻的 x 、 h 、 o x、h、o x、h、o在计算时,共享相同的权重值。
在不同的时刻,RNN有不同的输入 x ( t ) x^{(t)} x(t),同样就也有对应的输出 y ( t ) y^{(t)} y(t),但有时我们可能在输入完一个序列 x ( 1 ) … x ( n ) x^{(1)}dots x^{(n)} x(1)…x(n)后,只要最后的输出 y ( n ) y^{(n)} y(n),或者只要部分时刻的输出,或者有其它更复杂的情况,根据输入输出,我们可以对RNN进行分类。
当然RNN一般都不会只有一个隐层,我们可以通过叠加RNN cell来增加RNN的深度,构成深度RNN结构,一般RNN的深度越深,学习能力越强,但是学习速率会下降。下面给出一个有5个隐层的RNN结构。
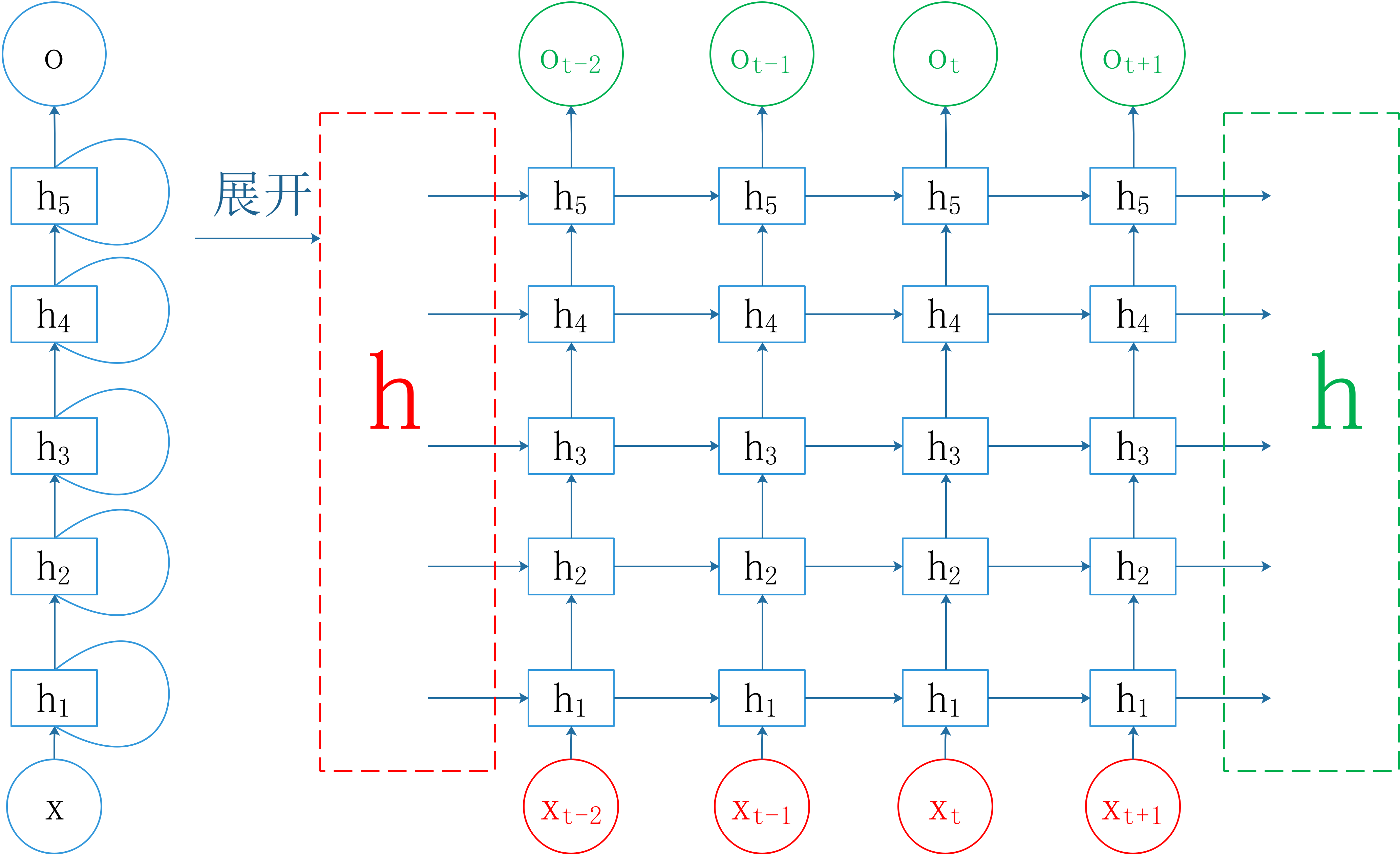
红色部分表示RNN的输入部分,绿色部分表示RNN的输出部分。不难看出来,RNN的输入包含两个部分,除了数据输入 x x x外,我们还要初始化隐藏层状态的输入 h h h,同理,RNN的输出也包含两个部分。
RNN的神经元个数
我们在比较不同的神经网络对某一具体问题的效果时,需要把隐层的神经元个数设置成一样的。我一直认为RNN是没有神经元这个概念的,只有RNN cell这个概念,但是一个前辈明确指出RNN是有神经元的概念。针对RNN的神经元个数,网上有不同的说法,blog认为RNN的神经元个数近似可以看成,待更新参数(权值和偏置)的个数,还有人认为RNN某一隐层的神经元个数就是把RNN展开后,RNN结构在时间上的迭代次数,即输入的时间序列的长度。这两种定义都不是很到位,这样定义神经元,无法很好地对接DNN中的神经元。
在说RNN的神经元之前,先说明一下RNN的输入 x x x的size。
RNN的输入 x x x的size可以表示成 ( b a t c h s i z e , s e q u e n c e l e n g t h , i n p u t s i z e ) (batch~size, sequence~length, input~size) (batch size,sequence length,input size),如果我们的batch size是10,对于batch中的一条记录,其包含的时间步总长sequence length是20,即我们的时间序列长是20,batch中的一条记录在某一时刻的特征总数是30,那么我们输入的size是 ( 10 , 20 , 30 ) (10, 20, 30) (10,20,30),同样的,每一个隐藏层的隐藏状态 h h h可以定义成 ( b a t c h s i z e , s e q u e n c e l e n g t h , h i d d e n s i z e ) (batch~size, sequence~length, hidden~size) (batch size,sequence length,hidden size),
我们把只有一个隐层的RNN,其 t − 1 t-1 t−1时刻到 t t t时刻展开的更加彻底,见下图:
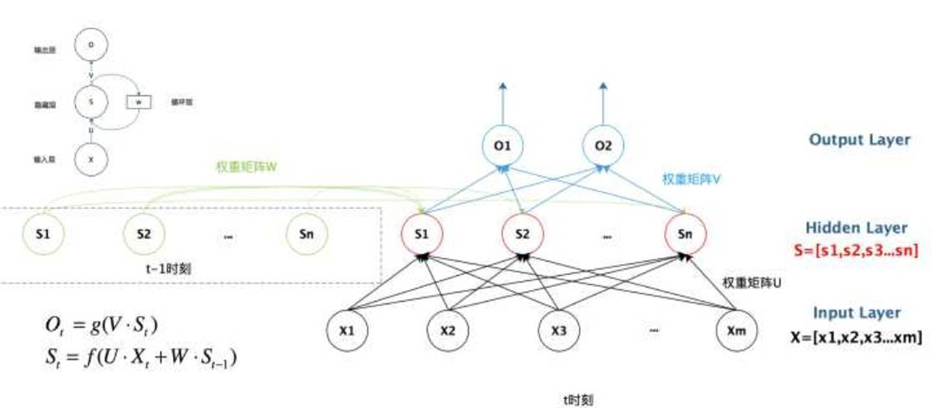
m就是 x x x的size中的 i n p u t s i z e input~size input size,n就是 h h h的size中的 h i d d e n s i z e hidden~size hidden size,这样我们就可以按照看DNN结构的方式,来看RNN的 t t t时刻的结构,可见隐层的神经元个数就是 h i d d e n s i z e hidden~size hidden size。
RNN前向传播
在 t t t时刻,RNN根据该时刻的输入 x t x_{t} xt,和上一时刻保留的信息 h t − 1 h_{t-1} ht−1,按照下面的公式计算该时刻的输出 o t o_{t} ot。 h t = f ( U x t + W h t − 1 + b ) o t = f ( V h t + c ) h_{t} = f(Ux_{t}+Wh_{t-1}+b) \ o_{t} = f(Vh_{t}+c) \ ht=f(Uxt+Wht−1+b)ot=f(Vht+c)
其中 f ( ⋅ ) f(·) f(⋅)是激活函数,最终的损失函数是对需要考虑的所有时刻的损失的叠加 L = ∑ t = 1 T l t = ∑ t = 1 T l ( o t , y t ) L= sumlimits_{t=1}^{T}l_{t}=sumlimits_{t=1}^{T}l(o_{t}, y_{t}) L=t=1∑Tlt=t=1∑Tl(ot,yt)
其中, y t y_{t} yt是 t t t时刻的期望输出。
RNN反向传播
RNN的反向传播基本思路和DNN和CNN的反向传播类似,但是,由于RNN具有时间因素,最后的损失函数又考虑了所有时刻的误差,所以RNN的反向传播要沿着不同时刻的网络结构进行,所以叫做BPTT(Back-Propagation Through Time)。RNN的反向传播要更新的参数包括权重 U , V , W U,V,W U,V,W和偏置 b , c b,c b,c。
以一个隐层的RNN为例,下面的推导针对batch中的一个数据,多个数据只需要求和取平均即可。
损失对
V
V
V和
c
c
c的偏导数如下:
∂
L
∂
V
=
∑
t
=
1
T
∂
l
t
∂
o
t
∂
o
t
∂
V
frac{partial L}{partial V} = sumlimits_{t=1}^{T}frac{partial l_{t}}{partial o_{t}}frac{partial o_{t}}{partial V}
∂V∂L=t=1∑T∂ot∂lt∂V∂ot
∂
L
∂
c
=
∑
t
=
1
T
∂
l
t
∂
o
t
∂
o
t
∂
c
frac{partial L}{partial c} = sumlimits_{t=1}^{T}frac{partial l_{t}}{partial o_{t}}frac{partial o_{t}}{partial c}
∂c∂L=t=1∑T∂ot∂lt∂c∂ot
我们定义RNN中的残差结构如下: δ t = ∂ L ∂ h t = ∑ t = 1 T ∂ l t ∂ h t delta_{t}=frac{partial L}{partial h_{t}} =sumlimits_{t=1}^{T}frac{partial l_{t}}{partial h_{t}} δt=∂ht∂L=t=1∑T∂ht∂lt由于 h t h_{t} ht只传播给 o t o_{t} ot以及 h t + 1 h_{t+1} ht+1(最后的时刻没有 h t + 1 h_{t+1} ht+1),所以 δ t = ∂ L ∂ h t = ∑ t = 1 T ( ∂ l t ∂ o t ∂ o t ∂ h t + ∂ l t ∂ h t + 1 ∂ h t + 1 ∂ h t ) = ∂ l t ∂ o t ∂ o t ∂ h t + ∑ t = 1 T ∂ l t ∂ h t + 1 ∂ h t + 1 ∂ h t = ∂ l t ∂ o t ∂ o t ∂ h t + δ t + 1 ∂ h t + 1 ∂ h t begin{aligned} delta_{t} & =frac{partial L}{partial h_{t}} \ & = sumlimits_{t=1}^{T}(frac{partial l_{t}}{partial o_{t}}frac{partial o_{t}}{partial h_{t}}+frac{partial l_{t}}{partial h_{t+1}}frac{partial h_{t+1}}{partial h_{t}})\ & = frac{partial l_{t}}{partial o_{t}}frac{partial o_{t}}{partial h_{t}}+sumlimits_{t=1}^{T}frac{partial l_{t}}{partial h_{t+1}}frac{partial h_{t+1}}{partial h_{t}}\ & = frac{partial l_{t}}{partial o_{t}}frac{partial o_{t}}{partial h_{t}}+delta_{t+1}frac{partial h_{t+1}}{partial h_{t}}\ end{aligned} δt=∂ht∂L=t=1∑T(∂ot∂lt∂ht∂ot+∂ht+1∂lt∂ht∂ht+1)=∂ot∂lt∂ht∂ot+t=1∑T∂ht+1∂lt∂ht∂ht+1=∂ot∂lt∂ht∂ot+δt+1∂ht∂ht+1
损失对 W W W的偏导数,由于 h t h_{t} ht中含有 h t − 1 h_{t-1} ht−1, h t − 1 h_{t-1} ht−1中也有W,同理 h t − 1 h_{t-1} ht−1中仍然含有 h t − 2 h_{t-2} ht−2,所以损失对 W W W的偏导数要更复杂。具体公式如下: ∂ L ∂ W = ∑ t = 1 T ∂ l t ∂ h t ∂ h t ∂ W = ∑ t = 1 T δ t ( ∂ h t ∂ W + ∂ h t ∂ h t − 1 ∂ h t − 1 ∂ W + ∂ h t ∂ h t − 1 ∂ h t − 1 ∂ h t − 2 ∂ h t − 2 ∂ W + …   ) = ∑ t = 1 T δ t ∑ k = 1 t ( ∏ j = k t − 1 ∂ h j + 1 ∂ h j ) ∂ h k ∂ W begin{aligned} frac{partial L}{partial W} & = sumlimits_{t=1}^{T}frac{partial l_{t}}{partial h_{t}}frac{partial h_{t}}{partial W} \ & = sumlimits_{t=1}^{T}delta_{t}(frac{partial h_{t}}{partial W}+frac{partial h_{t}}{partial h_{t-1}}frac{partial h_{t-1}}{partial W}+frac{partial h_{t}}{partial h_{t-1}}frac{partial h_{t-1}}{partial h_{t-2}}frac{partial h_{t-2}}{partial W}+dots ) \ & = sumlimits_{t=1}^{T}delta_{t}sumlimits_{k=1}^{t}(prodlimits_{j=k}^{t-1}frac{partial h_{j+1}}{partial h_{j}})frac{partial h_{k}}{partial W} end{aligned} ∂W∂L=t=1∑T∂ht∂lt∂W∂ht=t=1∑Tδt(∂W∂ht+∂ht−1∂ht∂W∂ht−1+∂ht−1∂ht∂ht−2∂ht−1∂W∂ht−2+…)=t=1∑Tδtk=1∑t(j=k∏t−1∂hj∂hj+1)∂W∂hk
注意第二个等号的右式,括号中的
∂
h
t
∂
W
frac{partial h_{t}}{partial W}
∂W∂ht,在对
W
W
W求偏导时,
h
t
−
1
h_{t-1}
ht−1看成常数了。损失对
U
U
U和
b
b
b的偏导数如下:
∂
L
∂
U
=
∑
t
=
1
T
∂
l
t
∂
h
t
∂
h
t
∂
U
=
∑
t
=
1
T
δ
t
(
∂
h
t
∂
U
+
∂
h
t
∂
h
t
−
1
∂
h
t
−
1
∂
U
+
∂
h
t
∂
h
t
−
1
∂
h
t
−
1
∂
h
t
−
2
∂
h
t
−
2
∂
U
+
…
 
)
=
∑
t
=
1
T
δ
t
∑
k
=
1
t
(
∏
j
=
k
t
−
1
∂
h
j
+
1
∂
h
j
)
∂
h
k
∂
U
begin{aligned} frac{partial L}{partial U} & = sumlimits_{t=1}^{T}frac{partial l_{t}}{partial h_{t}}frac{partial h_{t}}{partial U} \ & = sumlimits_{t=1}^{T}delta_{t}(frac{partial h_{t}}{partial U}+frac{partial h_{t}}{partial h_{t-1}}frac{partial h_{t-1}}{partial U}+frac{partial h_{t}}{partial h_{t-1}}frac{partial h_{t-1}}{partial h_{t-2}}frac{partial h_{t-2}}{partial U}+dots ) \ & = sumlimits_{t=1}^{T}delta_{t}sumlimits_{k=1}^{t}(prodlimits_{j=k}^{t-1}frac{partial h_{j+1}}{partial h_{j}})frac{partial h_{k}}{partial U} end{aligned}
∂U∂L=t=1∑T∂ht∂lt∂U∂ht=t=1∑Tδt(∂U∂ht+∂ht−1∂ht∂U∂ht−1+∂ht−1∂ht∂ht−2∂ht−1∂U∂ht−2+…)=t=1∑Tδtk=1∑t(j=k∏t−1∂hj∂hj+1)∂U∂hk
∂ L ∂ b = ∑ t = 1 T ∂ l t ∂ h t ∂ h t ∂ b = ∑ t = 1 T δ t ( ∂ h t ∂ b + ∂ h t ∂ h t − 1 ∂ h t − 1 ∂ b + ∂ h t ∂ h t − 1 ∂ h t − 1 ∂ h t − 2 ∂ h t − 2 ∂ b + …   ) = ∑ t = 1 T δ t ∑ k = 1 t ( ∏ j = k t − 1 ∂ h j + 1 ∂ h j ) ∂ h k ∂ b begin{aligned} frac{partial L}{partial b} & = sumlimits_{t=1}^{T}frac{partial l_{t}}{partial h_{t}}frac{partial h_{t}}{partial b} \ & = sumlimits_{t=1}^{T}delta_{t}(frac{partial h_{t}}{partial b}+frac{partial h_{t}}{partial h_{t-1}}frac{partial h_{t-1}}{partial b}+frac{partial h_{t}}{partial h_{t-1}}frac{partial h_{t-1}}{partial h_{t-2}}frac{partial h_{t-2}}{partial b}+dots ) \ & = sumlimits_{t=1}^{T}delta_{t}sumlimits_{k=1}^{t}(prodlimits_{j=k}^{t-1}frac{partial h_{j+1}}{partial h_{j}})frac{partial h_{k}}{partial b} end{aligned} ∂b∂L=t=1∑T∂ht∂lt∂b∂ht=t=1∑Tδt(∂b∂ht+∂ht−1∂ht∂b∂ht−1+∂ht−1∂ht∂ht−2∂ht−1∂b∂ht−2+…)=t=1∑Tδtk=1∑t(j=k∏t−1∂hj∂hj+1)∂b∂hk
RNN的梯度消失问题
同DNN一样,RNN的反向传播公式中含有对激活函数的求导,sigmoid激活函数导数小于等于0.25大于0,tanh的激活函数导数小于等于1大于0,这样就会导致,随着反向传播层数的增加以及反向传播经历时间的变长,我们的误差偏导数会不断的乘以激活函数的导数,进而不断变小,造成RNN不容易对靠近输入 x x x和输入 h h h的参数的更新。
针对这一问题,学者们提出了很多RNN改进形式,最有名的就是LSTM。
长短期记忆网络(LSTM)
长短期记忆模型(long short time memory,简称LSTM)由Schmidhuber等人在1997年提出,与高速公路网络(highway networks)有异曲同工之妙。LSTM主体结构沿用RNN的样子,只是把RNN cell改成了LSTM cell,引入了门控结构和细胞状态的概念,输入门作用于输入信息,遗忘门作用于之前的记忆信息,二者加权和,得到汇总信息,最后通过输出门决定输出信息。
LSTM结构
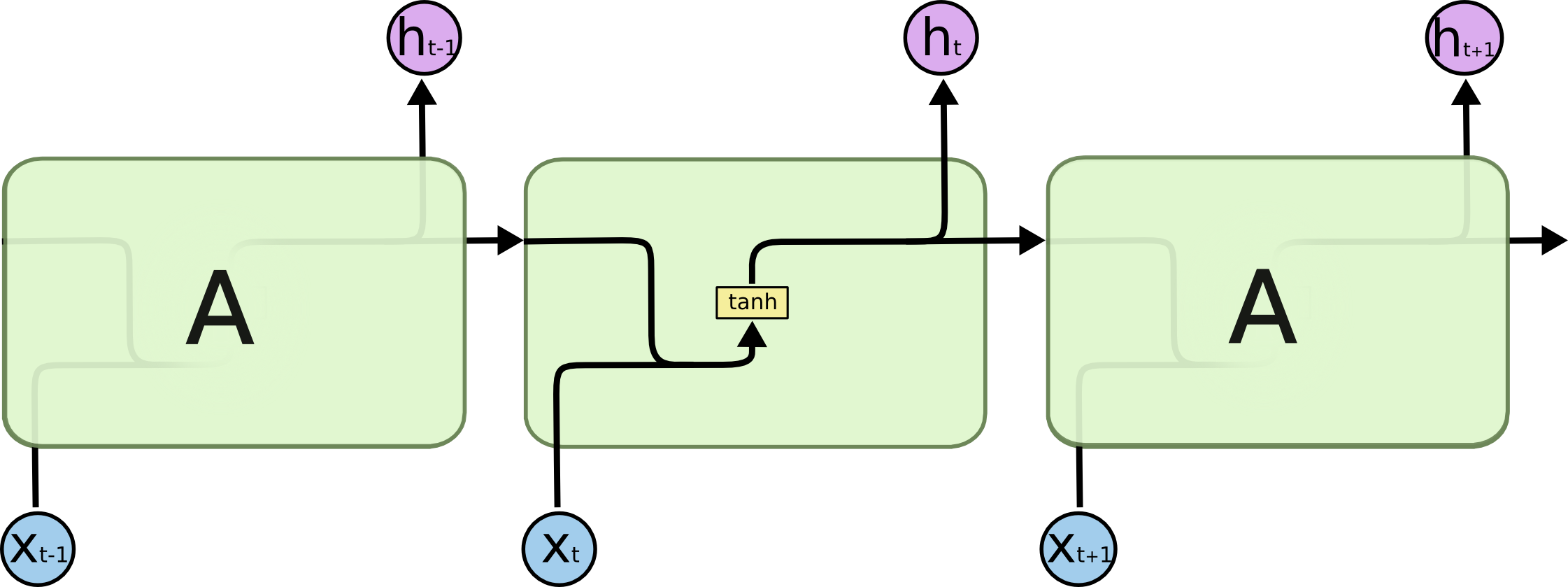
RNN cell可以表示成下图,在该图中激活函数选用的 t a n h tanh tanh。
改进后的LSTM cell有很多种不同的结构,最常见最基本的结构可以表示成下图
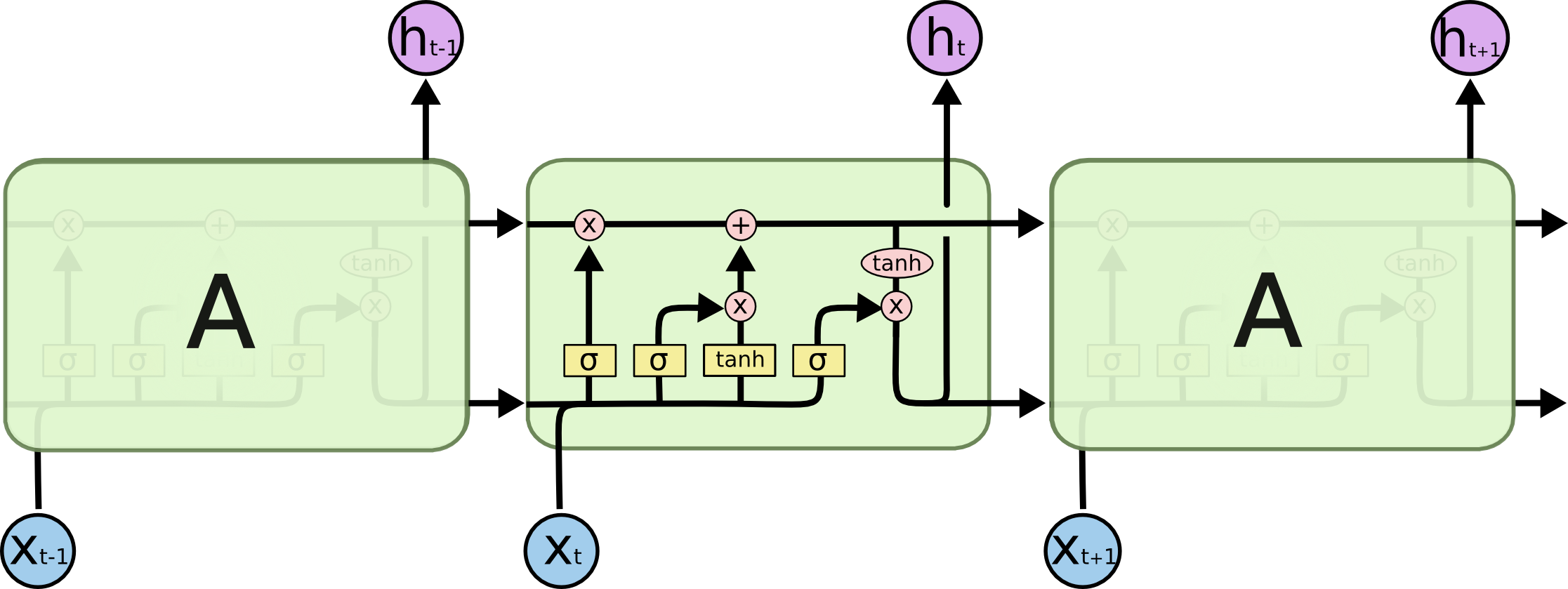
其中,

可见,LSTM的cell结构要更加的复杂,我们可以看到,LSTM相对于RNN中单一的隐藏状态 h h h,还维系了一个更加全局的细胞状态 c c c,具体看下图
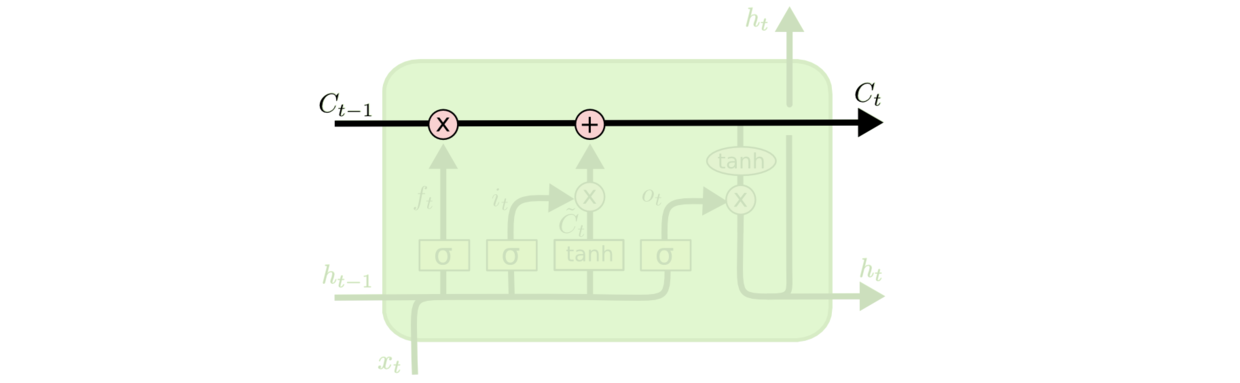
细胞状态也是在隐层内随着时间进行传递,我们可以认为细胞状态就是"主线剧情",或者把LSTM理解成人的大脑,在 t t t时刻,传入的 c t − 1 c_{t-1} ct−1细胞状态就代表大脑在经过前 t − 1 t-1 t−1个cell后记住的东西,在 t t t时刻的cell中,我们会动态忘记(删去)细胞状态中的一些东西,并加上一些新的东西到我们的细胞状态中,更新后的细胞状态在同 h t − 1 h_{t-1} ht−1和 x t x_{t} xt组合后产生 t t t时刻该cell的隐藏层状态 h t h_{t} ht, h t h_{t} ht会传给更深层的cell以及 t + 1 t+1 t+1时刻的cell。这分别就是LSTM中遗忘门,输入门,输出门的作用。注意在cell中传递的都是张量。
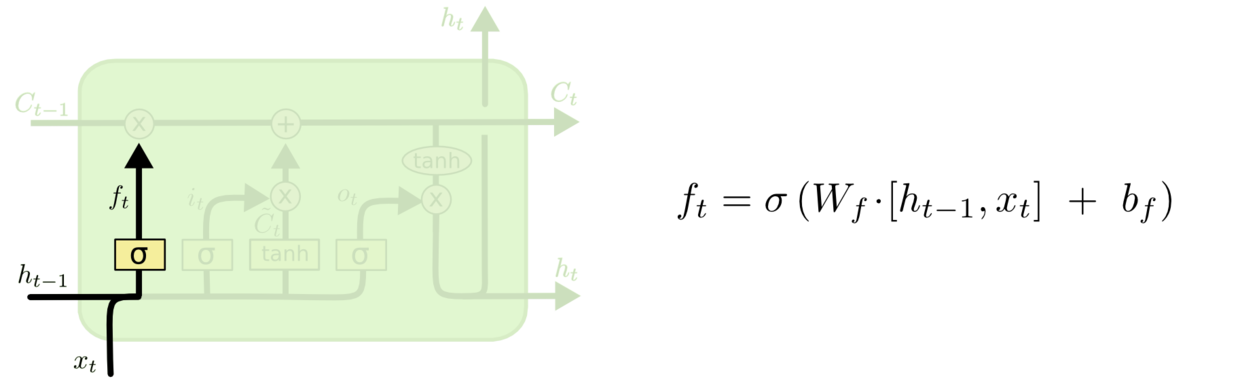
下面给出了LSTM的遗忘门示意图,它根据 h t − 1 h_{t-1} ht−1和 x t x_{t} xt决定忘记细胞状态的哪些值。
下面给出了LSTM的输入门示意图,它根据 h t − 1 h_{t-1} ht−1和 x t x_{t} xt决定,把哪些东西加到细胞状态中。
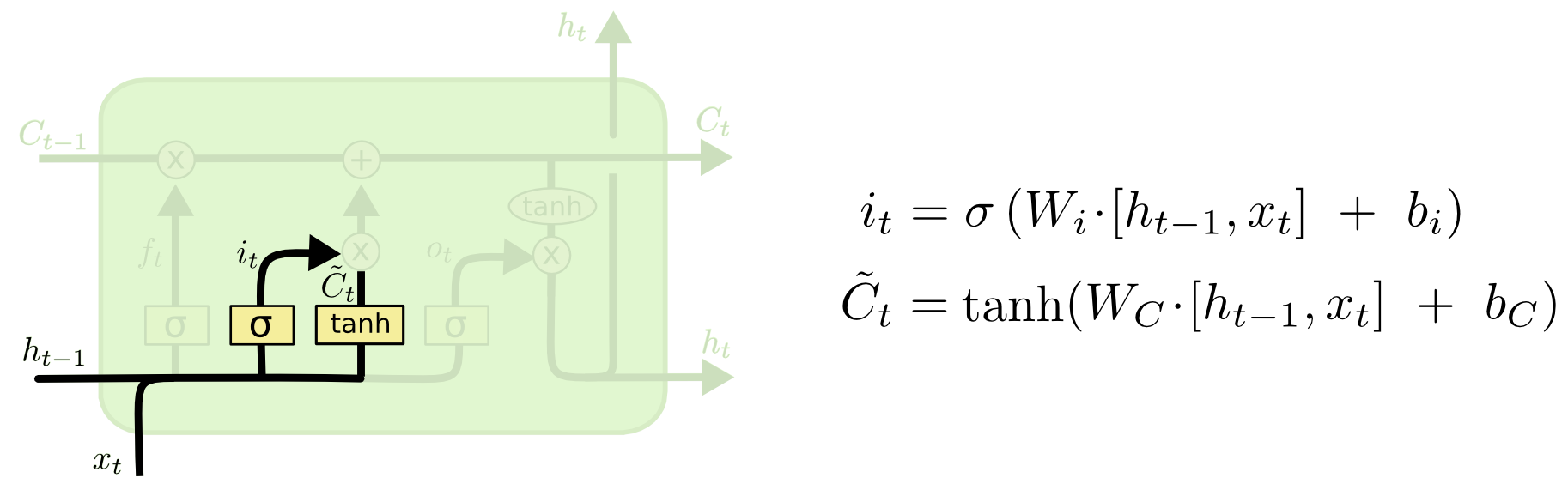
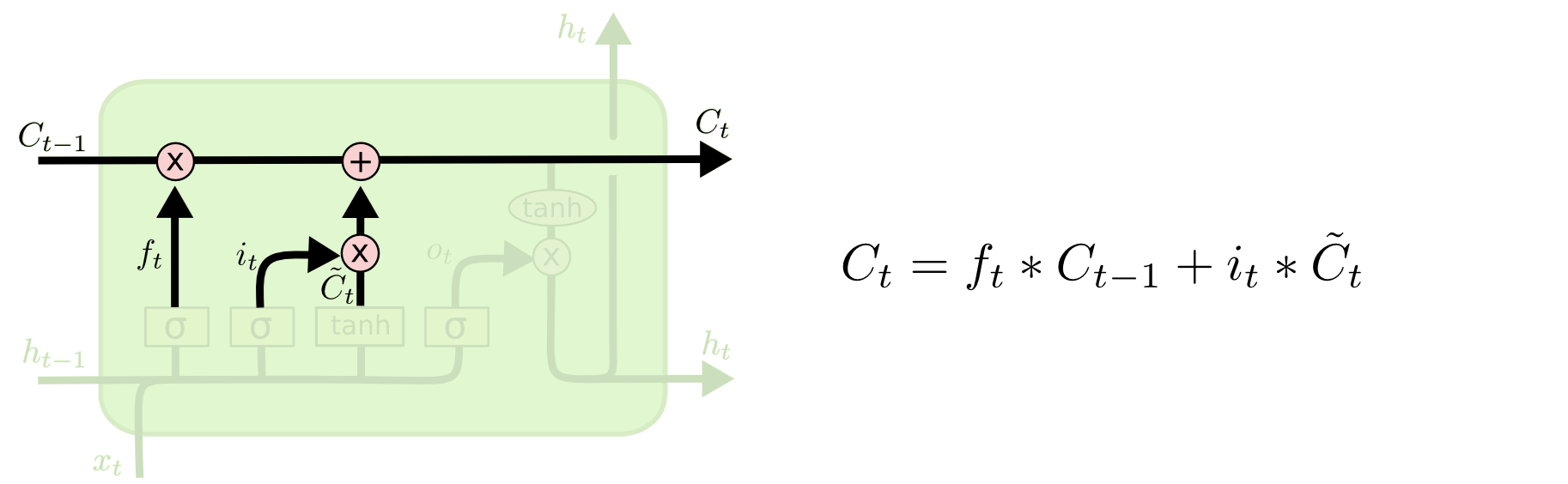
下面给出了LSTM的输入门和遗忘门,是如何作用到细胞状态的示意图,可以看到,遗忘门经过激活函数,是乘在细胞状态上的,如果选用sigmoid激活函数,sigmoid激活函数输出是0,1之间,乘在细胞状态上,就相当于对细胞状态进行了一种"遗忘"操作,其中0表示"完全遗忘"之前 t − 1 t-1 t−1个cell积累的状态值,1表示"完全保留"之前 t − 1 t-1 t−1个cell积累的状态值;而输出门是加在细胞状态上的,就相当于对细胞状态进行了一种"写入"操作。
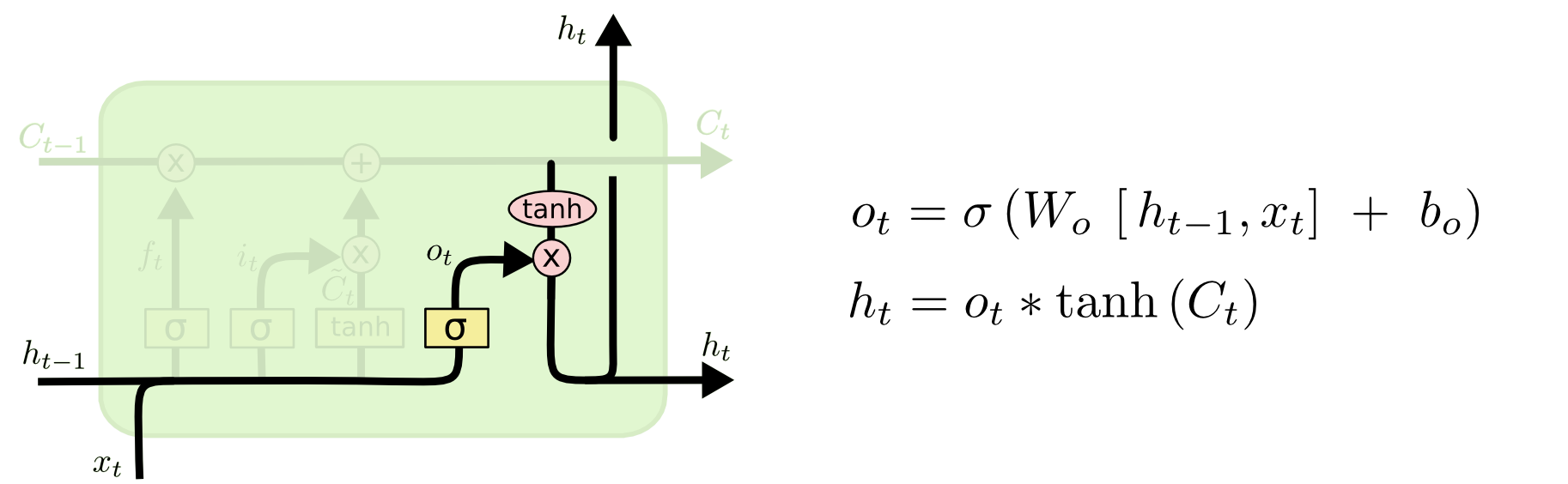
下面给出了LSTM输出门示意图,经过了遗忘门和输入门后的细胞状态,会进一步进行封装,即同 h t − 1 h_{t-1} ht−1和 x t x_{t} xt组合后产生 t t t时刻该cell的隐藏层状态 h t h_{t} ht, h t h_{t} ht会传给更深层的cell以及 t + 1 t+1 t+1时刻的cell。
第一次看到LSTM的结构时,就被这样的门控结构惊呆了,果然是大神设计出的神经网络结构,个人理解,由于细胞状态是贯穿整个隐层的所有cell的,所以一定程度上缓解了梯度消失问题。但还不是很能理解,在输入门和输出门中为何要设计成双激活函数相乘的结构,不是很清楚这样设计的目的何在。
用三种门结构解释LSTM是目前很多blog用的方法,其实LSTM还可以用五种门结构来理解,新加入了输入调制门(input modulation gate)和输出调制门(output modulation gate),结构其实还是一样的,只不过用五门结构解释会更加的具体,见下图:
不难看出,输入调制和输出调制都是针对最中间的细胞状态说的。
LSTM反向传播
这一部分可以看刘建平老师关于LSTM反向传播的推导,过程还是很复杂的。
LSTM神经元个数
LSTM的神经元的看待方式,同上面RNN的神经元看待方式是一样。
参考资料:
RNN:https://www.cnblogs.com/pinard/p/6509630.html
LSTM:https://www.cnblogs.com/pinard/p/6519110.html
RNN+LSTM:https://blog.csdn.net/zhaojc1995/article/details/80572098
根据输入输出对RNN进行分类:https://blog.csdn.net/qq_38742161/article/details/87560232
循环神经网络:https://mp.weixin.qq.com/s?__biz=MzU4MjQ3MDkwNA==&mid=2247484310&idx=1&sn=0fc55a2784a894100a1ae64d7dbfa23d&chksm=fdb69e01cac1171758cb021fc8779952e55de41032a66ee5417bd3e826bf703247e243654bd0&scene=21#wechat_redirect
最后
以上就是刻苦画笔最近收集整理的关于循环神经网络(RNN)与长短期记忆网络(LSTM)循环神经网络(RNN)长短期记忆网络(LSTM)的全部内容,更多相关循环神经网络(RNN)与长短期记忆网络(LSTM)循环神经网络(RNN)长短期记忆网络(LSTM)内容请搜索靠谱客的其他文章。








发表评论 取消回复